Câu hỏi:
11/10/2024 1,854Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC)
và SA = a. Đáy ABC thỏa mãn AB = (tham khảo hình vẽ).
Tìm số đo góc giữa đường thẳng SB và mặt phẳng (ABC).
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
* Phương pháp giải:
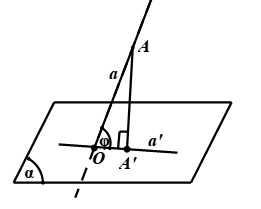
Để xác định góc giữa đường thẳng a và mặt phẳng (α) ta thực hiện theo các bước sau:
+ Bước 1: Tìm giao điểm O của đường thẳng a và (α)
+ Bước 2: Dựng hình chiếu A’ của một điểm A ∈ a xuống (α)
+ Bước 3: Góc ∠AOA' = φ chính là góc giữa đường thẳng a và (α)
Lưu ý:
- Để dựng hình chiếu A’ của điểm A trên (α) ta chọn một đường thẳng b ⊥ (α) khi đó AA’ // b.
- Để tính góc φ ta sử dụng hệ thức lượng trong tam giác vuông OAA’.
* Lời giải:
* Một số lý thuyết liên quan:
Cách tính góc giữa đường thẳng và mặt phẳng
Dạng 1: Góc giữa cạnh bên và mặt đáy
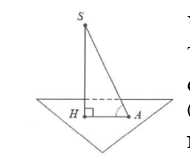
Tìm góc giữa cạnh bên SA và mặt đáy (ABC)
Gọi H là hình chiếu vuông góc của S trên mặt phẳng đáy (ABC).
Như vậy HA là hình chiếu vuông góc của SA trên (ABC).
Vậy
Dạng 2: Góc giữa cạnh bên và mặt phẳng chứa đường cao

Tìm góc giữa cạnh bên SB và mặt phẳng (SHA) với
Dựng , có
Suy ra K là hình chiếu vuông góc của B trên mặt phẳng (SAH).
Vậy
Dạng 3: Góc giữa đường cao và mặt bên
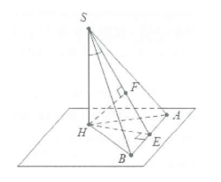
Tìm góc giữa đường cao SH và mặt phẳng (SAB).
Dựng
Ta có:
Mặt khác là hình chiếu vuông góc của H trên mặt phẳng (SAB).
Vậy
Ta có công thức:
Từ đó suy ra các giá trị hoặc nếu đề bài yêu cầu.
Xem thêm các bài viết liên quan hay, chi tiết:
100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1)
Góc giữa đường thẳng và mặt phẳng (lý thuyết, công thức) các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án 2023) – Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và AB = , AC = , CCD = a. Gọi E là trung tâm của AC (tham khảo hình vẽ bên). Góc giữa đường thẳng AB và DE bằng
Câu 2:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với
nhau và OA = a, OB = 2a, OC = 3a. Thể tích của khối tứ
diện OABC bằng
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a,
BC =2a, đường thẳng SA vuông góc với mặt phẳng (ABCD) và
SA =3a . Thể tích của khối chóp S.ABCD bằng
Câu 4:
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm
A', B', C' sao cho SA' = SA , SB' = SB, SC' = SC. Gọi V và V'
lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số là
Câu 5:
Cho tam giác ABCvuông cân tại A, AB = 2a . Thể tích của khối
tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AB bằng
Câu 6:
Cho hình chóp tam giác đều S.ABC có cạnh AB = a,
góc tạo bởi (SAB) và (ABC) bằng 60o. Diện tích xung
quanh của hình nón đỉnh S và có đường tròn đáy ngoại
tiếp tam giác ABC bằng
Câu 7:
Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc
với nhau từng đôi một (như hình vẽ bên dưới). Khẳng định
nào sau đây sai?
Câu 8:
Hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a.
Tam giác SAB vuông cân tại S và tam giác SCD đều. Tính bán
kính mặt cầu ngoài tiếp hình chóp S.ABCD.
Câu 9:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, gọi I là trung điểm của AB, hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của CI, góc giữa SA và mặt đáy bằng (tham khảo hình vẽ bên dưới). Khoảng cách giữa 2 đường thẳng SA và CI bằng:
Câu 10:
Cho hình lăng trụ đều ABC.A’B’C’. Biết khoảng cách từ điểm C
đến mặt phẳng (ABC’) bằng a, góc giữa 2 mặt phẳng (ABC’) và
(BCC’B’) bằng a với cos (tham khảo hình vẽ dưới đây). Thể
tích khối lăng trụ ABC.A’B’C’ bằng
Câu 11:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a,
cạnh bên SA = , mặt bên SAB là tam giác cân đỉnh S và
thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách
giữa hai đường thẳng AD và SC bằng
Câu 12:
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng
(ABC) và SA = a. Đáy ABC nội tiếp trong đường tròn
tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính
bán kính mặt cầu ngoại tiếp khối chóp S.ABC
Câu 13:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc tạo bởi SA và CD.
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
cạnh bên SD = . Hình chiếu vuông góc của S trên mặt phẳng
(ABCD) là điểm H thuộc đoạn BD sao cho = -3. Gọi M là
trung điểm của cạnh SD. Tính khoảng cách giữa hai đường thẳng
CM và SB.
Câu 15:
Tính thể tích của khối nón tròn xoay có chiều cao bằng 6 và đường kính đường tròn đáy bằng 16.