Câu hỏi:
17/06/2026 277
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD.
a) Tìm các giao tuyến: d1 = (SAB) ∩ (SCD); d2 = (SCD) ∩ (MAB).
b) Chứng minh d1 // d2.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD.
a) Tìm các giao tuyến: d1 = (SAB) ∩ (SCD); d2 = (SCD) ∩ (MAB).
b) Chứng minh d1 // d2.
Trả lời:
Giải bởi Vietjack
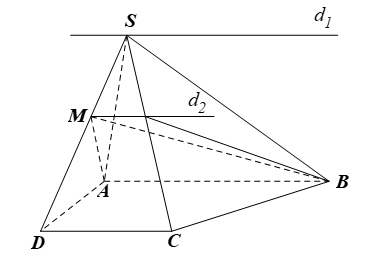
a) • S ∈ (SAD) và S ∈ (SBC) nên S ∈ (SAB) ∩ (SDC).
Mặt khác có AB ⊂ (SAB), CD ⊂ (SDC) và AB // CD (do ABCD là hình thang)
Suy ra (SAB) ∩ (SCD) = d1 với d1 là đường thẳng đi qua S và d1 // AB // CD.
• Ta có M ∈ SD, mà SD ∈ (SCD) nên M ∈ (SCD)
Lại có M ∈ (MAB)
Suy ra (SCD) ∩ (MAB) = M
Mặt khác có AB ⊂ (MAB), CD ⊂ (SCD) và AB // CD
Suy ra (SCD) ∩ (MAB) = d2 với d2 là đường thẳng đi qua M và d2 // AB // CD.
b) Theo câu a, ta có d1 // AB // CD và d2 // AB // CD
Suy ra d1 // d2.
a) • S ∈ (SAD) và S ∈ (SBC) nên S ∈ (SAB) ∩ (SDC).
Mặt khác có AB ⊂ (SAB), CD ⊂ (SDC) và AB // CD (do ABCD là hình thang)
Suy ra (SAB) ∩ (SCD) = d1 với d1 là đường thẳng đi qua S và d1 // AB // CD.
• Ta có M ∈ SD, mà SD ∈ (SCD) nên M ∈ (SCD)
Lại có M ∈ (MAB)
Suy ra (SCD) ∩ (MAB) = M
Mặt khác có AB ⊂ (MAB), CD ⊂ (SCD) và AB // CD
Suy ra (SCD) ∩ (MAB) = d2 với d2 là đường thẳng đi qua M và d2 // AB // CD.
b) Theo câu a, ta có d1 // AB // CD và d2 // AB // CD
Suy ra d1 // d2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:
a) (SAD) và (SBC);
b) (SAB) và (MDC), với M là một điểm bất kì thuộc cạnh SA.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:
a) (SAD) và (SBC);
b) (SAB) và (MDC), với M là một điểm bất kì thuộc cạnh SA.
Câu 2:
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho I; J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN // BC.
b) Tứ giác MNJI là hình gì. Tìm điểu kiện để tứ giác MNJI là hình bình hành.
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho I; J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN // BC.
b) Tứ giác MNJI là hình gì. Tìm điểu kiện để tứ giác MNJI là hình bình hành.
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q.
a) Chứng minh MN song song với PQ.
b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q.
a) Chứng minh MN song song với PQ.
b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.
