Câu hỏi:
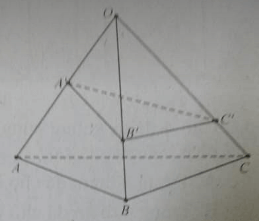
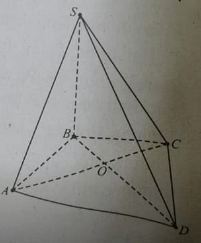
22/07/2024 183Cho hình chóp O.ABC, A’ là trung điểm của OA; các điểm B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng.
A. Giao tuyến của (OBC) và (A’B’C’) là A’B’;
B. Giao tuyến của (ABC) và (OC’A’) là CK, với K là giao điểm của C’B’ với CB
C. (ABC) và (A’B’C’) không cắt nhau
D. Giao tuyến của (ABC) và (A’B’C’) là MN, với M là giao điểm của AC và A’C’, N là giao điểm của BC và B’C’.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
* Phương án A sai vì A’ không phải là điểm chung của (OBC) và (A’B’C’).
* Phương án B sai vì
Xét giao tuyến của 2 mp (ABC ) và (OC'A') có:
A chung
C chung
Do đó, giao tuyến của mp(ABC) và mp (OC'A') là AC
+ Phương án C sai vì:
Trong mp (OAB), A’B’ không song song với AB nên sẽ cắt AB, do vậy (ABC) và (A’B’C’) có điểm chung
+ Phương án D đúng vì M là giao điểm của AC và A’C’ nên M là điểm chung của (ABC) và (A’B’C’),
Tương tự N là điểm chung của (ABC) và (A’B’C’).
Vì vậy MN là giao tuyến của (ABC) và (A’B’C’).
Chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
Câu 8:
Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
Câu 10:
Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?
Câu 11:
Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
Câu 12:
Cho 6 đường thẳng đôi một cắt nhau. Hỏi xác định được nhiểu nhất bao nhiêu mặt phẳng đi qua 2 trong số các đường thẳng đã cho
Câu 13:
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
Hình vẽ như sau:
Câu 14:
Cho hình chóp S.ABCD, các điểm A’, B’, C’ lần lượt thuộc các cạnh SA, SB, SC. Phát biểu nào sau đây là đúng?
Câu 15:
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?