Câu hỏi:
13/07/2024 125
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
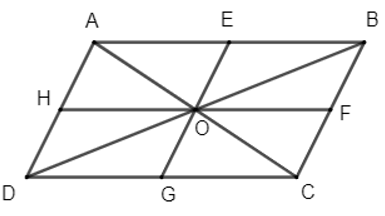
a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và OE = BC (1).
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và OG = BC (2).
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).

a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và OE = BC (1).
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và OG = BC (2).
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Câu 2:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ
Câu 3:
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Câu 4:
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.
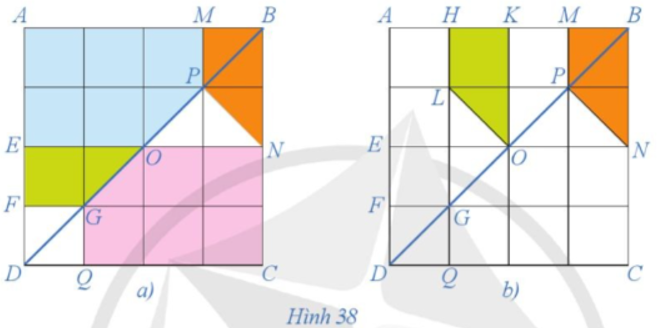
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.

Câu 6:
Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.
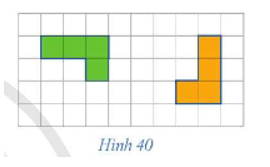
Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.

Câu 7:
Hình 41 là hình viên gạch men.
a) Xác định tâm đối xứng của viên gạch.
b) Xác định các trục đối xứng của viên gạch.
c) Xác định ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay φ = 90°.

Hình 41 là hình viên gạch men.
a) Xác định tâm đối xứng của viên gạch.
b) Xác định các trục đối xứng của viên gạch.
c) Xác định ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay φ = 90°.

Câu 8:
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2).
b) Tìm phép đối xứng tâm biến đường tròn (O1) thành đường tròn (O2).
c) Tìm phép đối xứng trục biến đường tròn (O1) thành đường tròn (O2).
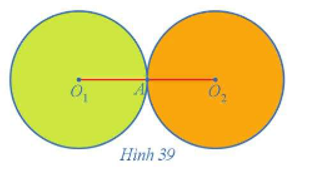
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2).
b) Tìm phép đối xứng tâm biến đường tròn (O1) thành đường tròn (O2).
c) Tìm phép đối xứng trục biến đường tròn (O1) thành đường tròn (O2).

Câu 9:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(– 3; 2) bán kính R = 1. Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ . Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(– 3; 2) bán kính R = 1. Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ . Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
Câu 10:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ .
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ .
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Câu 12:
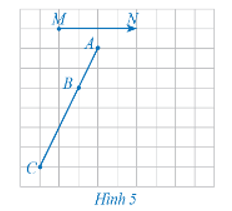
Xét phép tịnh tiến theo vectơ (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Xét phép tịnh tiến theo vectơ (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.

Câu 13:
Cho vectơ và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho (Hình 3).
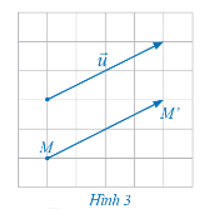
Cho vectơ và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho (Hình 3).

Câu 14:
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Xác định một phép dời hình biến:
a) Tam giác AMQ thành tam giác CPN;
b) Tam giác AMO thành tam giác PCN.
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Xác định một phép dời hình biến:
a) Tam giác AMQ thành tam giác CPN;
b) Tam giác AMO thành tam giác PCN.
Câu 15:
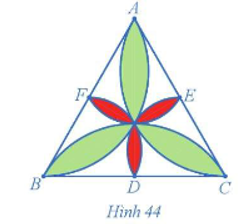
Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
a) Cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.
Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
a) Cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.



