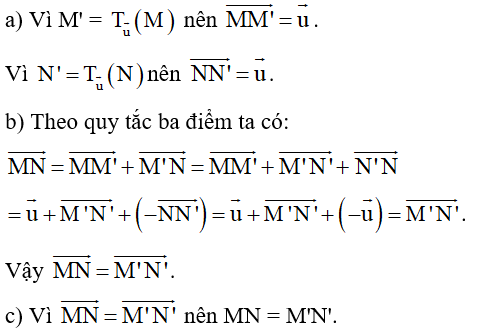Chuyên đề Toán 11 Cánh diều Chuyên đề 1. Phép biến hình phẳng
Chuyên đề Toán 11 Cánh diều Chuyên đề 1. Phép biến hình phẳng
-
248 lượt thi
-
44 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Thang băng chuyền tải khách (Hình 1) là loại thang máy không có bậc thang, tốc độ di chuyển vừa phải, thường được sử dụng ở những nơi công cộng như khu trung tâm thương mại, sân bay, siêu thị, ... nhằm mục đích hỗ trợ hành khách di chuyển từ địa điểm này đến địa điểm khác cùng với đồ đạc, hành lí, ...
Giả sử thang băng chuyền di chuyển một hành khách từ điểm đầu A đến điểm cuối B của thang băng chuyền đó.
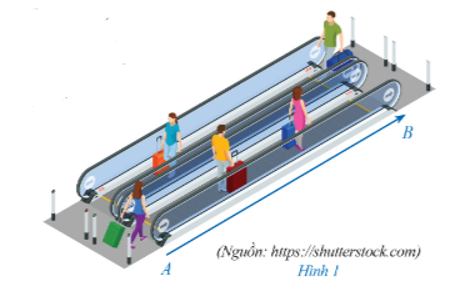
Trong toán học, phép di chuyển hành khách từ vị trí A đến vị trí B theo một hướng cố định được gọi là gì?
 Xem đáp án
Xem đáp án
Trong toán học, phép di chuyển hành khách từ vị trí A đến vị trí B theo một hướng cố định được gọi là phép dời hình.
Câu 2:
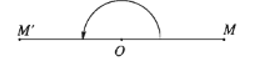
13/07/2024Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc M' của điểm M lên đường thẳng d (Hình 2).
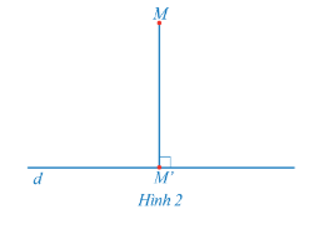
a) Có bao nhiêu hình chiếu vuông góc của điểm M trên đường thẳng d?
b) Có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d hay không?
 Xem đáp án
Xem đáp án
a) Với mỗi điểm M có một điểm M' duy nhất là hình chiếu vuông góc của điểm M trên đường thẳng d cho trước.
b) Không có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d.
Câu 3:
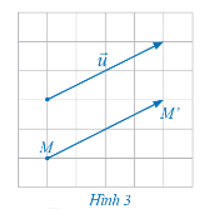
11/07/2024Cho vectơ và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho (Hình 3).
 Xem đáp án
Xem đáp án
Cách xác định điểm M' trong mặt phẳng sao cho :
- Qua M kẻ đường thẳng d song song với giá của vectơ (hoặc trùng với giá của vectơ nếu điểm M thuộc giá của vectơ ).
- Trên đường thẳng d, lấy điểm M' sao cho MM' = , và hướng từ M đến M' cùng hướng với vectơ . (Tham khảo Hình 3)
Câu 7:
18/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ .
 Xem đáp án
Xem đáp án
Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ là một đường tròn bán kính bằng 3, gọi là (C').
Gọi O' là tâm của (C'). Ta có O' là ảnh của O qua phép tịnh tiến theo vectơ nên . Suy ra O'(3; 4).
Vậy ảnh của đường tròn (C) là đường tròn (C') có tâm O'(3; 4), bán kính bằng 3.
Câu 8:
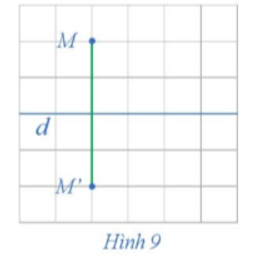
23/07/2024Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
 Xem đáp án
Xem đáp án
Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM':
- Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H.
- Trên d', lấy điểm M' sao cho MH = M'H.
Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'.
Câu 9:
23/07/2024Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
 Xem đáp án
Xem đáp án
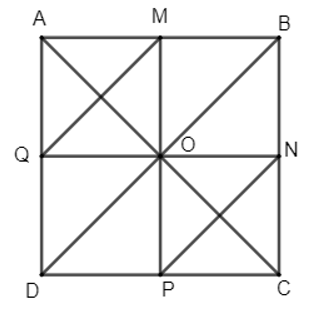
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.
Câu 10:
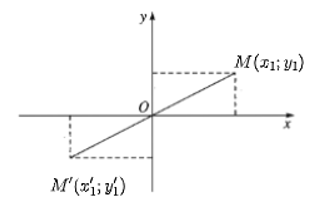
15/07/2024Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
 Xem đáp án
Xem đáp án
a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì .
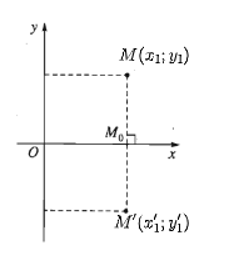
Do đó M'(x1; – y1) và N'(x2; – y2).
b) Ta có: ;
.Câu 11:
16/07/2024Xét phép đối xứng trục d (Hình 11).
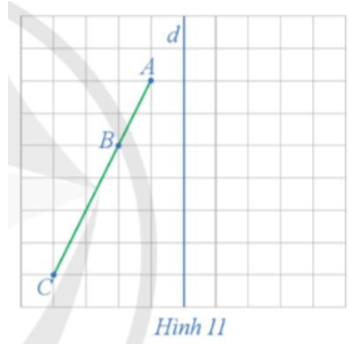
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
 Xem đáp án
Xem đáp án
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
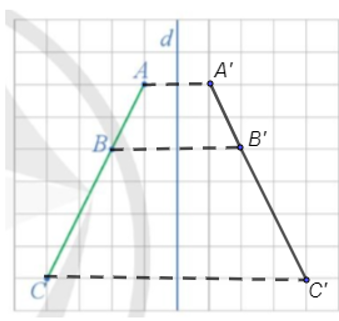
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Câu 12:
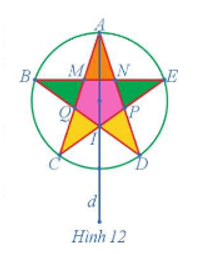
05/07/2024Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
 Xem đáp án
Xem đáp án
Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q.
Câu 13:
22/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
 Xem đáp án
Xem đáp án
Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2.
Câu 14:
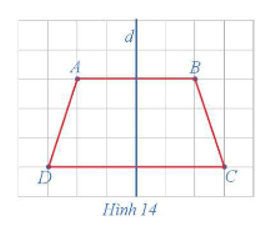
07/07/2024Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
 Xem đáp án
Xem đáp án
Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD.
Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d.
Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
Câu 15:
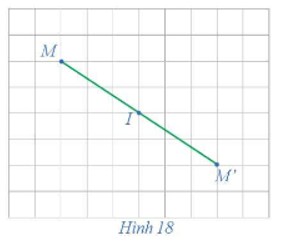
21/07/2024Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).
 Xem đáp án
Xem đáp án
Cách xác định:
Lấy điểm I trong mặt phẳng, với mỗi điểm M bất kì, ta vẽ đường thẳng MI, trên đường thẳng này, ta lấy điểm M' sao cho MI = M'I và điểm I nằm giữa hai điểm M và M'. Khi đó I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I).
Câu 16:
22/07/2024Cho bát giác đều ABCDEGHK với tâm I. Xác định ảnh của các điểm A, B, C, D qua phép đối xứng tâm I.
 Xem đáp án
Xem đáp án
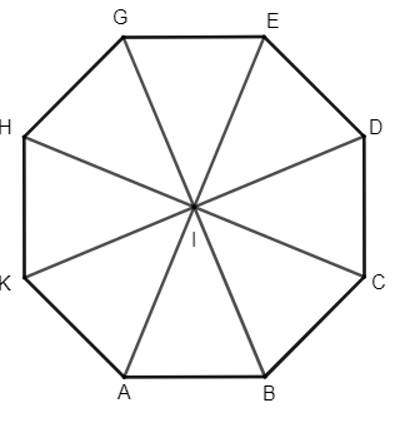
Vì I là tâm của bát giác đều ABCDEGHK nên I là trung điểm của các đoạn thẳng AE, BG, CH, DK. Suy ra ảnh của các điểm A, B, C, D qua phép đối xứng tâm I lần lượt là các điểm E, G, H, K.
Câu 17:
18/07/2024Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng tâm O.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
 Xem đáp án
Xem đáp án
a) Trong mặt phẳng tọa độ Oxy, điểm M'(x1'; y1') là ảnh của điểm M(x1; y1) qua phép đối xứng tâm O, khi đó .
Do đó, M'(– x1; – y1) và N'(– x2; – y2).
b) Ta có: ;
.
Từ đó suy ra MN = M'N'.
Câu 18:
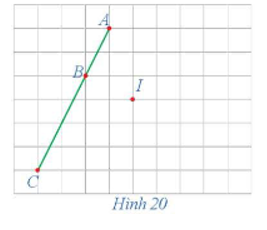
12/07/2024Xét phép đối xứng tâm I (Hình 20).
a) Xác định các điểm A', B', C' là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
 Xem đáp án
Xem đáp án
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I như trên hình vẽ dưới đây.
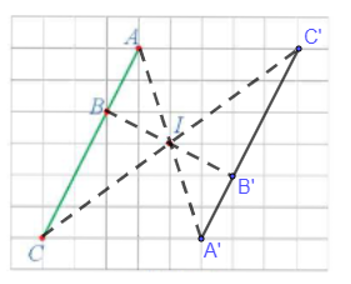
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Câu 19:
21/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1).
 Xem đáp án
Xem đáp án
Ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của điểm I qua phép đối xứng tâm S(2; 1). Suy ra S là trung điểm của II'. Do đó nên I'(2; – 1).
Vậy ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là đường tròn (C') có tâm I'(2;– 1) và bán kính R' = 2.
Câu 20:
06/07/2024Trong mặt phẳng, cho hình tròn tâm O, kí hiệu là ℋ (Hình 22). Xét phép đối xứng tâm ĐO. Tìm ℋ' = ĐO(ℋ).
 Xem đáp án
Xem đáp án
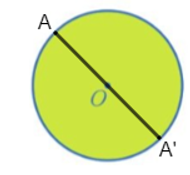
Với mỗi điểm A bất kì thuộc đường tròn tâm O, gọi A' là ảnh của A qua phép đối xứng tâm O. Khi đó O là trung điểm của AA' nên AA' là đường kính của đường tròn tâm O, suy ra A' thuộc đường tròn tâm O.
Như vậy, với mỗi điểm bất kì thuộc đường tròn tâm O, ta đều có ảnh của nó qua phép đối xứng tâm O là một điểm cũng thuộc đường tròn tâm O. Do đó, phép đối xứng tâm O biến đường tròn tâm O thành đường tròn tâm O.
Vậy phép đối xứng tâm O viến hình ℋ thành chính nó hay ℋ ' ≡ ℋ.
Câu 21:
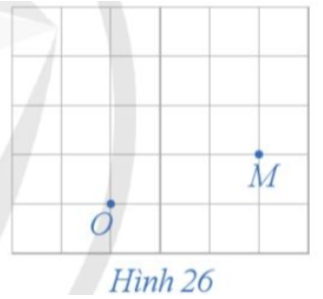
29/06/2024Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
 Xem đáp án
Xem đáp án
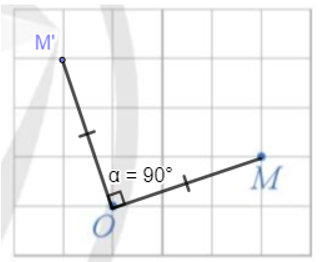
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
Câu 22:
19/07/2024Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
 Xem đáp án
Xem đáp án

Ta có tam giác ABC đều có O là trọng tâm nên và OA = OB = OC. Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
Câu 23:
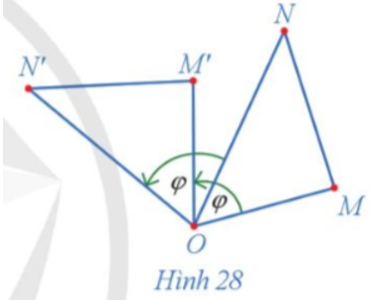
23/07/2024Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
 Xem đáp án
Xem đáp án
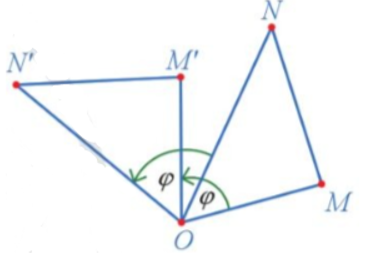
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ nên OM = OM', ON = ON'.
Ta có: và .
Suy ra .
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
(cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ ∆OM'N' = ∆OMN, suy ra M'N' = MN (hai cạnh tương ứng).
Câu 24:
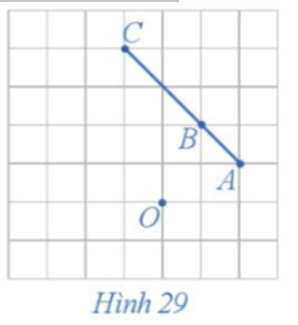
20/07/2024Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
 Xem đáp án
Xem đáp án
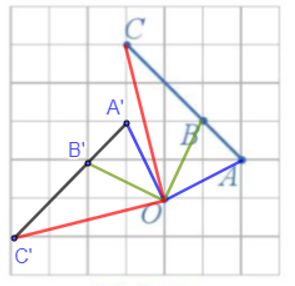
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
Câu 25:
10/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
 Xem đáp án
Xem đáp án
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).

Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Câu 26:
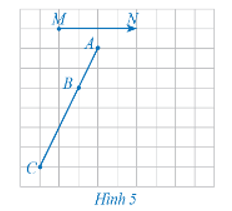
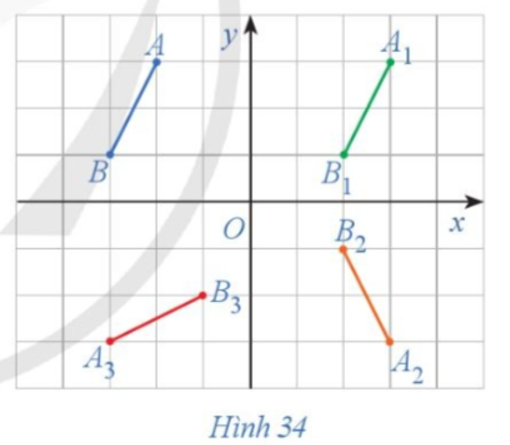
19/07/2024Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ ;
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox;
c) Đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay φ = – 90°;
d) So sánh độ dài các đoạn thẳng AB, A1B1, A2B2, A3B3.
 Xem đáp án
Xem đáp án
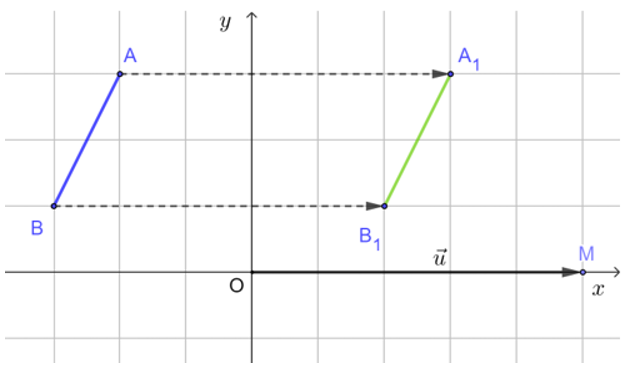
a) Lấy điểm M, sao cho M(5; 0). Khi đó .
Lấy các điểm A1 và B1 sao cho và . Khi đó nên A1, B1 lần lượt là ảnh của A, B qua phép tịnh tiến theo vectơ . Vậy đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ .
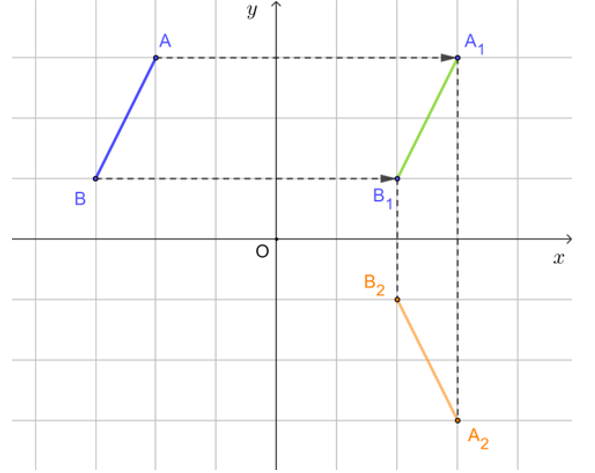
b) Từ A1, kẻ đường thẳng vuông góc với Ox, trên đường thẳng này lấy A2 khác phía với A1 đối với Ox sao cho khoảng cách từ A1 đến Ox bằng khoảng cách từ A2 tới Ox. Khi đó Ox là đường trung trực của đoạn thẳng A1A2.
Tương tự, dựng B2 sao cho Ox là đường trung trực của đoạn thẳng B1B2.
Khi đó ta có phép đối xứng trục Ox biến các điểm A1, B1 tương ứng thành các điểm A2, B2. Vậy đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox.
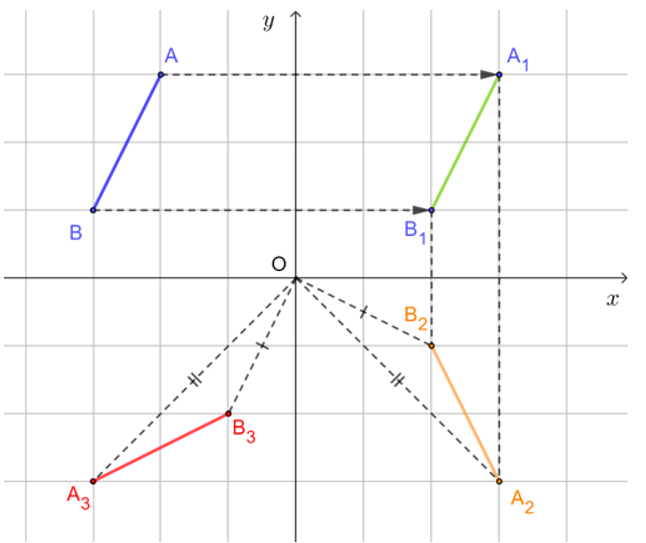
c) Phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.
Qua O, vẽ đường thẳng vuông góc với OA2, trên đường thẳng này lấy điểm A3 sao cho OA2 = OA3 và góc quay từ A2 đến A3 theo chiều kim đồng hồ. Khi đó A3 là ảnh của điểm A2 qua phép quay tâm O, góc quay – 90°. Tương tự, xác định được điểm B3 là ảnh của điểm B2 qua phép quay tâm O, góc quay – 90°. Vậy đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay φ = – 90°.
d) Vì phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì nên AB = A1B1.
Vì phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì nên A1B1 = A2B2.
Vì phép quay bảo toàn khoảng cách giữa hai điểm bất kì nên A2B2 = A3B3.
Do đó, AB = A1B1 = A2B2 = A3B3.
Câu 27:
23/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(– 3; 2) bán kính R = 1. Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ . Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
 Xem đáp án
Xem đáp án
Ảnh của đường tròn (C) qua phép đối xứng tâm O là một đường tròn có bán kính bằng 1, gọi là (C').
Gọi I' là tâm của đường tròn (C'), khi đó I' là ảnh của I qua phép đối xứng tâm O. Suy ra I'(3; – 2). Do vậy, đường tròn (C') có tâm I'(3; – 2) và bán kính bằng 1.
Ảnh của đường tròn (C') qua phép tịnh tiến theo vectơ là một đường tròn có bán kính bằng 1, gọi là (C").
Gọi I" là tâm của đường tròn (C"), khi đó I" là ảnh của I' qua phép tịnh tiến theo vectơ , suy ra nên I"(2; 1). Do vậy, đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Vậy ảnh của đường tròn (C) qua phép dời hình f là đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Câu 28:
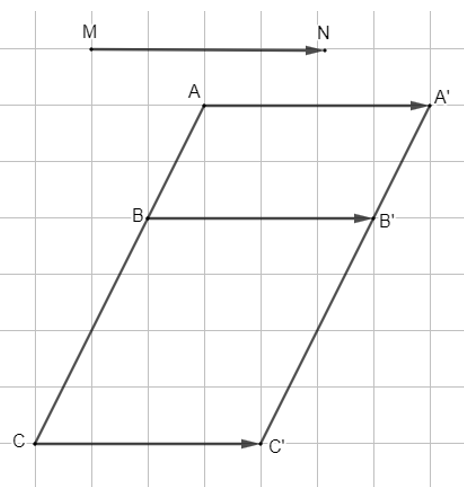
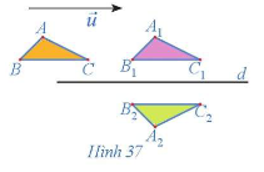
28/06/2024Quan sát Hình 37.
a) Chỉ ra các phép dời hình biến tam giác ABC thành tam giác A1B1C1 và biến tam giác A1B1C1 thành tam giác A2B2C2.
b) Có nhận xét gì về hai tam giác ABC và A2B2C2?
 Xem đáp án
Xem đáp án
a) Quan sát Hình 37, ta thấy phép tịnh tiến theo vectơ biến tam giác ABC thành tam giác A1B1C1 và phép đối xứng trục d biến biến tam giác A1B1C1 thành tam giác A2B2C2.
b) Theo tính chất của phép tịnh tiến và phép đối xứng trục, ta suy ra
AB = A1B1 = A2B2, BC = B1C1 = B2C2, AC = A1C1 = A2C2.
Do đó, hai tam giác ABC và A2B2C2 bằng nhau.
Câu 29:
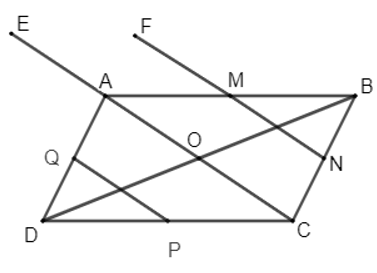
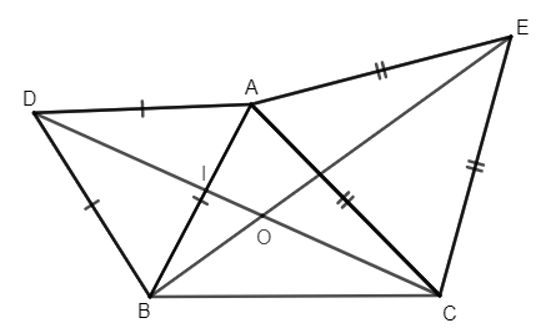
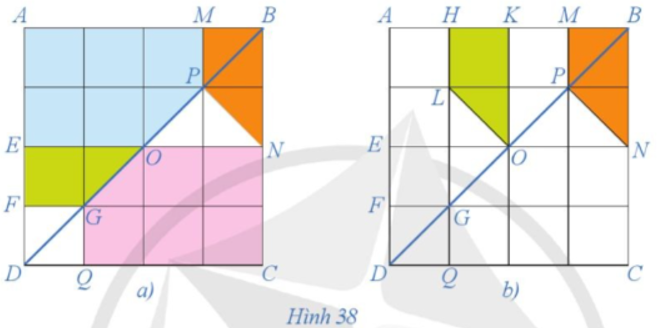
23/07/2024Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.
 Xem đáp án
Xem đáp án
Quan sát hình ta thấy OA = OC, OM = OQ, OP = OG, OE = ON nên O là trung điểm của các đoạn thẳng AC, MQ, PG, EN. Do đó, ta có phép đối xứng tâm O biến các điểm A, M, P, O, E tương ứng thành các điểm C, Q, G, O, N. Như vậy, phép đối xứng tâm O biến hình AMPOE thành hình CQGON. Vậy hai hình AMPOE và CQGON bằng nhau.
Câu 30:
17/07/2024Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
 Xem đáp án
Xem đáp án
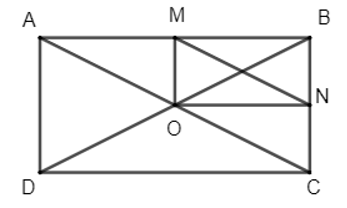
Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC.
Suy ra (1).
Ta có M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = . Do đó, (2).
Từ (1) và (2) suy ra .
Khi đó, ta có phép tịnh tiến theo vectơ biến các điểm A, M, O lần lượt thành các điểm O, N, C.
Vậy phép tịnh tiến theo vectơ biến tam giác AMO thành tam giác ONC.
Câu 31:
18/07/2024Phép đối xứng tâm có là phép quay hay không? Vì sao?
 Xem đáp án
Xem đáp án
Phép đối xứng tâm là phép quay.
Thật vậy, cho điểm O, với mỗi điểm M, ta có M' là ảnh của điểm M qua phép đối xứng tâm O khi O là trung điểm của đoạn thẳng MM', suy ra OM = OM' và .
Khi đó góc lượng giác (OM; OM') có số đo bằng (2k + 1)π và OM = OM' nên ta có phép quay tâm O, góc quay (2k + 1)π biến điểm M thành điểm M'.
Vậy phép đối xứng tâm O là phép quay Q(O, (2k + 1)π).
Câu 32:
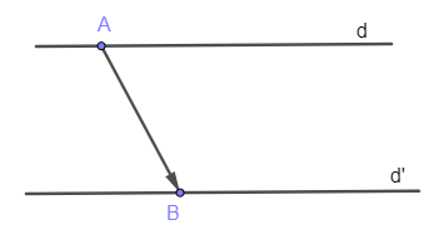
12/07/2024Cho hai đường thẳng d và d' song song với nhau.
a) Chỉ ra một phép tịnh tiến biến d thành d'.
b) Có bao nhiêu phép tịnh tiến biến d thành d'.
 Xem đáp án
Xem đáp án
a) Lấy hai điểm A và B bất kì theo thứ tự thuộc d và d'. Khi đó phép tịnh tiến theo vectơ sẽ biến d thành d'.
b) Vì có vô số cách chọn A ∈ d và B ∈ d' nên có vô số phép tịnh tiến biến d thành d'.
Câu 33:
13/07/2024Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
 Xem đáp án
Xem đáp án
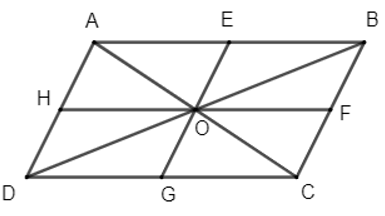
a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và OE = BC (1).
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và OG = BC (2).
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).
Câu 34:
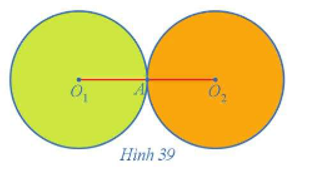
22/07/2024Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2).
b) Tìm phép đối xứng tâm biến đường tròn (O1) thành đường tròn (O2).
c) Tìm phép đối xứng trục biến đường tròn (O1) thành đường tròn (O2).
 Xem đáp án
Xem đáp án
a) Hai đường tròn (O1; R) và (O2; R) có cùng bán kính. Ta có phép tịnh tiến theo vectơ biến điểm tâm O1 thành tâm O2.
Như vậy, phép tịnh tiến theo vectơ biến đường tròn (O1; R) thành đường tròn (O2; R).
b) Ta có: O1A = O2A = R nên A là trung điểm của O1O2. Do đó, có phép đối xứng tâm A biến O1 thành O2.
Như vậy, phép đối xứng tâm O biến đường tròn (O1; R) thành đường tròn (O2; R).
c)
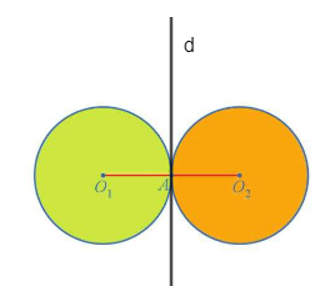
Qua A, kẻ đường thẳng d vuông góc với O1O2. Khi đó đường thẳng d là đường trung trực của đoạn thẳng O1O2. Do đó, ta có phép đối xứng trục d biến O1 thành O2.
Như vậy, phép đối xứng trục d biến đường tròn (O1; R) thành đường tròn (O2; R).
Câu 35:
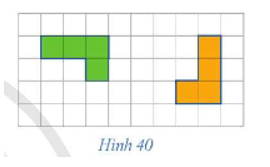
20/07/2024Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.
 Xem đáp án
Xem đáp án
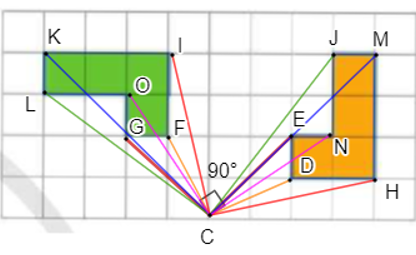
Ta thấy:
+) CH = CI, CM = CK, CJ = CL, CN = CO, CE = CG, CD = CF (đường chéo của các hình chữ nhật có cùng kích thước).
+) .
Do đó, ta có phép quay tâm C, góc quay 90° biến các điểm H, M, J, N, E, D tương ứng thành các điểm I, K, L, O, G, F.
Như vậy, hình màu xanh là ảnh của hình màu cam quay phép quay tâm C, góc quay 90°.
Câu 36:
21/07/2024Hình 41 là hình viên gạch men.
a) Xác định tâm đối xứng của viên gạch.
b) Xác định các trục đối xứng của viên gạch.
c) Xác định ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay φ = 90°.

 Xem đáp án
Xem đáp án
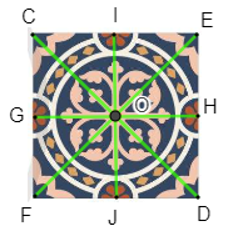
a) Tâm đối xứng của viên gạch là điểm O.
b) Viên gạch có 4 trục đối xứng là các đường thẳng IJ, GH, EF, CD.
c) Viên gạch có dạng hình vuông nên hai đường chéo CD và EF vuông góc với nhau tại tâm đối xứng O và O là trung điểm của mỗi đường chéo nên OE = OC = OF = OD và .
Vì phép quay với góc quay φ = 90° có chiều quay ngược chiều kim đồng hồ.
Do đó, ta có phép quay tâm O, góc quay φ = 90° biến các điểm E, C, F, D tương ứng thành các điểm C, F, D, E.
Từ đó suy ra ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay φ = 90° chính là viên gạch đó.
Câu 37:
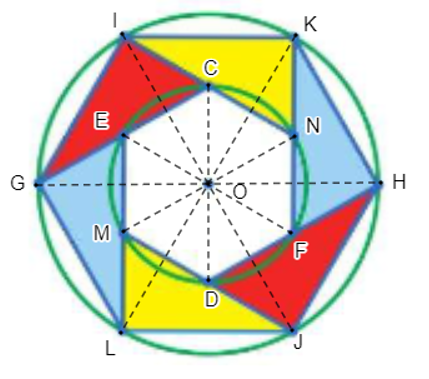
06/07/2024Quan sát Hình 42 và chỉ ra hai phép dời hình (phân biệt) biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
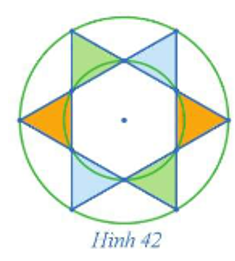
 Xem đáp án
Xem đáp án
+) Đặt các điểm như hình vẽ.
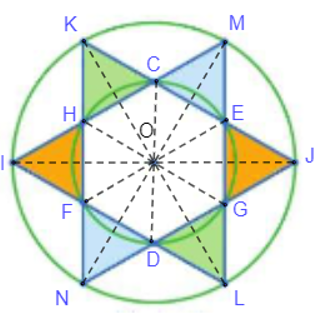
Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, GH nên O là trung điểm của CD, EF, GH. Đường tròn lớn tâm O có các đường kính MN, LK, IJ nên O là trung điểm của MN, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm C, M, E, J, G, L, D tương ứng thành các điểm D, N, F, I, H, K, C.
Từ đó suy ra phép đối xứng tâm O biến các tam giác CME, EJG, GLD, FDN, FHI, KHC tương ứng thành các tam giác DNF, FIH, HKC, ECM, EGJ, LGD hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
+) Đặt các điểm như hình vẽ:
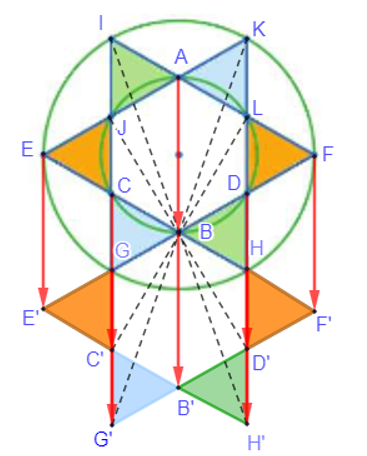
- Phép tịnh tiến theo vectơ biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H'.
- Phép đối xứng tâm B biến các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H' lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI.
Do đó, ta có phép dời hình F có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ và phép đối xứng tâm B ( trước, ĐB sau) biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI hay chính là phép dời hình F đó biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
Câu 38:
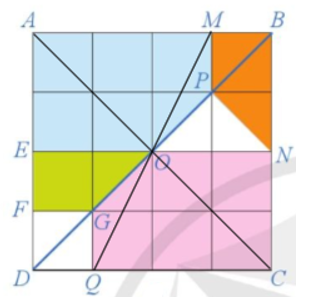
06/07/2024Quan sát Hình 43 và chỉ ra:
a) Một phép dời hình biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Một phép dời hình biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.
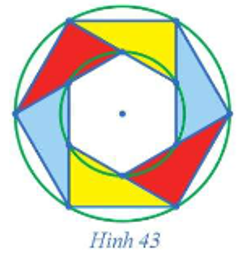
 Xem đáp án
Xem đáp án
Đặt các điểm như hình vẽ.
a) Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, MN nên O là trung điểm của CD, EF, MN. Đường tròn lớn tâm O có các đường kính GH, LK, IJ nên O là trung điểm của GH, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm I, K, N, H, F, D, J tương ứng thành các điểm J, L, M, G, E, C, I.
Từ đó suy ra phép đối xứng tâm O biến các tam giác IKN, KHF, HJD tương ứng thành các tam giác JLM, LGE, GIC hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Ta có và OK = OJ nên ta có phép quay tâm O với góc quay – 120° biến điểm K thành điểm J.
Ta có và OH = OL nên ta có phép quay tâm O với góc quay – 120° biến điểm H thành điểm L.
Ta có và OF = OM nên ta có phép quay tâm O với góc quay – 120° biến điểm F thành điểm M.
Do đó, ta có phép quay tâm O với góc quay – 120° biến tam giác KHF thành tam giác JLM.
Tương tự, ta có phép quay tâm O với góc quay – 120° biến tam giác LGE thành tam giác IKN.
Như vậy, phép quay tâm O với góc quay – 120° biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.
Câu 39:
23/07/2024Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Xác định một phép dời hình biến:
a) Tam giác AMQ thành tam giác CPN;
b) Tam giác AMO thành tam giác PCN.
 Xem đáp án
Xem đáp án
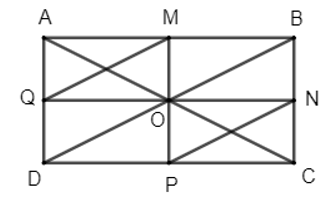
a) Vì O là giao hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có M và O lần lượt là trung điểm của AB và AC nên MO là đường trung bình của tam giác ABC, suy ra MO // BC và MO = BC (1).
Xét tam giác DBC có O và P lần lượt là trung điểm của BD và DC nên OP là đường trung bình của tam giác DBC, suy ra OP // BC và OP = BC (2).
Từ (1) và (2) suy ra O, P, M thẳng hàng và OM = OP nên O là trung điểm của PM.
Chứng minh tương tự ta được O là trung điểm của QN.
Do đó, ta có phép đối xứng tâm O biến các điểm A, M, Q tương ứng thành các điểm C, P, N.
Như vậy, phép đối xứng tâm O biến tam giác AMQ thành tam giác CPN.
b) Ta có QN // AB // CD và AD ⊥ AB nên AD ⊥ QN, mà Q là trung điểm của AD nên QN là đường trung trực của đoạn thẳng AD.
Ta có AD // MP nên QN ⊥ MP, mà O là trung điểm của MP nên QN là đường trung trực của đoạn thẳng MP.
Do đó, ta có phép đối xứng trục QN biến các điểm A, M, O tương ứng thành các điểm D, P, O.
Như vậy, phép đối xứng trục QN biến tam giác AMO thành tam giác DPO (3).
Ta lại có: , do đó ta có phép tịnh tiến theo vectơ biến các điểm D, P, O tương ứng thành các điểm P, C, N. Khi đó, phép tịnh tiến theo vectơ biến tam giác DPO thành tam giác PCN (4).
Từ (3) và (4) ta suy ra phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng trục QN và phép tịnh tiến theo vectơ (ĐQN trước, sau) biến tam giác AMO thành tam giác PCN.
Câu 40:
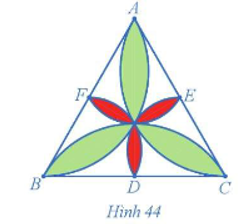
12/07/2024Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
a) Cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.
 Xem đáp án
Xem đáp án
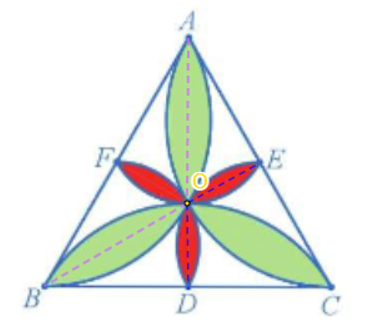
a) Đặt điểm O là tâm của các cánh hoa như hình vẽ. Do tam giác ABC là tam giác đều nên OA = OB và . Do đó, ta có phép quay tâm O với góc quay 120° biến điểm O thành điểm O và điểm A thành điểm B. Như vậy, phép quay tâm O với góc quay 120° biến cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Ta cũng có OE = OD và A nên ta có phép quay tâm O với góc quay – 120° biến điểm O thành điểm O, biến điểm E thành điểm D. Như vậy, phép quay tâm O với góc quay – 120° biến cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.
Câu 41:
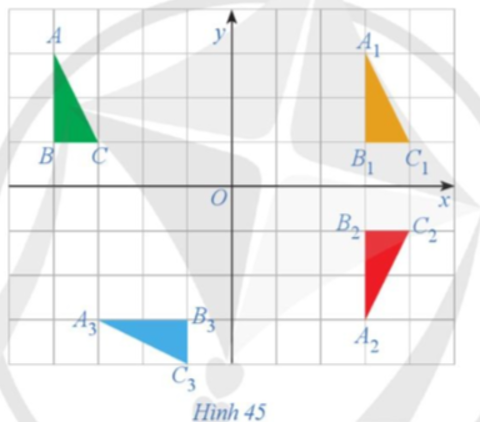
21/07/2024Quan sát Hình 45. Xác định các phép dời hình biến tam giác ABC thành tam giác A1B1C1, tam giác A1B1C1 thành tam giác A2B2C2, tam giác A2B2C2 thành tam giác A3B3C3.
 Xem đáp án
Xem đáp án
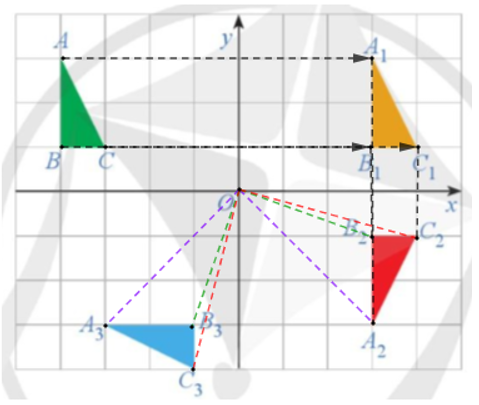
+) Ta có: nên ta có phép tịnh tiến theo vectơ biến các điểm A, B, C tương ứng thành các điểm A1, B1, C1. Do đó, phép tịnh tiến theo vectơ biến tam giác ABC thành tam giác A1B1C1.
+) Ox là đường trung trực của các đoạn thẳng A1A2, B1B2 và C1C2 nên ta có phép đối xứng trục Ox biến các điểm A1, B1, C1 tương ứng thành các điểm A2, B2, C2. Do đó, phép đối xứng trục Ox biến tam giác A1B1C1 thành tam giác A2B2C2.
+) Ta có: OA2 = OA3, OB2 = OB3, OC2 = OC3 (đường chéo của các hình chữ nhật có cùng kích thước) và , phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ, do đó phép quay tâm O với góc quay – 90° biến các điểm A2, B2, C2 tương ứng thành các điểm A3, B3, C3. Vậy ta có phép quay tâm O với góc quay – 90° biến tam giác A2B2C2 thành tam giác A3B3C3.
Câu 43:
20/07/2024Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.
a) Xác định điểm C đối xứng với B qua trục hoành.
b) Chứng minh rằng MB = MC.
c) Xác định điểm M sao cho tổng MA + MB đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
a) Điểm B(6; 3) đối xứng với điểm C qua trục hoành Ox nên C là ảnh của B qua phép đối xứng trục Ox. Do đó C(6; – 3).
b) Vì C là ảnh của điểm B qua phép đối xứng trục Ox nên Ox là đường trung trực của đoạn thẳng BC, do đó điểm M thuộc đường trung trực Ox của BC thì M cách đều B và C, suy ra MB = MC.
c)
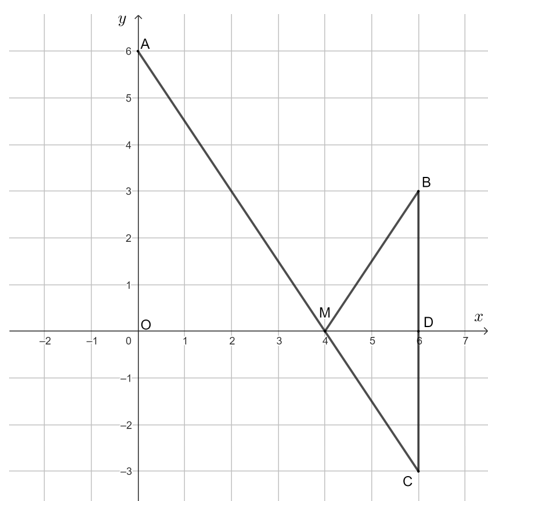
Vì MB = MC nên MA + MB = MA + MC.
Do A và C nằm khác phía nhau đối với trục Ox và M thuộc Ox nên MA + MC ≥ AC.
Dấu “=” xảy ra khi M thuộc AC.
Như vậy M là giao điểm của AC và Ox thì tổng MA + MB đạt giá trị nhỏ nhất bằng AC.
Ta có: , .
Gọi D là giao điểm của BC và Ox, khi đó CD = BC = 3 và OA // CD.
Suy ra . Suy ra OM = 2MD nên OM = OD = .6 = 4.
Do đó, M(4; 0).
Vậy M(4; 0) thì tổng MA + MB đạt giá trị nhỏ nhất.
Câu 44:
20/07/2024Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.
 Xem đáp án
Xem đáp án
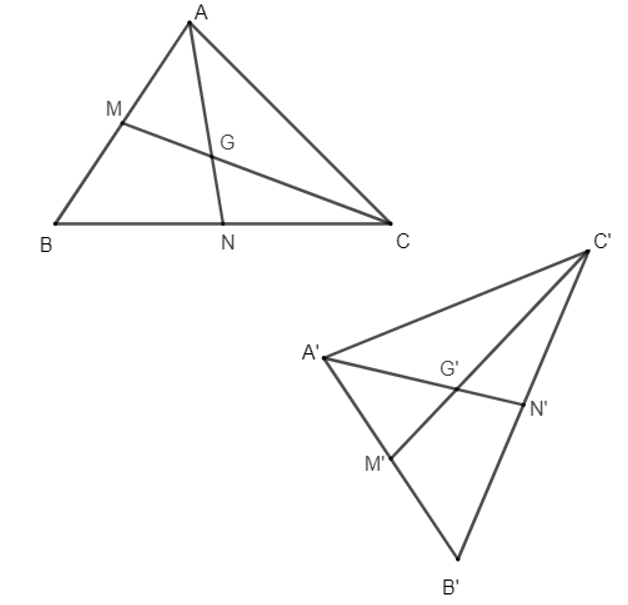
+) Phép dời hình F biến tam giác ABC thành tam giác A'B'C', do đó F biến các đoạn thẳng AB, BC tương ứng thành các đoạn thẳng A'B', B'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, BC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', B'C'. Vậy F biến các trung tuyến CM, AN của tam giác ABC tương ứng thành các trung tuyến C'M', A'N' của tam giác A'B'C'. Từ đó suy ra F biến trọng tâm G của tam giác ABC là giao của CM và AN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và A'N'.
+) Gọi AH là đường cao của tam giác ABC (H ∈ BC). Khi đó phép dời hình F biến đường thẳng AH thành đường thẳng A'H'. Vì AH ⊥ BC nên A'H' ⊥ B'C', nói cách khác A'H' là đường cao của tam giác A'B'C'. Đối với các đường cao khác cũng thế. Vì trực tâm tam giác là giao điểm của các đường cao nên trực tâm tam giác ABC biến thành trực tâm tam giác A'B'C'.
+) Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC thì OA = OB = OC nên nếu điểm O biến thành điểm O' qua phép dời hình F thì O'A' = O'B' = O'C' = OA = OB = OC, do đó O' là tâm đường tròn ngoại tiếp tam giác A'B'C'.