Cho hàm số f(x) liên tục trên Rvà thỏa mãn ${\int }_{-5}^{1}f\left(x\right)dx = 9$ Tính ${\int }_0^2\left[f(1-3x)+9\right]dx$

Đáp án đúng là B

Lời giải

*Phương pháp giải:

Định lí: Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [a; b] thì

$\underset{a}{\overset{b}{\int }}u\left(x\right)v\text{'}\left(x\right)dx={\left.\left[u\left(x\right)v\left(x\right)\right]\right|}_a^b-\underset{a}{\overset{b}{\int }}u\text{'}\left(x\right)v\left(x\right)dx$, hay viết gọn là $\underset{a}{\overset{b}{\int }}udv=uv{|}_a^b-\underset{a}{\overset{b}{\int }}vdu$

*Lý thuyết:

1. Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

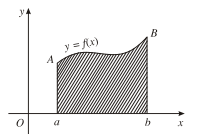
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a; x = b (a < b); trục hoành và đường cong y = f(x), trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in \left[a;b\right]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

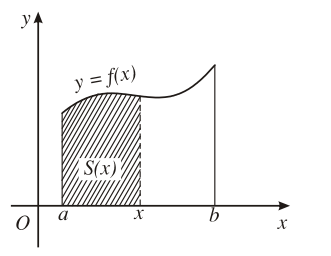
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) + C.

Vì S(a) = 0 nên F(a) + C = 0 hay C = – F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

2. Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$

Ta còn dùng kí hiệu ${\left.F\left(x\right)\right|}_a^b$ để chỉ hiệu số F(b) – F(a).

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=$${\left.F\left(x\right)\right|}_a^b=F\left(b\right)-F\left(a\right)$

Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

- Chú ý.

Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;$$\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)\text{}dx$

Xem thêm

Lý thuyết Tích phân (mới 2024 + Bài Tập) – Toán 12 

TOP 40 câu Trắc nghiệm Ứng dụng tích phân (có đáp án 2024) - Toán 12