Câu hỏi:
18/07/2024 186
Cho f(x) = 2x4 – 4x2 + 6x3 + 2x + 3; g(x) = x + 3 và f(x) + k(x) = g(x). Hệ số tự do của đa thức k(x) là:
Cho f(x) = 2x4 – 4x2 + 6x3 + 2x + 3; g(x) = x + 3 và f(x) + k(x) = g(x). Hệ số tự do của đa thức k(x) là:
A. -1
B. 4
C. 0
D. 6
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Ta có f(x) + k(x) = g(x)
Suy ra k(x) = g(x) – f(x)
= x + 3 – (2x4 – 4x2 + 6x3 + 2x + 3)
= x + 3 – 2x4 + 4x2 – 6x3 – 2x – 3
= –2x4 – 6x3 + 4x2 + (x – 2x) + 3 – 3
= –2x4 – 6x3 + 4x2 – x
Vậy hệ số tự do của k(x) là 0.
Đáp án đúng là: C
Ta có f(x) + k(x) = g(x)
Suy ra k(x) = g(x) – f(x)
= x + 3 – (2x4 – 4x2 + 6x3 + 2x + 3)
= x + 3 – 2x4 + 4x2 – 6x3 – 2x – 3
= –2x4 – 6x3 + 4x2 + (x – 2x) + 3 – 3
= –2x4 – 6x3 + 4x2 – x
Vậy hệ số tự do của k(x) là 0.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác như hình vẽ dưới đây, có chu vi bằng 6x – 10.
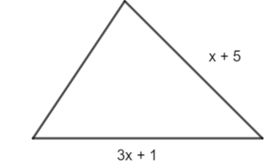
Độ dài cạnh chưa biết của tam giác trên là:
Cho tam giác như hình vẽ dưới đây, có chu vi bằng 6x – 10.
Độ dài cạnh chưa biết của tam giác trên là:
Câu 3:
Bạn Minh nói: Tổng của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Quân nói: Hiệu của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Nam nói: Tổng của hai đa thức bậc ba chưa chắc là đa thức bậc ba.
Chọn khẳng định đúng.
Bạn Minh nói: Tổng của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Quân nói: Hiệu của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Nam nói: Tổng của hai đa thức bậc ba chưa chắc là đa thức bậc ba.
Chọn khẳng định đúng.
Câu 4:
Cho P(x) = 3x4 + 4x3 – 3x2 + 2x – 1 và Q(x) = –x4 + 2x3 – 3x2 + 4x – 5.
Tính P(x) + Q(x) rồi tìm bậc của đa thức thu gọn.
Cho P(x) = 3x4 + 4x3 – 3x2 + 2x – 1 và Q(x) = –x4 + 2x3 – 3x2 + 4x – 5.
Tính P(x) + Q(x) rồi tìm bậc của đa thức thu gọn.
Câu 5:
Cho đa thức P(x) = –6x5 – 4x4 + 3x2 – 2x và Q(x) = 2x5 – 4x4 – 2x3 + 2x2 – x – 3. Tính M(1) với M(x) = P(x) – Q(x).
Câu 6:
A(x) = 5x4 + 4x3 + 2x + 1 và B(x) = –5x4 + x3 + 3x2 + x – 1. Bậc của đa thức N(x) = A(x) + B(x) là:
A(x) = 5x4 + 4x3 + 2x + 1 và B(x) = –5x4 + x3 + 3x2 + x – 1. Bậc của đa thức N(x) = A(x) + B(x) là:
Câu 7:
Người ta rót nước từ một can đựng 20 lít nước sang một bể rỗng có dạng hình lập phương với cạnh 40 cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1 dm3.
Người ta rót nước từ một can đựng 20 lít nước sang một bể rỗng có dạng hình lập phương với cạnh 40 cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1 dm3.
Câu 8:
Cho f(x) = 3x5 – 3x4 + x2 – 5 và g(x) = 2x4 – x3 – x2 + 5.
Tính hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
Cho f(x) = 3x5 – 3x4 + x2 – 5 và g(x) = 2x4 – x3 – x2 + 5.
Tính hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
Câu 9:
Cho hai đa thức f(x) = 6x2 + 4x – 5 và g(x) = –6x2 – 4x + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x).
Cho hai đa thức f(x) = 6x2 + 4x – 5 và g(x) = –6x2 – 4x + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x).
Câu 10:
Một mảnh đất hình chữ nhật có kích thước chiều dài, chiều rộng lần lượt là 3x m và 2 m. Người ta dự định trồng hoa trong phần đất hình vuông có cạnh là x m như hình vẽ.
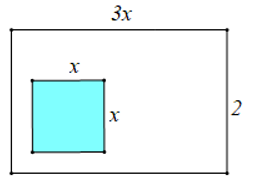
Diện tích phần đất còn lại (phần đất không tô màu) là:
Một mảnh đất hình chữ nhật có kích thước chiều dài, chiều rộng lần lượt là 3x m và 2 m. Người ta dự định trồng hoa trong phần đất hình vuông có cạnh là x m như hình vẽ.
Diện tích phần đất còn lại (phần đất không tô màu) là:
Câu 11:
Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = 5x4 – 4x2 + 6x3 + x – 1; g(x) = 3 – 2x.
Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = 5x4 – 4x2 + 6x3 + x – 1; g(x) = 3 – 2x.
Câu 12:
Xác định P(x) = ax2 + bx + c biết P(1) = 0; P(–1) = 6 và P(2) = 3
Câu 13:
Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) – Q(x) = 2x – 2 là:
Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) – Q(x) = 2x – 2 là:
Câu 14:
Cho hai đa thức f(x) = x2 + 3x – 5 và g(x) = –5x2 – x + 2.
Tính k(x) = f(x) –g(x) và tìm bậc của k(x).
Cho hai đa thức f(x) = x2 + 3x – 5 và g(x) = –5x2 – x + 2.
Tính k(x) = f(x) –g(x) và tìm bậc của k(x).


