Câu hỏi:
06/07/2024 111
Bề mặt trên của mỗi bậc thang này được đặt như thế nào so với mặt đất?

Bề mặt trên của mỗi bậc thang này được đặt như thế nào so với mặt đất?

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Bề mặt trên của mỗi bậc thang được đặt song song với mặt đất.
Bề mặt trên của mỗi bậc thang được đặt song song với mặt đất.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M’, N’.
a) Chứng minh (CBE) // (ADF).
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M’, N’.
a) Chứng minh (CBE) // (ADF).
Câu 2:
Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượT đi qua các điểm A, B, C, D. Một mặt phẳng (Q) cắt bốn nửa đường thẳng nói trên tại A’, B’, C’, D’. Chứng minh rằng:
AA’ + CC’ = BB’ + DD’.
Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượT đi qua các điểm A, B, C, D. Một mặt phẳng (Q) cắt bốn nửa đường thẳng nói trên tại A’, B’, C’, D’. Chứng minh rằng:
AA’ + CC’ = BB’ + DD’.
Câu 3:
b) Gọi E là trung điểm của AB và F là một điểm thuộc ON. Chứng minh EF song song với (SBC).
b) Gọi E là trung điểm của AB và F là một điểm thuộc ON. Chứng minh EF song song với (SBC).
Câu 4:
Cho hình hộp ABCD.A’B’C’D’. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác BDA’ và B’D’C. Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
Cho hình hộp ABCD.A’B’C’D’. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác BDA’ và B’D’C. Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
Câu 5:
Cho tứ diện ABCD có E, F, H lần lượt là trung điểm của AB, AC, AD. Chứng minh (EFH) // (BCD).
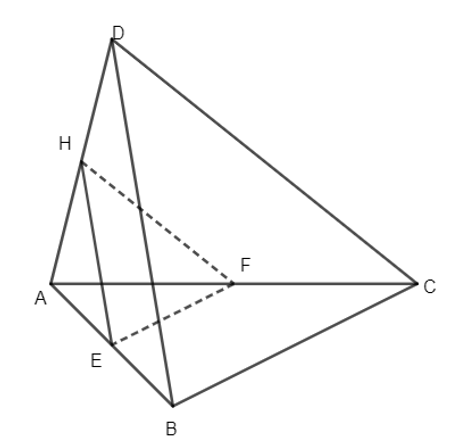
Cho tứ diện ABCD có E, F, H lần lượt là trung điểm của AB, AC, AD. Chứng minh (EFH) // (BCD).

Câu 6:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của SA, SD.
a) Chứng minh rằng (OMN) // (SBC).
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của SA, SD.
a) Chứng minh rằng (OMN) // (SBC).
Câu 7:
Cho hình hộp ABCD.A’B’C’D’và một mặt phẳng (α) cắt các mặt của hình hộp theo các giao tuyến MN, NP, PQ, QR, RS, SM như Hình 18. Chứng minh các cặp cạnh đối của lục giác MNPQRS song song với nhau.
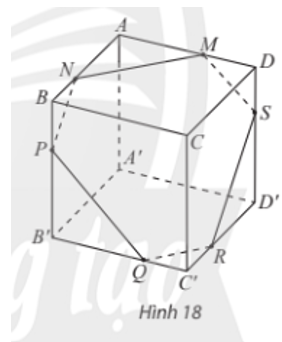
Cho hình hộp ABCD.A’B’C’D’và một mặt phẳng (α) cắt các mặt của hình hộp theo các giao tuyến MN, NP, PQ, QR, RS, SM như Hình 18. Chứng minh các cặp cạnh đối của lục giác MNPQRS song song với nhau.

Câu 8:
Cho mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q). Giả sử (P) và (Q) có điểm chung M thì (P) cắt (Q) theo giao tuyến c (Hình 5).

a) Gải thích tại sao đường thẳng c phải cắt ít nhất một trong hai đường thẳng a, b. Điều này có trái với giả thiết a và b cùng song song với (Q) không?
b) Rút ra kết luận về số điểm chung và vị trí tương đối của (P) và (Q).
Cho mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q). Giả sử (P) và (Q) có điểm chung M thì (P) cắt (Q) theo giao tuyến c (Hình 5).

a) Gải thích tại sao đường thẳng c phải cắt ít nhất một trong hai đường thẳng a, b. Điều này có trái với giả thiết a và b cùng song song với (Q) không?
b) Rút ra kết luận về số điểm chung và vị trí tương đối của (P) và (Q).
Câu 9:
Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về mặt phẳng song song trong thực tế.

Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về mặt phẳng song song trong thực tế.

Câu 10:
Hộp giấy có các mặt là hình vuông ở Hình 1a được vé lại với các đỉnh là A, B, C, D, A’, B’, C’, D’ như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.
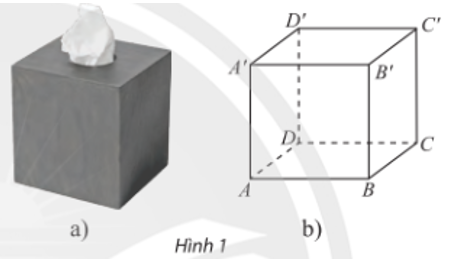
Hộp giấy có các mặt là hình vuông ở Hình 1a được vé lại với các đỉnh là A, B, C, D, A’, B’, C’, D’ như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.

Câu 11:
Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo, tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và cắt đoạn thằng AC. Chứng minh các giao tuyến của (α) với hình chóp tạo thành một tam giác đều.
Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo, tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và cắt đoạn thằng AC. Chứng minh các giao tuyến của (α) với hình chóp tạo thành một tam giác đều.
Câu 12:
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A’B’C’D’E’F’, Bình gắn hai thanh tre A1D1, F1C1 song song với mặt phẳng đáy và cắt nhau tại O1 (Hình 19).
a) Xác định giao tuyến của mp(A1D1, F1C1) với các mặt bên của lăng trụ.
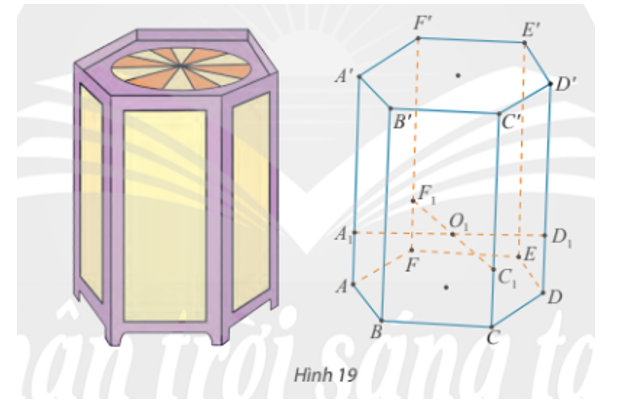
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A’B’C’D’E’F’, Bình gắn hai thanh tre A1D1, F1C1 song song với mặt phẳng đáy và cắt nhau tại O1 (Hình 19).
a) Xác định giao tuyến của mp(A1D1, F1C1) với các mặt bên của lăng trụ.

Câu 14:
Cho hình chóp S.ABC có SA = 9, SB = 12, SC = 15. Trên cạnh SA lấy điểm M, N sao cho SM = 4, MN = 3, NA = 2. Vẽ hai mặt phẳng song song với mặt phẳng (ABC), lần lượt đi qua M, N, cắt SB theo thứ tự tại M’, N’ và cắt SC theo thứ tự tại M”, N”. Tính độ dài các đoạn thẳng SM’, M’N’, M”N”, N”C.
Cho hình chóp S.ABC có SA = 9, SB = 12, SC = 15. Trên cạnh SA lấy điểm M, N sao cho SM = 4, MN = 3, NA = 2. Vẽ hai mặt phẳng song song với mặt phẳng (ABC), lần lượt đi qua M, N, cắt SB theo thứ tự tại M’, N’ và cắt SC theo thứ tự tại M”, N”. Tính độ dài các đoạn thẳng SM’, M’N’, M”N”, N”C.


