Câu hỏi:
22/07/2024 168
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b) Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy như sau:
Nhóm
Giá trị đại diện
Tần số
Tần số tích lũy
[40; 45)
42,5
4
4
[45; 50)
47,5
11
15
[50; 55)
52,5
7
22
[55; 60)
57,5
8
30
[60; 65)
62,5
8
38
[65; 70)
67,5
2
40
n = 40
⦁ Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:
⦁ Số phần tử của mẫu là n = 40. Ta có
Mà 15 < 20 < 22 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [50; 55) có r = 50, d = 5, n3 = 7 và nhóm 2 là nhóm [45; 50) có cf2 = 15.
Áp dụng công thức, ta có trung vị của mẫu số liệu là:
(km/h).
Do đó tứ phân vị thứ hai là Q2 = Me ≈ 53,6 (km/h).
⦁ Ta có . Mà 4 < 10 < 15 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [45; 50) có s = 45; h = 5; n2 = 11 và nhóm 1 là nhóm [40; 45) có cf1 = 4.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(km/h).
⦁ Ta có . Mà cf4 = 30 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm [55; 60) có t = 55; l = 5; n4 = 8 và nhóm 3 là nhóm [50; 55) có cf1 = 22.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(km/h).
b) Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy như sau:
|
Nhóm |
Giá trị đại diện |
Tần số |
Tần số tích lũy |
|
[40; 45) |
42,5 |
4 |
4 |
|
[45; 50) |
47,5 |
11 |
15 |
|
[50; 55) |
52,5 |
7 |
22 |
|
[55; 60) |
57,5 |
8 |
30 |
|
[60; 65) |
62,5 |
8 |
38 |
|
[65; 70) |
67,5 |
2 |
40 |
|
|
|
n = 40 |
|
⦁ Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:
⦁ Số phần tử của mẫu là n = 40. Ta có
Mà 15 < 20 < 22 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [50; 55) có r = 50, d = 5, n3 = 7 và nhóm 2 là nhóm [45; 50) có cf2 = 15.
Áp dụng công thức, ta có trung vị của mẫu số liệu là:
(km/h).
Do đó tứ phân vị thứ hai là Q2 = Me ≈ 53,6 (km/h).
⦁ Ta có . Mà 4 < 10 < 15 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [45; 50) có s = 45; h = 5; n2 = 11 và nhóm 1 là nhóm [40; 45) có cf1 = 4.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(km/h).
⦁ Ta có . Mà cf4 = 30 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm [55; 60) có t = 55; l = 5; n4 = 8 và nhóm 3 là nhóm [50; 55) có cf1 = 22.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(km/h).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một trường trung học phổ thông chọn 36 học sinh nam của khối 11, đo chiều cao của các bạn học sinh đó và thu được mẫu số liệu sau (đơn vị: centimét):
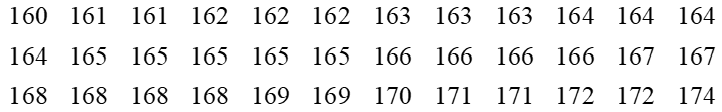
Từ mẫu số liệu không ghép nhóm trên, hãy ghép các số liệu thành năm nhóm theo các nửa khoảng có độ dài bằng nhau.
Câu 2:
Mẫu số liệu sau ghi lại cân nặng của 30 bạn học sinh (đơn vị: kilôgam):
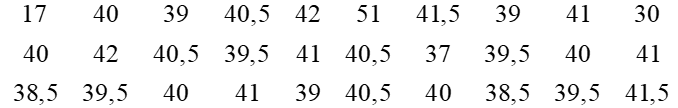
a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
[15; 20), [20; 25), [25; 30), [30; 35), [35; 40), [40; 45), [45; 50), [50; 55).
Mẫu số liệu sau ghi lại cân nặng của 30 bạn học sinh (đơn vị: kilôgam):
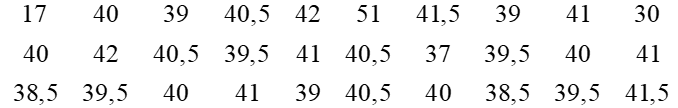
a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
[15; 20), [20; 25), [25; 30), [30; 35), [35; 40), [40; 45), [45; 50), [50; 55).
Câu 3:
Một cuộc khảo sát đã tiến hành xác định tuổi (theo năm) của 120 chiếc ô tô. Kết quả điều tra được cho trong Bảng 1.

Tìm các số đặc trưng đo xu thế trung tâm (số trung bình cộng, trung vị, tứ phân vị, mốt) cho mẫu số liệu ghép nhóm đó như thế nào cho thuận lợi?
Một cuộc khảo sát đã tiến hành xác định tuổi (theo năm) của 120 chiếc ô tô. Kết quả điều tra được cho trong Bảng 1.

Tìm các số đặc trưng đo xu thế trung tâm (số trung bình cộng, trung vị, tứ phân vị, mốt) cho mẫu số liệu ghép nhóm đó như thế nào cho thuận lợi?
Câu 4:
Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm (đơn vị: phút) và lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy như Bảng 12.
Nhóm
Tần số
Tần số tích lũy
[0; 60)
[60; 120)
[120; 180)
[180; 240)
[240; 300)
6
13
13
6
2
6
19
32
38
40
n = 40
Bảng 12
a) Tìm trung vị Me của mẫu số liệu ghép nhóm đó. Trung vị Me còn gọi là tứ phân vị thứ hai Q2 của mẫu số liệu trên.
Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm (đơn vị: phút) và lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy như Bảng 12.
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[0; 60) [60; 120) [120; 180) [180; 240) [240; 300) |
6 13 13 6 2 |
6 19 32 38 40 |
|
|
n = 40 |
|
Bảng 12
a) Tìm trung vị Me của mẫu số liệu ghép nhóm đó. Trung vị Me còn gọi là tứ phân vị thứ hai Q2 của mẫu số liệu trên.
Câu 5:
Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích luỹ ở Ví dụ 6 rồi cho biết:
Nhóm
Tần số
Tần số tích lũy
[30; 40)
[40; 50)
[50; 60)
[60; 70)
[70; 80)
[80; 90)
2
10
16
8
2
2
1
12
28
36
38
40
n = 40
Bảng 13
a) Nhóm nào có tần số lớn nhất;
b) Đầu mút trái và độ dài của nhóm có tần số lớn nhất bằng bao nhiêu.
Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích luỹ ở Ví dụ 6 rồi cho biết:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[30; 40) [40; 50) [50; 60) [60; 70) [70; 80) [80; 90) |
2 10 16 8 2 2 |
1 12 28 36 38 40 |
|
|
n = 40 |
|
Bảng 13
a) Nhóm nào có tần số lớn nhất;
b) Đầu mút trái và độ dài của nhóm có tần số lớn nhất bằng bao nhiêu.
Câu 6:
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h).
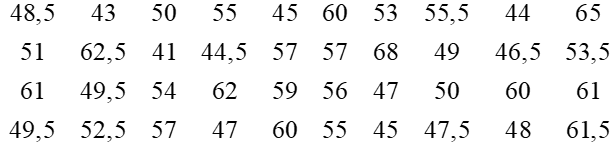
a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
[40; 45), [45; 50), [50; 55), [55; 60), [60; 65), [65; 70).
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h).

a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
[40; 45), [45; 50), [50; 55), [55; 60), [60; 65), [65; 70).
Câu 7:
Bảng 15 cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao của 40 mẫu cây ở một vườn thực vật (đơn vị: centimét).
Nhóm
Tần số
Tần số tích lũy
[30; 40)
[40; 50)
[50; 60)
[60; 70)
[70; 80)
[80; 90)
4
10
14
6
4
2
4
14
28
34
38
40
n = 40
Bảng 15
a) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
Bảng 15 cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao của 40 mẫu cây ở một vườn thực vật (đơn vị: centimét).
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[30; 40) [40; 50) [50; 60) [60; 70) [70; 80) [80; 90) |
4 10 14 6 4 2 |
4 14 28 34 38 40 |
|
|
n = 40 |
|
Bảng 15
a) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
Câu 8:
Trong phòng thí nghiệm, người ta chia 99 mẫu vật thành năm nhóm căn cứ trên khối lượng của chúng (đơn vị: gam) và lập bảng tần số ghép nhóm bao gồm cả tần số tích luỹ như Bảng 10.
Nhóm
Tần số
Tần số tích lũy
[27,5; 32,5)
[32,5; 37,5)
[37,5; 42,5)
[42,5; 47,5)
[47,5; 52,5)
16
24
20
30
9
16
40
60
90
99
n = 99
Bảng 10
a) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng có đúng không?
b) Tìm đầu mút trái r, độ dài d, tần số n3 của nhóm 3; tần số tích lũy cf2 của nhóm 2.
c) Tính giá trị Me theo công thức sau:
Giá trị Me được gọi là trung vị của mẫu số liệu ghép nhóm đã cho.
Trong phòng thí nghiệm, người ta chia 99 mẫu vật thành năm nhóm căn cứ trên khối lượng của chúng (đơn vị: gam) và lập bảng tần số ghép nhóm bao gồm cả tần số tích luỹ như Bảng 10.
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[27,5; 32,5) [32,5; 37,5) [37,5; 42,5) [42,5; 47,5) [47,5; 52,5) |
16 24 20 30 9 |
16 40 60 90 99 |
|
|
n = 99 |
|
Bảng 10
a) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng có đúng không?
b) Tìm đầu mút trái r, độ dài d, tần số n3 của nhóm 3; tần số tích lũy cf2 của nhóm 2.
c) Tính giá trị Me theo công thức sau:
Giá trị Me được gọi là trung vị của mẫu số liệu ghép nhóm đã cho.
Câu 9:
Một thư viện thống kê người đến đọc sách vào buổi tối trong 30 ngày của tháng vừa qua như sau:

Lập bảng tần số ghép nhóm có tám nhóm ứng với tám nửa khoảng sau:
[25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79); [79; 88); [88; 97).
Một thư viện thống kê người đến đọc sách vào buổi tối trong 30 ngày của tháng vừa qua như sau:

Lập bảng tần số ghép nhóm có tám nhóm ứng với tám nửa khoảng sau:
[25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79); [79; 88); [88; 97).
Câu 10:
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 4).
Nhóm
Tần số
[160; 163)
[163; 166)
[166; 169)
[169; 172)
[172; 175)
6
12
10
5
3
n = 36
Bảng 4
a) Tìm trung điểm x1 của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm 1. Ta gọi trung điểm x1 là giá trị đại diện của nhóm 1.
b) Bằng cách tương tự, hãy tìm giá trị đại diện của bốn nhóm còn lại. Từ đó, hãy hoàn thiện các số liệu trong Bảng 7.
Nhóm
Giá trị đại diện
Tần số
[160; 163)
[163; 166)
[166; 169)
[169; 172)
[172; 175)
x1 = ?
x2 = ?
x3 = ?
x4 = ?
x5 = ?
n1 = ?
n2 = ?
n3 = ?
n4 = ?
n5 = ?
n = ?
Bảng 7
c) Tính giá trị cho bởi công thức sau:
Giá trị gọi là số trung bình cộng của mẫu số liệu đã cho.
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 4).
|
Nhóm |
Tần số |
|
[160; 163) [163; 166) [166; 169) [169; 172) [172; 175) |
6 12 10 3 |
|
|
n = 36 |
Bảng 4
a) Tìm trung điểm x1 của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm 1. Ta gọi trung điểm x1 là giá trị đại diện của nhóm 1.
b) Bằng cách tương tự, hãy tìm giá trị đại diện của bốn nhóm còn lại. Từ đó, hãy hoàn thiện các số liệu trong Bảng 7.
|
Nhóm |
Giá trị đại diện |
Tần số |
|
[160; 163) [163; 166) [166; 169) [169; 172) [172; 175) |
x1 = ? x2 = ? x3 = ? x4 = ? x5 = ? |
n1 = ? n2 = ? n3 = ? n4 = ? n5 = ? |
|
|
|
n = ? |
Bảng 7
c) Tính giá trị cho bởi công thức sau:
Giá trị gọi là số trung bình cộng của mẫu số liệu đã cho.
Câu 12:
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
Câu 14:
Trong bài toán ở Luyện tập 2, lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có tám nhóm ứng với tám nửa khoảng:
[25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79); [79; 88); [88; 97).
Trong bài toán ở Luyện tập 2, lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có tám nhóm ứng với tám nửa khoảng:
[25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79); [79; 88); [88; 97).
Câu 15:
Xác định trung vị của mẫu số liệu ghép nhóm ở Bảng 1.
Nhóm
Tần số
[0; 4)
13
[4; 8)
29
[8; 12)
48
[12; 16)
22
[16; 20)
8
n = 120
Bảng 1
Xác định trung vị của mẫu số liệu ghép nhóm ở Bảng 1.
|
Nhóm |
Tần số |
|
[0; 4) |
13 |
|
[4; 8) |
29 |
|
[8; 12) |
48 |
|
[12; 16) |
22 |
|
[16; 20) |
8 |
|
|
n = 120 |
Bảng 1


