Đề thi vào 10 môn Toán TP Hồ Chí Minh chính thức (2022) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi vào 10 môn Toán TP Hồ Chí Minh chính thức (các năm) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hồ Chí Minh có đáp án - năm 2022

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TP HCM - 2022-2023

Bài 1:

Bài 2:

Bài 3:

Bài 4:

Bài 5:

Bài 6:

Bài 7:

Bài 8:

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2020 - 2021

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hồ Chí Minh có đáp án - năm 2020

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2019 - 2020

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Thành phố Hồ Chí Minh có đáp án (Tự luận) - năm 2019

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2016 - 2017

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Thành phố Hồ Chí Minh có đáp án (Tự luận) - năm 2016

Bài 1. (2 điểm)

Giải các phương trình và hệ phương trình sau

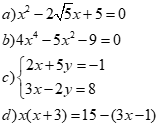
Bài 2. (1,5 điểm)

a) Vẽ đồ thị (P) của hàm số $y=\frac{-x^2}{4}$ và đường thẳng (D): $y=\frac{x}{2}-2$ trên cùng một hệ trục tọa độ

b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính

Bài 3. (1,5 điểm)

a) Thu gọn biểu thức $A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}$

b) Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kỳ hạn 1 năm là 6%. Tuy nhiên sau thời hạn một năm ông Sáu không đến nhận tiền lãi mà để thêm một năm nữa mới lãnh. Khi đó số tiền lãi có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi cho năm kế tiếp với mức lãi suất cũ. Sau 2 năm ông Sáu nhận được số tiền là 112.360.000 đồng (kể cả gốc lẫn lãi). Hỏi ban đầu ông Sáu đã gửi bao nhiêu tiền?

Bài 4. (1,5 điểm)

Cho phương trình: $x^2-2mx+m-2=0$ (1) (x là ẩn số)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m

b) Định m để hai nghiệm x₁, x₂ của phương trình (1) thỏa mãn $(1+x_1)(2-x_2)+(1+x_2)(2-x_1)={x_1}^2+{x_2}^2+2$

Bài 5. (3,5 điểm)

Cho ∆ ABC (AB < AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE; F là giao điểm của AH và BC.

a) Chứng minh AF ⊥ BC và góc AFD = góc ACE

b) Gọi M là trung điểm của AH. Chứng minh MD ⊥ OD và 5 điểm M, D, O, F, E cùng thuộc một đường tròn.

c) Gọi K là giao điểm của AH và DE. Chứng minh MD² = MK.MF và K là trực tâm của ∆ MBC

d) Chứng minh $\frac{2}{FK}=\frac{1}{FH}+\frac{1}{FA}$

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TPHCM NĂM 2016 – 2017

Bài 1.(2,0 điểm)

Giải các phương trình và hệ phương trình:

$$\begin{gathered} a) x^2-2\sqrt{5}+5=0 \\ \iff {(x-\sqrt{5})}^2=0\iff x-\sqrt{5}=0 \\ \iff x=\sqrt{5} \end{gathered}$$

Vậy phương trình đã cho có tập nghiệm S = {$\sqrt{5}$}

$b) 4x^2-5x^2-9=0$

Đặt x² = t (t ≥ 0)

Khi đó phương trình trở thành: $4t^2-5t-9=0$ (*)

Ta có: a - b + c = 4 - (-5) - 9 = 0

Nên ta có phương trình (*) có 2 nghiệm phân biệt là: t = - 1 (loại) và $t=\frac{9}{4}$ (thỏa mãn điều kiện)

Với $t=\frac{9}{4}$ ta có: $x^2=\frac{9}{4}\iff x=\pm \frac{3}{2}$

Vậy phương trình đã cho có tập nghiêm là: $S=\left\{\frac{-3}{2};\frac{3}{2}\right\}$

c.

$$\begin{gathered} \left\{\begin{array}{l}2x+5y=-1\\ 3x-2y=8\end{array}\iff \left\{\begin{array}{l}6x+12y=-3\\ 6x-4y=16\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}19y=-19\\ 3x-2y=8\end{array}\iff \left\{\begin{array}{l}x=2\\ y=-1\end{array}\right.\right. \end{gathered}$$

Vậy hệ phương trình có 1 nghiệm duy nhất (x;y) = (2;-1).

d)

 $$\begin{gathered} x(x-3)=15-(3x-1) \\ \iff x^2+6x-16=0 \\ ∆\text{'}=9+16=25>0 \end{gathered}$$

Khi đó phương trình có 2 nghiệm phân biệt là: x = - 8; x = 2

Vậy tập nghiệm của phương trình đã cho là S = {-8;2}

Bài 2.(1,5 điểm).

a)Vẽ đồ thị hai hàm số.

Bảng giá trị

Đồ thị

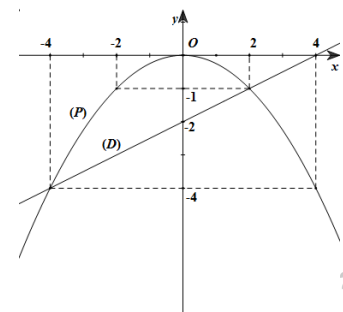
b)Tìm tọa độ giao điểm của (d) và (P) bằng phép tính

Xét phương trình hoành độ giao điểm của (d) và (P)

$$\begin{gathered} \frac{-x^2}{4}=\frac{x}{2}-2 \iff x^2+2x-8=0 \\ ∆\text{'}=9 \end{gathered}$$

Phương trình trên có hai nghiệm phân biệt: x₁=2; x₂=-4

Với x₁=2 ta có y₁=-1, A(2;-1)

Với x₁=2 ta có y₁=-1, A(2;-1)

Vậy (d) cắt (P) tại hai điểm phân biệt A(2 ;-1) ; B(-4 ;-4)

Bài 3 (1,5 điểm)

a.

$$\begin{gathered} A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}} \\ = \frac{2-\sqrt{3}}{1+\sqrt{3+2.1.\sqrt{3}+1}}+\frac{2+\sqrt{3}}{1-\sqrt{3-2.1.\sqrt{3}+1}} \\ =\frac{2-\sqrt{3}}{1+\sqrt{{(\sqrt{3}+1)}^2}}+\frac{2+\sqrt{3}}{1-\sqrt{{(\sqrt{3}-1)}^2}} \\ = \frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1} \\ = \frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}} \\ =\frac{(4-4\sqrt{3}+3)+(3+4\sqrt{3}+3)}{4-1} \\ =\frac{14}{1} \\ =14 \end{gathered}$$

b) Gọi số tiền ông Sáu gửi ban đầu là x( đồng, x > 0).

Theo đề bài ta có:

Số tiền lãi sau 1 năm ông Sáu nhận được là: 0,06x( đồng).

Số tiền có được sau 1 năm của ông Sáu là: x + 0,06x = 1,06x( đồng).

Số tiền lãi năm thứ 2 ông Sáu nhận được là: 1,06x. 0,06 = 0,0636x( đồng).

Do vậy số tiền tổng cộng sau 2 năm ông Sáu nhận được là: 1,06x + 0,0636x = 1,1236x( đồng).

Mặt khác: 1,1236x = 112360000 nên x = 100000000( đồng) hay 100 triệu đồng.

Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.

Bài 4 (1,5 điểm)

a) Ta có:

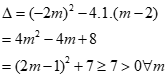
 (1) luôn có 2 nghiệm với mọi m.

b)Theo định lý Viet ta có: $\left\{\begin{array}{l}{x}_1+x_2=2m\\ x_1{x}_2=m-2\end{array}\right.$

Ta có: 

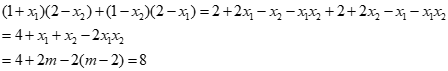
Và 

Do vậy: 

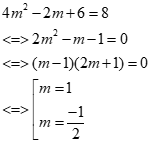
Vậy giá trị của m thỏa mãn là: m = 1; m = $\frac{-1}{2}$

Bài 5 (3,5 điểm)

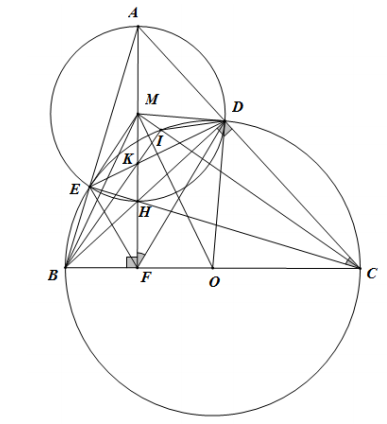
a) Ta có góc BEC = góc BDC = 90^o (góc nội tiếp chắn nửa đường tròn)

Suy ra BD ⊥ AC và CE ⊥ AB . Mà BD cắt CE tại H nên H là trực tâm ∆ ABC.

Suy ra AH ⊥ BC

Vì AH ⊥ BC, BD ⊥ AC nên góc HFC = góc HDC = 90^o

Suy ra góc HFC + góc HDC = 180^o

Suy ra HFCD là tứ giác nội tiếp

⇒ góc HFD = góc HCD

b) Vì M là trung điểm cạnh huyền của tam giác vuông ADH nên MD = MA = MH

Tương tự ta có ME = MA = MH

Suy ra MD = ME

Mà OD = OE nên ∆ OEM = ∆ ODM (c.c.c) ⇒ góc MOE = góc MOD = $\frac{1}{2}$ góc EOD (1)

Theo quan hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = $\frac{1}{2}$ góc EOD (2)

Theo ý a) ta có góc HFD = góc HCD = góc ECD (3)

Từ (1), (2), (3) ⇒ góc MOD = góc HFD hay góc MOD = góc MFD

Suy ra tứ giác MFOD là tứ giác nội tiếp (4)

⇒ góc MDO = 180^o – góc MFO = 90^o ⇒ MD ⊥ DO

Chứng minh tương tự ta có MEFO là tứ giác nội tiếp (5)

Từ (4) và (5) suy ra 5 điểm M, E, F, O, D cùng thuộc 1 đường tròn.

c) Gọi I là giao điểm thứ hai của MC với đường tròn (O)

Ta có góc MDE = góc DCE (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, cùng chắn cung DE) hay góc MDK = góc HCD

Mà góc HCD = góc HFD (cmt) ⇒ góc MDK = góc HFD hay góc MDK = góc MFD

=> tam giác MDK đồng dạng với tam giác MFD(g-g)

Ta có góc MDI = góc MCD (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, cùng chắn cung DI)

=> tam giác MDI đồng dạng với tam giác MCD(g-g)

Xét ∆ MKI và ∆ MCF có

KMI chung 

$\frac{\mathrm{MI}}{\mathrm{MF}}=\frac{\mathrm{MK}}{\mathrm{MC}}$

=> tam giác MKI đồng dạng với tam giác MCF(c-g-c)

⇒ góc MIK = góc MFC = 90^o ⇒ KI ⊥ MC

Mà góc BIC = 90^o (góc nội tiếp chắn nửa đường tròn) nên BI ⊥ MC

Suy ra B, K, I thẳng hàng ⇒ BK ⊥ MC

Mà MK ⊥ BC nên K là trực tâm ∆ MBC.

d) Vì MA = MH nên

Vì MD² = MK. MF (cmt) nên 

Mà MD =MA=> FA .FH =FK .FM

 (đpcm)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2015 - 2016

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Thành phố Hồ Chí Minh có đáp án (Tự luận) - năm 2015

Bài 1: (2 điểm)

Giải các phương trình và hệ phương trình sau:

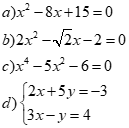
Bài 2: (1,5 điểm)

a) Vẽ đồ thị (P) của hàm số $y=x^2$ và đường thẳng (d): y=x+2 trên cùng một hệ trục toạ độ.

b) Tìm toạ độ các giao điểm của (P) và (d) ở câu trên bằng phép tính.

Bài 3: (1,5 điểm)

Thu gọn các biểu thức sau:

Bài 4: (1,5 điểm)

Cho phương trình $x^2-mx+m-2=0$ (1) (x là ẩn)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m

b) Định m để hai nghiệm x₁;x₂ của (1) thỏa mãn $\frac{{x_1}^2-2}{x_1-1}.\frac{{x_2}^2-2}{x_2-1}=4$

Bài 5: (3,5 điểm)

Cho tam giác ABC (AB<AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại E, F. Gọi H là giao điểm của BE và CF. D là giao điểm của AH và BC.

a) Chứng minh : AD ^ BC và AH.AD=AE.AC

b) Chứng minh EFDO là tứ giác nội tiếp

c) Trên tia đối của tia DE lấy điểm L sao cho DL = DF. Tính số đo góc BLC

d) Gọi R, S lần lượt là hình chiếu của B,C lên EF. Chứng minh DE + DF = RS

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TPHCM NĂM 2015 – 2016

Bài 1: (2 điểm)

Giải các phương trình và hệ phương trình sau:

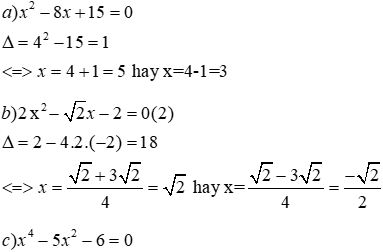
Đặt u = x²$\ge$0 pt thành :

Bài 2:

a)    Đồ thị:

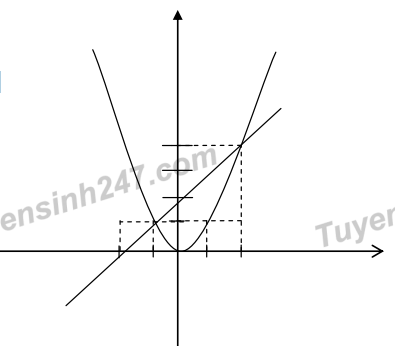
Lưu ý: (P) đi qua O(0;0), (±1;1);(±2;4)

(d) đi qua (-1;1);(2;4)

b) PT hoành độ giao điểm của (P) và (d) là

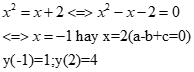
Vậy toạ độ giao điểm của (P) và (d) là (-1;1); (2;4)

Bài 3: Thu gọn các biểu thức sau:

Với x$\ge$0;x$\ne$4 ta có :

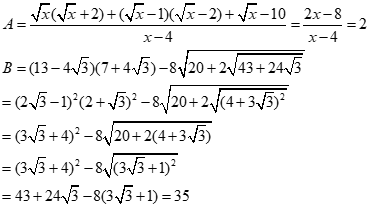
Bài 4:

Cho phương trình x²- mx + m - 2 = 0  (1)   (x là ẩn số)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m

Vậy phương trình có 2 nghiệm phân biệt với mọi m

b) Định m để hai nghiệm x₁;x₂ của (1) thỏa mãn $\frac{{x_1}^2-2}{x_1-1}.\frac{{x_2}^2-2}{x_2-1}=4$

Vì a+b+c = 1-m+m-2 = -1 $\ne$0$\forall m$ nên phương trình (1) có 2 nghiệm $x_1;x_2\ne 1$

Từ (1) suy ra : $x^2-2=mx-m$

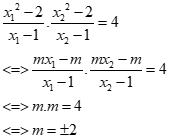
Bài 5

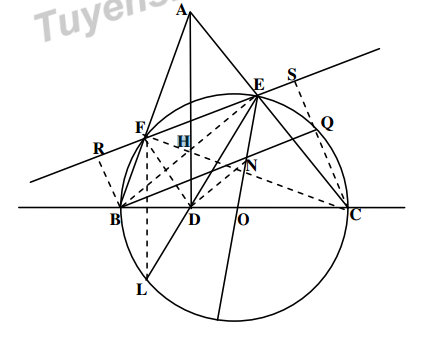
a)Do FC ^AB ,BE ^AC $\Rightarrow$ , H trực tâm $\Rightarrow$ AH^ BC

Ta có tứ giác HDCE nội tiếp

Xét 2 tam giác đồng dạng EAH và DAC (2 tam giác vuông có góc A chung)

$\frac{AH}{AC}=\frac{AE}{AD}\Rightarrow AH.AD=AE.AC$(đpcm)

b)Do AD là phân giác của FDE nên FDE= 2FBE= 2FCE= FOE

Vậy tứ giác EFDO nội tiếp (cùng chắn cung EF )

c)Vì AD là phân giác FDE Þ DB là phân giác FDL

$\Rightarrow$F, L đối xứng qua BC $\Rightarrow$ L$\in$ đường tròn tâm O

Vậy BLC là góc nội tiếp chắn nửa đường tròn tâm O $\Rightarrow$ = BLC 90⁰

d) Gọi Q là giao điểm của CS với đường tròn O.

Vì 3 cung BF, BL và EQ bằng nhau (do kết quả trên)

=>Tứ giác BEQL là hình thang cân nên hai đường chéo BQ và LE bằng nhau.

Mà BQ = RS, LE = DL + DE = DF + DE suy ra điều phải chứng minh.