Đề thi vào 10 môn Toán Tỉnh Quảng Ninh chính thức (2022) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh chính thức (2022 + các năm) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2022

ĐÁP ÁN

Câu 1.

a) $2\sqrt{9}-\sqrt{4}$ = 2.3 - 3 = 2

b)

 $$\begin{gathered} A=({\displaystyle \frac{1}{\sqrt{x}-1}}+{\displaystyle \frac{1}{\sqrt{x}+1}}):{\displaystyle \frac{2}{x-1}} \\ =({\displaystyle \frac{\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}}+{\displaystyle \frac{(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+1)}}):{\displaystyle \frac{2}{x-1}} \\ ={\displaystyle \frac{2\sqrt{x}}{x-1}}.{\displaystyle \frac{x-1}{2}}=\sqrt{x} \end{gathered}$$

Vậy A = $\sqrt{x}$

c) Đường thẳng (d): y = 2x + 3m đi qua điểm B(1;5)

hay 5 = 2.1 + 3m ⇔ 3m = 3 ⇔ m = 1

Vậy với m = 1 là giá trị cần tìm.

d) $\{\begin{array}{c}2x-y=7\hfill \\ x+y=2\hfill \end{array}$ ⇔$\{\begin{array}{c}3x=9\hfill \\ x+y=2\hfill \end{array}$

⇔$\{\begin{array}{c}x=3\hfill \\ x+y=2\hfill \end{array}$⇔$\{\begin{array}{c}x=3\hfill \\ y=-1\hfill \end{array}$

Vậy ....

Câu 2:

Câu 3:

Câu 4:

Câu 5: 

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2021 - 2022

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2021

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2020 - 2021

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2020

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2019 - 2020

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2019

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2016 - 2017

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2016

Bài 1 (2,5 điểm)

1. Rút gọn biểu thức:

a) $A=\sqrt{12}-\sqrt{3}$

b) $B =\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2\sqrt{x}}{x-1}-\frac{1}{\sqrt{x}+1}$ với $x\ge 0$ và $x\ne 1$ 

2. Giải phương trình: $x^2-x-2=0$ 

Bài 2. (1,5 điểm)

1. Giải hệ phương trình: $\left\{\begin{array}{l}x+2y=-3\\ x-y=3\end{array}\right.$ 

2. Tìm giá trị của m để hai đường thẳng $\left(d_1\right): mx+y=1$ và $\left(d_2\right): x-my=m+6$ cắt nhau

tại một điểm M thuộc đường thẳng 4 (d): x+2y=8 

Bài 3. (2,0 điểm)

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Theo kế hoạch, một người công nhân phải hoàn thành 84 sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật, nên thực tế mỗi giờ người đó đã làm được nhiều hơn 2

sản phẩm so với số sản phẩm phải làm trong một giờ theo kế hoạch. Vì vậy, người đó

hoàn thành công việc sớm hơn dự định 1 giờ. Hỏi theo kế hoạch, mỗi giờ người công

nhân phải làm bao nhiêu sản phẩm ?

Bài 4. (3,5 điểm)

Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không

trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy

điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E.

a) Chứng minh tứ giác BDEH nội tiếp

b) Chứng minh $A{C}^2=AE.AD$ 

c) Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB

tại F khác B. Chứng minh EF // AB.

Bài 5. (0,5 điểm)

Với x, y là các số thực dương thỏa mãn điều kiện x + y + xy = 15. Tìm giá trị nhỏ nhất

của biểu thức P = x² + y².

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH QUẢNG NINH NĂM 2016-2017

Bài 1. (2,5 điểm)

1. Rút gọn biểu thức:

a) 

b) $B =\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2\sqrt{x}}{x-1}-\frac{1}{\sqrt{x}+1}$ với $x\ge 0$ và $x \ne 1$

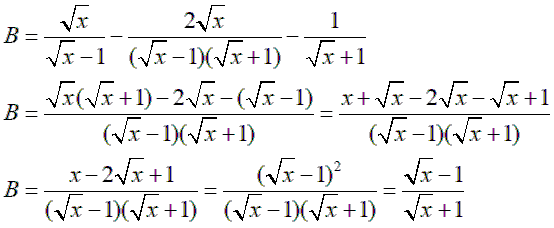
2. Giải phương trình $x^2-x-2=0$ 

Ta có a-b+c = 0

Phương trình có 2 nghiệm phân biệt:

x₁ = -1 , x₂ = 2

Bài 2. (1,5 điểm)

1. Giải hệ phương trình: $\left\{\begin{array}{l}x+2y=-3\\ x-y=3\end{array}\right.$

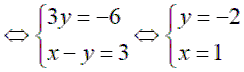
Hệ phương trình có nghiệm duy nhất (1; -2)

 2. Tìm giá trị của m để hai đường thẳng $\left(d_1\right): mx+y=1$ và $\left(d_2\right): x-my=m+6$ cắt

nhau tại một điểm M thuộc đường thẳng 4 (d): x+2y=8 

Để hai đường thẳng (d₁), (d₂) cắt nhau thì  luôn T/M với mọi m.

(d): x + 2y = 8 => x = 8 - 2y                      (1)

                (2)

Do đó  

$\iff x^2-6x+y^2-1=0$ (3)

Thay (1) vào (3) ta được tung độ giao điểm M là nghiệm PT:

(8 – 2y)² – 6(8-2y) + y² = 1 ó 5y² – 20y + 15 = 0

=> y₁ = 1 hoặc y₂ = 6

Với y₁ = 1 => x₁ = 6 thay (6; 1) vào (2) ta được m = 0 (TMĐK)

Với y₂ = 3 => x₂ = 2 thay (2; 3) vào (2) ta được m = -1(TMĐK)

Vậy với m = 0 hoặc m = -1 thì hai đường thẳng (d₁) và (d₂) cắt nhau tại một điểm M

thuộc đường thẳng (d)

Bài 3. (2,0 điểm)

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Theo kế hoạch, một người công nhân phải hoàn thành 84 sản phẩm trong một thời gian

nhất định. Do cải tiến kĩ thuật, nên thực tế mỗi giờ người đó đã làm được nhiều hơn 2

sản phẩm so với số sản phẩm phải làm trong một giờ theo kế hoạch. Vì vậy, người đó

hoàn thành công việc sớm hơn dự định 1 giờ. Hỏi theo kế hoạch, mỗi giờ người công

nhân phải làm bao nhiêu sản phẩm ?

Gọi x là số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo kế hoạch

(sp/h, x Є N*, x < 84)

Theo bài ra ta có:

Số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo thực tế: x+2 (sp/h)

Thời gian mà công nhân hoàn thành theo kế hoạch: $\frac{84}{x}$ (h)

Thời gian mà công nhân hoàn thành theo thực tế: $\frac{84}{x+2}\left(h\right)$

Người công nhân đó hoàn thành công việc sớm hơn định 1h nên ta có phương trình: $\frac{84}{x}-\frac{84}{x+2}=1$

Giải phương trình ta được: x₁ = 12 (TMĐK) ; x₂ = -14 (KTMĐK)

Vậy theo kế hoạch mỗi giờ người công nhân phải làm 12 sản phẩm.

Bài 4. (3,5 điểm)

Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E.

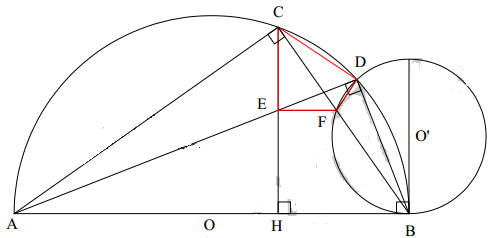
a) Chứng minh tứ giác BDEH nội tiếp

Xét (O) ta có:  (góc nội tiếp chắn nửa đường tròn) hay 

GT => hay 

Xét tứ giác BDEH có  

mà  hai góc đối

⇒ Tứ giác BDEH nội tiếp (đpcm).

b) Chứng minh $A{C}^2=AE.AD$ 

Xét ∆ AEH và ∆ ABD có:

$\hat{A}$ chung

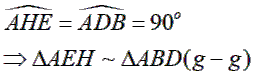
 (1)

(góc nội tiếp chắn nửa đường tròn)

Xét ∆ vuông AEH có CH là đường cao

Ta có : $A{C}^2=AH.AB$ (hệ thức lượng trong ∆ vuông)          (2)

(1), (2) => $A{C}^2=AE.AD$ (đpcm)

c) Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB

Tại F khác B. Chứng minh EF // AB.

Ta có:  (hệ quả góc tạo bởi tia tiếp tuyến và dây cung)

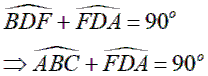
Mặt khác  (vì cùng phụ với góc HCB)

Lại có 

 hay  

Xét tứ giác ECDF có 

mà C, D là hai đỉnh liên tiếp

⇒ tứ giác ECDF nội tiếp (dấu hiệu nhận biết)

 hay  (góc nội tiếp do cùng chắn cung FD)

mà  (góc nội tiếp cùng chắn cung DB)

Hai góc ở vị trí đồng vị

⇒ EF//AB (đpcm)

Bài 5. (0,5 điểm)

Với x, y là các số thực dương thỏa mãn điều kiện x + y + xy = 15. Tìm giá trị nhỏ nhất

của biểu thức

P = x² + y².

Vì x, y là những số thực dương nên theo BĐT Côsi ta có

 dấu “=” xảy ra khi x = y hay  

GT:  

Do đó:

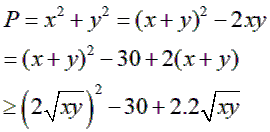
dấu “=” xảy ra khi x = y = 3

 tại x = y = 3

Đáp án chỉ nêu sơ lược cánh giải

Các bạn phải trình bày chi tiết mới được điểm tối đa

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2015 - 2016

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Quảng Ninh có đáp án - năm 2015

Bài 1: (2,0 điểm)

1.    Tìm x biết

a)  x – 2015 = 0

b) x² – 5x + 6 = 0

c)  

2. Cho x > 0, x hãy rút gọn biểu thức:

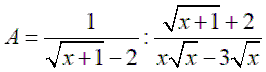
Bài 2 (2,0 điểm)

Cho phương trình chứa tham số m

Tìm m để phương trình có hai nghiệm x₁; x₂ và hai nghiệm đó thoả mãn điều kiện: 

Bài 3: (2,0 điểm)

Hàng ngày, Nam đạp xe đi học với vận tốc không đổi trên quãng đường dài 10 km.

Nam tính toán và thấy rằng đạp xe với vận tốc lớn nhất thì thời gian đi học sẽ rút ngắn

10 phút so với đạp xe với vận tốc hằng ngày. Tuy nhiên, thực tế sáng nay lại khác dự

kiến. Nam chỉ đạp xe với vận tốc lớn nhất trên nửa đầu quãng đường (dài 5km), nửa

quãng đường còn lại đường phố đông đúc nên Nam đã đạp xe với vận tốc hàng ngày.

Vì vậy thời gian đạp xe đi học sáng nay của Nam là 35 phút. Hãy tính vận tốc đạp xe

hàng ngày và vận tốc đạp xe lớn nhất của Nam (lấy đơn vị vận tốc là km/h)

Bài 4 : (3,5 điểm)

Cho đường tròn tâm O bán kính OA. Điểm C thuộc đoạn thẳng AO (C khác A và O).

Đường thẳng vuông góc với AO tại C cắt đường tròn (O) tại hai điểm D và K. Tiếp

tuyến tại D của đường tròn (O) cắt đường thẳng AO tại E. Tiếp tuyến tại A của đường

tròn (O) cắt đường thẳng DE tại F. Gọi H là giao điểm của hai đường thẳng FO và DK.

1. Chứng minh các tứ giác AFDO và AHOK là tứ giác nội tiếp

2. Chứng minh đường thẳng AH song song với đường thẳng ED

3. Chứng minh đẳng thức DH² = EF.CH

Bài 5: (0,5 điểm)

Cho các số thực dương a và b thoả mãn 2a + b . Tìm giá trị nhỏ nhất của biểu thức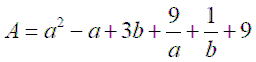 

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH QUẢNG NINH NĂM 2015-2016

Bài 1:

1. Tìm x:

a. x – 2015 = 0

x=2015

b.    x² – 5x + 6 = 0

$∆$= (-5)² – 4.1.6 = 1> 0

Phương trình có 2 nghiệm phân biệt: 

c.

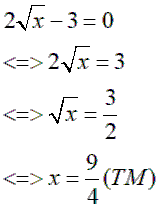
2.

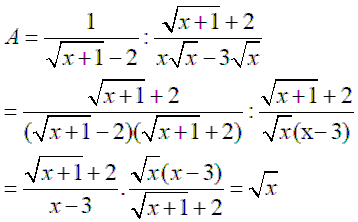
Bài 2:

Để phương trình có hai nghiệm x₁, x₂ thì = (-m-1)² – (2m +1) = m² thỏa mãn với mọi

m thuộc R

Theo viet ta có: x₁ + x₂ = 2(m+1) (2)

x₁.x₂ = 2m +1 (3)

Thay (2), (3) vào (1) ta có:

4(m+1)² – (2m+1)² – 6m > 4

$\iff$4m² + 8m + 4-4m² – 4m – 1 – 6m – 4 > 0

$\iff$-2m – 1 > 0

$\iff m<\frac{-1}{2}$

Bài 3:

Gọi vận tốc đạp xe hằng ngày của Nam là x (km/h, x > 0)

Vận tốc đạp xe lớn nhất của Nam là y (km/h, y > x)

Thời gian đi hàng ngày của Nam từ nhà đến trường là $\frac{10}{x}$(h)

Thời gian đi của Nam từ nhà đến trường với vận tốc lớn nhất là $\frac{10}{y}$ (h)

Theo bài ra Nam tính toán và thấy rằng nếu đạp xe với vận tốc lớn nhất thì thời gian đi học sẽ rút ngắn 10 phút ($\frac{1}{6}\left(h\right)$)  nên ta có pt: $\frac{10}{x}-\frac{10}{y}=\frac{1}{6}$

Thời gian đi học thực tế của Nam trong 5 km đầu là $\frac{5}{y}\left(h\right)$

Thời gian đi học thực tế của Nam trong 5 km cuối là $\frac{5}{x}\left(h\right)$

Theo bài ra vì thời gian đạp xe đi học sáng nay của Nam là 35 phút

($\frac{7}{12}\left(h\right)$)nên ta có phương trình $\frac{5}{x}+\frac{5}{y}=\frac{7}{12}$

Giải hệ pt:

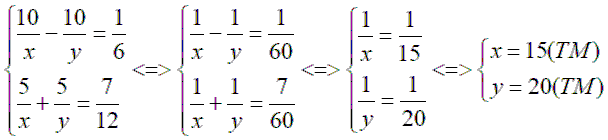
Vậy vận tốc đạp xe hàng ngày của Nam là 15 (km/h)

Vận tốc đạp xe lớn nhất của Nam là 20 (km/h)

Bài 4 (3,5 điểm)

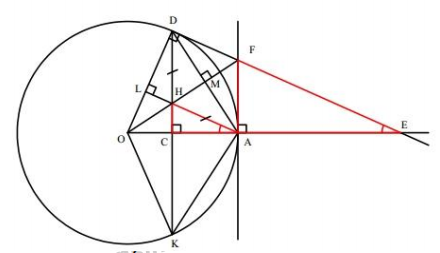
1. Chứng minh các tứ giác nội tiếp:

- Chứng minh các tứ giác AFDO nội tiếp

Theo gt suy ra DE và AF là hai tiếp tuyến OD 

Xét tứ giác ODFA có ODF+OAF=180^o

Mà ODF và OAFlà 2 góc đối nhau=>tứ  giác AFDO nội tiếp(đpcm)

- Chứng minh các tứ giác AHOK nội tiếp

Theo tính chất 2 tiếp tuyến cắt nhau ta có FD = FA mà OD = OA = R

=>OF là đường trung trực của AD (định lý đảo đường trung trực)

=>OF$\perp$ DA =>OM là đường cao (M = OF giao DA)

Xét tam giác ODA có DC và OM là hai đường cao=> H là trực tâm

=>AH$\perp$ OD hay AL$\perp$OD (tính chất ba đường cao trong tam giác) (2)

Xét tứ giác OLHC có OLH+OCH=180^o

Mà : LOC+LHC+OLH+OCH=360^o

=>LOC+LHC=180^o  (3)

Mà  LHC+CHA=180^o (hai góc kề bù)   (4)

Từ (3);(4) => LOC=CHA hay LOC=AHK(5)

Mặt khác xét tam giác DOK có OD = OK = R nên tam giác DOK cân tại O

Lại có OA$\perp$ DK (gt) hay OC$\perp$DK (C thuộc OA)

=>CO đồng thời là đường cao đồng thời là phân giác tam giác cân DOK

=>LOC=KOC hay LOC=KOA(6)

Từ (5);(6) =>AHK=KOA

Do đó điểm H, O liên tiếp nhau cùng nhìn AK một góc không đổi

=> Tứ giác AHOK là tứ giác nội tiếp (đpcm)

2. Chứng minh đường thẳng AH song song với đường thẳng ED

OD$\perp$ DE (theo (1)); OD$\perp$ AL (theo (2)) AL // DE hay AH // DE (H thuộc AL) (từ

vuông góc đến song song) (đpcm)

3. Chứng minh đẳng thức DH² = EF.CH

Theo cmt ta có OF là trung trực của DA mà H thuộc OF nên DH = AH (định lý trung

trực) (7)

DC$\perp$ OA, FA$\perp$ OE =>DC // FA

Mà AH // ED (cm ý 1)

=> Tứ giác DFAH là hình bình hành DH = AF (tc hình bình hành) (8)

Xét tam giác CHA và tam giác AFE có HCA=FAE=90^o

Lại có : CAH=AEF(2 góc đồng vị do AH//DE cmt)

=> Tam giác CHA đồng dạng với tam giác AFE

=>Kết hợp (7),(8) DH² = EF.CH (đpcm)

Bài 5:

Xét 

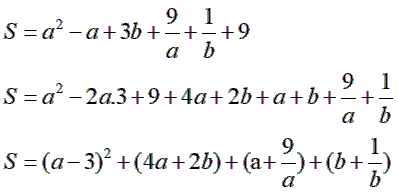
Trong đó:

(a-3)² $\ge 0,$dấu “=” xảy ra khi a = 3

$4a+2b\ge 14$ do 2a+b$\ge$7(gt) dấu “=” xảy ra khi a = 3, b = 1

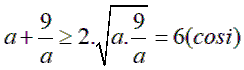 dấu “=” xảy ra khi 

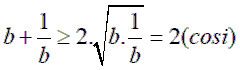 dấu “=” xảy ra khi 

Do đó S $⩾$0 + 14+6+2 =>S$\ge$22 dấu “=” xảy ra khi a = 3, b = 1

Vậy Min S = 22 khi a = 3, b = 1