Đề thi vào 10 môn Toán TP Hà Nội chính thức (2022) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi vào 10 môn Toán TP Hà Nội chính thức (2022 + các năm) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2022

ĐÁP ÁN CHÍNH THỨC 2022

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2021 - 2022

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2021

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2020 - 2021

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2020

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2019 - 2020

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2019

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2016 - 2017

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2016

Bài 1 (2,0 điểm)

Cho hai biểu thức $A=\frac{7}{\sqrt{x}+8}$ và $B=\frac{\sqrt{x}}{\sqrt{x}-3}+\frac{2\sqrt{x}-24}{x-9}$  với x ≥ 0, x ≠ 9

1) Tính giá trị của biểu thức A khi x = 25

2) Chứng minh $B=\frac{\sqrt{x}+8}{\sqrt{x}+3}$

3) Tìm x để biểu thức P = A.B có giá trị là số nguyên

Bài 2 (2,0 điểm)

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Một mảnh vườn hình chữ nhật có diện tích 720 m². Nếu tăng chiều dài thêm 10m và giảm chiều rộng 6m thì diện tích mảnh vườn không đổi. Tính chiều dài và chiều rộng của mảnh vườn.

Bài 3 (2,0 điểm)

1) Giải hệ phương trình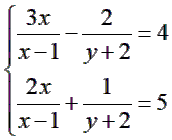 

2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = 3x + m – 1 và parabol (P): y = x²

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m

b) Gọi x₁, x₂ là hoành độ các giao điểm của (d) và (P). Tìm m để (x₁+1)(x₂+1)=1

Bài 4 (3,5 điểm)

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm) và đường kính BC. Trên đoạn thẳng CO lấy điểm I (I khác C, I khác O). Đường thẳng AI cắt (O) tại hai điểm D và E (D nằm giữa A và E). Gọi H là trung điểm của đoạn thẳng DE.

1) Chứng minh bốn điểm A, B, O, H cùng nằm trên một đường tròn.

2) Chứng minh $\frac{AB}{AE}=\frac{BD}{BE}$

3) Đường thẳng d đi qua điểm E song song với AO, d cắt BC tại điểm K. Chứng minh HK // DC

4) Tia CD cắt AO tại điểm P, tia EO cắt BP tại điểm F. Chứng minh tứ giác BECF là hình chữ nhật.

Bài 5 (0,5 điểm)

Với các số thực x, y thỏa mãn  tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x + y

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TP HÀ NỘI NĂM 2016 – 2017

Bài 1.(2,0 điểm)

1) x = 25 nên ta có: $\sqrt{x}=5$

Khi đó ta có: $A=\frac{7}{5+8}=\frac{7}{13}$

2)

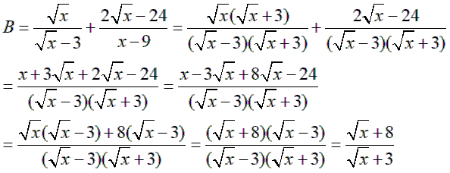
3)    P = A.B nên ta có: 

+) Ta có x $\ge$0 nên P > 0

+) x ³ 0 => $\sqrt{x}+3 \ge 3 \iff \frac{7}{\sqrt{x}+3}\le \frac{7}{3}$

Nên : $0<P\le \frac{7}{3}$

Để P$\in$Z =>P$\in${1;2}

+)P = 1 <=> x=16 (thỏa mãn điều kiện)

+) P = 2 <=>x=$\frac{1}{4}$(thỏa mãn điều kiện)

Vậy x$\in${$\frac{1}{4}$;16}

Bài 2 (2 điểm). Giải bài toán bằng cách lập phương trình, hệ phương trình

Gọi chiều rộng của mảnh vườn hình chữ nhật là x (x>0; đơn vị: m)

Vì diện tích của của mảnh vườn hình chữ nhật là 720 m² nên chiều dài là: $\frac{720}{x}$(m)

Sau khi thay đổi kích thước:

Chiều rộng của của mảnh vườn hình chữ nhật là: x – 6 (m)

Chiều dài của của mảnh vườn hình chữ nhật là: $\frac{720}{x}$+10(m)

Vì diện tích của của mảnh vườn hình chữ nhật không đổi nên ta có phương trình:

(x-6).( $\frac{720}{x}$+10)=720

=>(x-6)(72+x)=72x

<=>x²-6x-432=0

Phương trình có hai nghiệm phân biệt: x₁=24 (thỏa mãn điều kiện); x₂=-18 (loại)

Vậy chiều rộng mảnh đất hình chữ nhật đó là 24 m; chiều dài mảnh đất hình chữ nhật đó là: 720:24 = 30 (m)

Bài 3 ( 2 điểm)

1)    Giải hệ phương trình

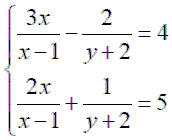 ĐK x $\ne$1; y$\ne$ -2

Đặt 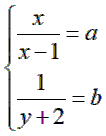(b ≠ 0)Khi đó hệ phương trình trở thành: 

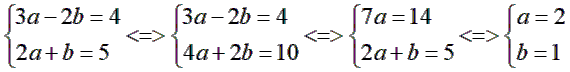
Khi đó ta có: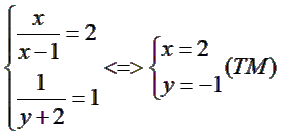 

Vậy hệ phương trình có 1 nghiệm duy nhất (2;-1)

2) Trong mặt phẳng tọa độ Oxy cho đường thẳng  (d): y=3x + m² – 1 và parabol (P): y= x².

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m

Xét phương trình hoành độ giao điểm của (d) và (P):

x²=3x+m²-1

<=>x²-3x-m²+1=0(*)

$∆={(-3)}^2-4.1.(-m^2+1)=4m^2+5>0$

<=>Phương trình (*) luôn có hai nghiệm phân biệt với mọi m

<=>(d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

b) Gọi x₁; x₂ là hoành độ các giao điểm của (d) và (P). Tìm m để  (x₁+1)(x₂+1)=1

Ta có:

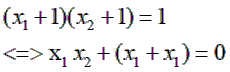
Áp dụng hệ thức Vi-et cho (*):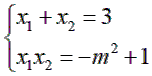 

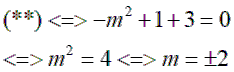
Vậy m=$\pm 2$

Bài 4 (3,5 điểm)

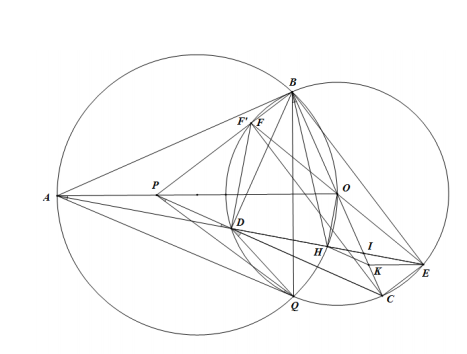
1) Vì AB là tiếp tuyến của (O) nên AB ⊥ BO ⇒ góc ABO = 90^o

Vì H là trung điểm của dây DE của (O) nên OH ⊥ DE ⇒ góc AHO = 90^o

Suy ra góc ABO + góc AHO = 180^O ⇒ AHOB là tứ giác nội tiếp

Suy ra bốn điểm A, H, O, B nằm trên cùng một đường tròn.

2) Có góc ABD = góc AEB (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BD)

Xét ∆ ABD và ∆ AEB có chung góc BAE, góc ABD = góc AEB nên

Tam giác ABD đồng dạng với tam giác AEB(g-g)=> $\frac{AB}{AE}=\frac{BD}{EB}$

3) Vì ABOH là tứ giác nội tiếp nên góc OAH = góc OBH

Vì EK // AO nên góc OAH = góc HEK

Suy ra góc OBH = góc HEK ⇒ BHKE là tứ giác nội tiếp ⇒ góc KHE = góc KBE

Vì BDCE là tứ giác nội tiếp nên góc KBE = góc CDE

Suy ra góc KHE = góc CDE ⇒ KH // CD

4) Gọi F’ là giao điểm của BP và đường tròn (O).

Gọi AQ là tiếp tuyến thứ 2 của (O)

Vì BDQC là tứ giác nội tiếp nên góc QDC = góc QBC(1)

Vì ABOQ là tứ giác nội tiếp đường tròn đường kính AO nên góc QBC = góc QAO (2)

Từ (1), (2) ⇒ góc QDC = góc OAQ ⇒ APDQ là tứ giác nội tiếp

⇒ góc PDA = góc PQA (3)

Có góc PDA = góc EDC = góc EBC (4)

Ta có ∆ ABP = ∆ AQP (c.g.c) ⇒ góc PQA = góc PBA (5)

Từ (3), (4), (5) ⇒ góc PBA = góc EBC

Suy ra góc PBE = góc ABC = 90^o ⇒ góc F’BE = 90^o ⇒ F’E là đường kính của (O)

⇒ F’ ∈ OE ⇒ F’ ≡ F

Vì FBEC là tứ giác nội tiếp nên góc FCE = 180$°$– góc FBE = 90$°$

Tứ giác FBEC có góc FCE = góc FBE = góc BEC = 90$°$ nên là hình chữ nhật.

Bài 5 (0,5 điểm)

Điều kiện: x ≥ –6, y ≥ –6

Từ điều kiện đề bài ta có x + y ≥ 0 và 

(*)

Áp dụng bất đẳng thức Côsi cho hai số không âm, ta có

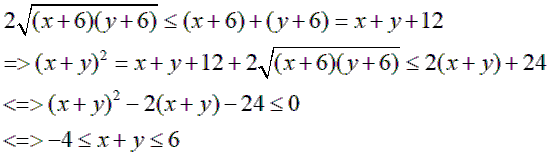
Khi x = y = 3 thì x + y = 6

Ta có $2\sqrt{(x+6)(y+6)}\ge 0$ nên từ (*) suy ra

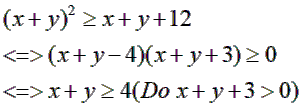
Khi x = 10, y = –6 hoặc x = –6, y = 10 thì x + y = 4

Vậy GTLN của P là 6 khi x = y = 3 và GTNN của P là 4 khi x = 10, y = –6 hoặc x = –6, y = 10

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2015 - 2016

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hà Nội - năm 2015

Bài 1 (2,0 điểm)

Cho hai biểu thức $P=\frac{x+3}{\sqrt{x}-2}$ và $Q=\frac{\sqrt{x}-1}{\sqrt{x}+2}+\frac{5\sqrt{x}-2}{x-4}$  với x>0, x $\ne$ 4

1) Tính giá trị của biểu thức P khi x = 9.

2) Rút gọn biểu thức Q.

3) Tìm giá trị của x để biểu thức $\frac{P}{Q}$ đạt giá trị nhỏ nhất.

Bài 2 (2,0 điểm) Giái bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Một tàu tuần tra chạy ngược dòng 60km, sau đó chạy xuôi dòng 48km trên cùng một dòng sông có vận tốc của dòng nước là 2km/giờ. Tính vận tốc của tàu tuần tra khi nước yên lặng, biết thời gian xuôi dòng ít hơn thời gian ngược dòng 1 giờ.

Bài 3 (2,0 điểm)

1) Giải hệ phương trình $\left\{\begin{array}{l}2(x+y)+\sqrt{x+1}=4\\ (x+y)-3\sqrt{x+1}=-5\end{array}\right.$

2) Cho phương trình : x²-(m+5)x+3m+6=0 (x là ẩn số).

a. Chứng minh phương trình luôn có nghiệm với mọi số thực m.

b. Tìm m để phương trình có hai nghiệm x₁, x₂ là độ dài hai cạnh góc vuông của một tam giác có độ dài cạnh huyền bằng 5.

Bài 4 (3,5 điểm) Cho nửa đường tròn tâm O có đường kính AB. Lấy điểm C trên

đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung KB (M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai N.

1) Chứng minh tứ giác ACMD là tứ giác nội tiếp.

2) Chứng minh CA.CB=CH.CD.

3) Chứng minh ba điểm A, N, D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DH.

4) Khi M di động trên cung KB, chứng minh đường thẳng MN luôn đi qua một điểm cố định.

Bài 5 (0,5 điểm) Với hai số thực không âm a, b thỏa mãn a²+b²=4, tìm giá trị lớn nhất của biểu thức: $M=\frac{ab}{a+b+2}$

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TP HÀ NỘI NĂM 2015-2016

Bài 1 (2,0 điểm)

1) Với x = 9 ta có $P=\frac{9+3}{3-2}=12$

2) Với $Q=\frac{\sqrt{x}-1}{\sqrt{x}+2}+\frac{5\sqrt{x}-2}{x-4}=\frac{(\sqrt{x}-1)(\sqrt{x}-2)+5\sqrt{x}-2}{x-4}$

$=\frac{x-3\sqrt{x}+2+5\sqrt{x}-2}{x-4}=\frac{x+2\sqrt{x}}{x-4}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}+2)(\sqrt{x}-2)}=\frac{\sqrt{x}}{\sqrt{x}-2}$

$3) \frac{P}{Q}=\frac{x+3}{\sqrt{x}}=\sqrt{x}+\frac{3}{\sqrt{x}}\ge 2\sqrt{3}$ (Do bất đẳng thức Cosi).

Dấu bằng xảy ra khi $\sqrt{x}=\frac{3}{\sqrt{x}}<=>x=3$

Vậy giá trị nhỏ nhất của $\frac{P}{Q}$ là $2\sqrt{3}$

Bài 2 (2,0 điểm)

Gọi t₁ là thời gian tàu tuần tra chạy ngược dòng nước.

Gọi t₂ là thời gian tàu tuần tra chạy xuôi dòng nước.

Gọi V là vận tốc của tàu tuần tra khi nước yên.

Ta có:

 $\begin{array}{l}V-2=\frac{60}{t_1};V+2=\frac{48}{t_2}\\ =>\frac{60}{t_1}+2=\frac{48}{t_2}-2<=>\frac{60}{t_1}-\frac{48}{t_2}=-4\left(1\right)\\ t_1-t_2=1\left(2\right)\\ \left(1\right);\left(2\right)<=>\left\{\begin{array}{l}\frac{60}{t_1}-\frac{48}{t_2}=-4\\ t_1-t_2=1\end{array}\right.<=>\left\{\begin{array}{l}\frac{60}{t_1}-\frac{48}{t_2}=-4\\ t_1=1+t_2\end{array}\right.\\ <=>\frac{60}{1+t_2}-\frac{48}{t_2}=-4<=>4{t_2}^2+16t_2-48=0\\ <=>\left[\begin{array}{l}{t}_2=-6\left(L\right)\\ t_2=2\left(TM\right)=>V=22(km/h)\end{array}\right.\end{array}$

Bài 3 (2,0 điểm)

1) Với điều kiện x $\ge -$1, ta có hệ đã cho tương đương:

$\begin{array}{l}\left\{\begin{array}{l}6(x+y)+3\sqrt{x+1}=12\\ (x+y)-3\sqrt{x+1}=-5\end{array}\right.<=>\left\{\begin{array}{l}7(x+y)=7\\ (x+y)-3\sqrt{x+1}=-5\end{array}\right.\\ <=>\left\{\begin{array}{l}x+y=1\\ 3\sqrt{x+1}=6\end{array}\right.<=>\left\{\begin{array}{l}x+y=1\\ x+1=4\end{array}\right.<=>\left\{\begin{array}{l}x=3\\ y=-2\end{array}\right.\end{array}$

2)

a) $\Delta ={(m+5)}^2-4(3m+6)=m^2-2m+1={(m-1)}^2\ge 0\forall m$

Do đó, phương trình luôn có nghiệm với mọi m.

b) Ta có $\left\{\begin{array}{l}{x}_1+x_2=m+5\\ x_1{x}_2=3m+6\end{array}\right.$

Để x₁>0; x₂>0 điều kiện là m>-5 và m> -2 <=> m>-2( Điều kiện để S>0; P>0)

Yêu cầu bài toán tương đương :

$\begin{array}{l}{x_1}^2+{x_2}^2=25<=>-2x_1{x}_2=25\\ <=>-2(3m+6)=25\left(Do\left\{\begin{array}{l}{x}_1+x_2=m+5\\ x_1{x}_2=3m+6\end{array}\right.\right)\\ <=>m^2+4m-12=0,m>-2\\ <=>m=2\text{ hay m=-6,m>-2}\\ \text{<=>m=2}\end{array}$

Bài 4 (3,5 điểm)

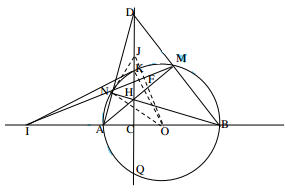
1) Tứ giác ACMD có ACD=AMD= 90^o Nên tứ giác ACMD nội tiếp

2) Xét 2 tam giác vuông : DACH và DDCB đồng dạng

(Do có CDB =MAB  (góc có cạnh thẳng góc))

Nên ta có: $\frac{CA}{CH}=\frac{CD}{CB}=>CA.CB=CH.CD$

3) Do H là trực tâm của DABD

Vì có 2 chiều cao DC và AM giao nhau tại H , nên AD ^ BN

Hơn nữa ANB = 90⁰ vì chắn nửa đường tròn đường kính AB.

Nên A, N, D thẳng hàng.

Gọi tiếp tuyến tại N cắt CD tại J ta chứng minh JND=NDJ.

Ta có JND=NBA cùng chắn cung AN .

Ta có NDJ =NBA góc có cạnh thẳng góc

$\Rightarrow$JND=NDJ.Vậy trong tam giác vuông DDNH J là trung điểm của HD.

4) Gọi I là giao điểm của MN với AB. CK cắt đường tròn tâm O tại điểm Q.

Khi đó JM, JN là tiếp tuyến của đường tròn tâm O.

Gọi F là giao điểm của MN và JO. Ta có KFOQ là tứ giác nội tiếp.

=>FI là phân giác KFQ.

Ta có: $KFQ=KOQ=>KFI=FOI$

=>tứ giác KFOI nội tiếp

$=>IKO={90}^o$=>IK là tiếp tuyến đường tròn tâm O

Vậy MN đi qua điểm cố định I (với IK là tiếp tuyến của đường tròn tâm O)

Bài 5 (0,5 điểm)

$\begin{array}{l}M=\frac{ab}{a+b+2}=\frac{{(a+b)}^2-(a^2+b^2)}{2(a+b+2)}\\ =\frac{{(a+b)}^2-4}{2(a+b+2)}\\ =\frac{(a+b+2)(a+b-2)}{2(a+b+2)}\\ =\frac{a+b-2}{2}\end{array}$

Ta có: ${(a+b)}^2\le 2(a^2+b^2)<=>a+b\le \sqrt{2(a^2+b^2)}$

Vậy $M\le \frac{\sqrt{2(a^2+b^2)}-2}{2}=\frac{\sqrt{2.4}-2}{2}=\sqrt{2}-1$

Khi a=b=$\sqrt{2}$ thì M=$\sqrt{2}$-1. Vậy giá trị lớn nhất của M là $\sqrt{2}$-1