Đề thi vào 10 môn Toán TP Hải Phòng chính thức (2022) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi vào 10 môn Toán TP Hải Phòng chính thức (2022 + các năm) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hải Phòng có đáp án - năm 2022

ĐÁP ÁN

Bài 1:

Bài 2:

Bài 3:

Bài 4: 

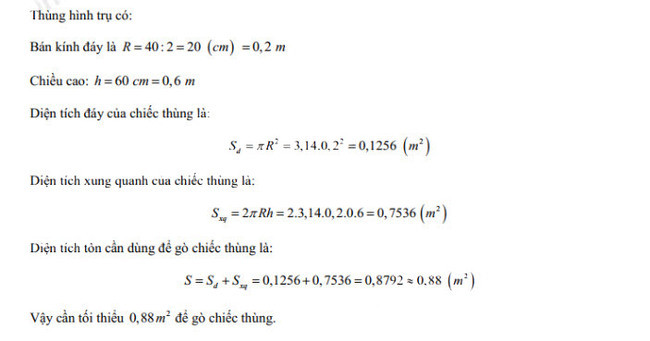
Bài 5:

Bài 6:

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2021 - 2022

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hải Phòng có đáp án - năm 2021

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2020 - 2021

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hải Phòng có đáp án - năm 2020

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2016 - 2017

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hải Phòng có đáp án - năm 2016

I. Phần 1. Trắc nghiệm (2,0 điểm)

Hãy chọn chỉ một chữ cái đứng trước câu trả lời đúng

Bài 1: Biểu thức $\sqrt{\frac{x}{2016}}$ xác định khi và chỉ khi

A. $x\ge 0$

B. x < 0

C. x > 0

D. x = 0

Bài 2: Đồ thị hàm số y = 2x – 5 không đi qua điểm nào dưới đây?

A. (1;-3)                          

B. (-1;-3)                                

C. (2;-1)                                   

D. (-2;-9)

Bài 3: Hệ phương trình $\left\{\begin{array}{l}x+2y=1\\ 2x-ay=3\end{array}\right.$ vô nghiệm khi a bằng bao nhiêu?

A. a=4                             

B. a= -6                                  

C. a=6                                    

D. a= -4

Bài 4: Giả sử x₁, x₂ là hai nghiệm của phương trình 2x² + 3x – 10 = 0 khi đó tích x₁. x₂ bằng:

A.$\frac{3}{2}$

B. $\frac{-3}{2}$                                     

C. -5                                       

D. 5

Bài 5: Trong hình vẽ bên:

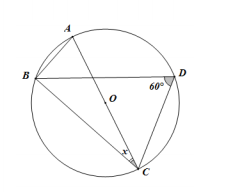
Biết AC là đường kính của đường tròn tâm O, góc BDC bằng 60^o và góc ACB bằng x. Khi đó x bằng:

A. 40^o                              

B. 45^o                                     

C. 35^o                                     

D. 30^o

Bài 6: Hai tiếp tuyến tại A và B của đường tròn (O;R) cắt nhau tại M, nếu $MA=R\sqrt{3}$ thì số đo góc ở tâm AOB bằng:

A. 120^o                            

B. 90^o                                     

C. 60^o                                     

D. 45^o

Bài 7: Cho hai đường tròn (O;R) và (O’;r) có bán kính lần lượt là R = 5 cm, r = 3cm và khoảng cách giữa hai tâm là 7cm. Khi đó:

A. (O) và (O’) tiếp xúc ngoài                                         

B. (O) và (O’) tiếp xúc trong

C. (O) và (O’) không giao nhau

D. (O) và (O’) cắt nhau

Bài 8: Cho hình trụ có bán kính đáy bằng 4cm, chiều cao bằng 5cm. Thể tích hình trụ bằng

A. 100π(cm³)                  

B. 80π(cm³)                           

C. 60π(cm³)                                   

D. 80(cm³)

II. Phần 2. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm)

1. Rút gọn các biểu thức sau:

1. Giải hệ phương trình

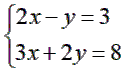
2. Xác định hệ số a và b của đường thẳng (d): y = ax + b, biết đường thẳng (d) song song với đường thẳng (d’): y = x + 2017 và đi qua điểm A(–1;2015)

Bài 2. (2,0 điểm)

1. Cho phương trình: x² – mx – 4 = 0 (1) ( với m là tham số)

a) Giải phương trình (1) khi m = 3

b) Tìm các giá trị của m để phương trình (1) có hai nghiệm x₁, x₂ thỏa mãn

2. Cho tam giác vuông có cạnh huyền bằng 20cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4cm. Tính độ dài mỗi cạnh góc vuông của tam giác vuông đó

Bài 3. (3,0 điểm)

Cho ∆ ABC có ba góc nhọn nội tiếp đường tròn (O). Kẻ AH ⊥ BC tại H. Gọi I và K lần lượt là hình chiếu vuông góc của A lên các tiếp tuyến tại B và C của đường tròn (O).

a) Chứng minh tứ giác AHCK nội tiếp đường tròn.

b) Chứng minh góc AHK = góc ABC và AH² = AI.AK

c) Gọi M, N theo thứ tự là trung điểm của AI và AK. Chứng minh rằng: Nếu AH = AM + AN thì ba điểm A, O, H thẳng hàng.

Bài 4 (1,0 điểm)

a) Cho a > 0, b > 0, c > 0. Chứng minh rằng: $(\mathrm{a}+\mathrm{b}+\mathrm{c})\left(\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{1}{\mathrm{c}}\right)\ge 9$

b) Cho 3 số thực dương a, b, c thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức: $\mathrm{P}=\frac{9}{2(\mathrm{ab}+\mathrm{bc}+\mathrm{ca})}+\frac{2}{{\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2}$

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TP HẢI PHÒNG NĂM 2016-2017

I.Phần 1. Trắc nghiệm (2,0 điểm)

1.A

2.B

3.D

4.C

5.D

6.A

7.D

8.B

II. Phần 2. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm)

1. Rút gọn các biểu thức sau:

a)

$$\begin{gathered} A=(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}):\sqrt{3} \\ =(2\sqrt{3}-5.3\sqrt{3}+4.2\sqrt{3}):\sqrt{3} \\ =-5\sqrt{3}:\sqrt{3} \\ =-5 \end{gathered}$$

b) 

$$\begin{gathered} B=\frac{2}{\sqrt{7}-\sqrt{6}}-\sqrt{28}+\sqrt{54} \\ =\frac{2(\sqrt{7}+\sqrt{6})}{(\sqrt{7}-\sqrt{6})(\sqrt{7}+\sqrt{6})}-\sqrt{7.4}+\sqrt{9.6} \\ =\frac{2\sqrt{7}+2\sqrt{6}}{7-6}-2\sqrt{7}+3\sqrt{6} \\ =2\sqrt{7}+2\sqrt{6}-2\sqrt{7}+3\sqrt{6} \\ =5\sqrt{6} \end{gathered}$$

2. Giải hệ phương trình

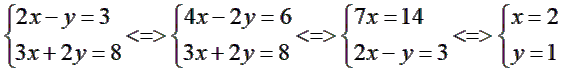
Vậy hệ phương trình có nghiệm duy nhất (2;1)

3. Đường thẳng (d): y = ax + b song song với đường thẳng (d’): y = x + 2017 nên ta có a = 1 và b ≠ 2017.

Khi đó (d) trở thành: y = x + b (b ≠ 2017)

Do đường thẳng (d) đi qua điểm A(-1;2015) nên ta có: 2015 = –1 + b

⇒ b = 2016 (thỏa mãn điều kiện)

Vậy phương trình đường thẳng (d) cần tìm là: y = x + 2016.

Bài 2. (2,0 điểm)

1.

a) Khi m = 3 thì phương trình (1) trở thành: x²-3x-4=0

Ta có: a - b + c = 1 – (-3) + (-4) = 0

Nên phương trình có 2 nghiệm phân biệt x = -1; x = 4

Vậy khi m = 3 thì phương trình có tập nghiệm là S = {-1;4}

b)Phương trình (1) có 2 nghiệm x₁; x₂ khi và chỉ khi

=>"m thì phương trình (1) luôn có 2 nghiệm x₁; x₂.

Áp dụng định lý Viet cho phương trình (1) ta có:

 

Theo bài ra ta có:

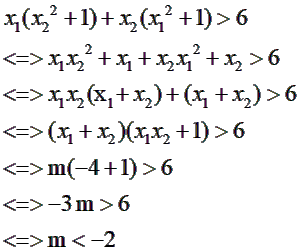
Vậy m < - 2 thỏa mãn yêu cầu bài toán.

2. Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm)

(x > 0)

Cạnh góc vuông lớn hơn của tam giác vuông đó dài là x + 4 (cm)

Theo Pitago, cạnh huyền của tam giác vuông đó dài là $\sqrt{x^2+{(x+4)}^2}$ (cm)

Vì cạnh huyền bằng 20cm nên $\sqrt{x^2+{(x+4)}^2}$ =20

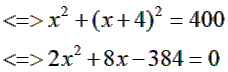
<=>x = 12 (tm) hoặc x = –16 (loại)

Vậy độ dài 2 cạnh góc vuông của tam giác vuông đó lần lượt là 12cm và

12 + 4 = 16cm.

Bài 3

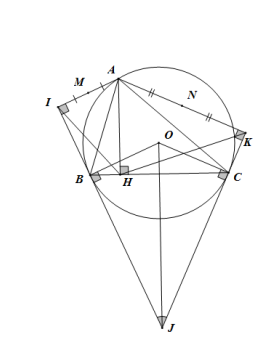
a) Vì AH ⊥ HC, AK ⊥ KC nên góc AHC = góc AKC = 90^o ⇒ góc AHC + góc AKC = 180^o

Suy ra AHCK là tứ giác nội tiếp$\frac{AI}{AH}=\frac{AH}{AK} => A{H}^2=AI.AK$

b) Vì AHCK là tứ giác nội tiếp nên góc AHK = góc ACK (2 góc nội tiếp cùng chắn cung AK)

Mặt khác góc ABC = góc ACK (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC của (O))

Suy ra góc AHK = góc ABC. (1)

Vì góc AHB = góc AIB = 90^o + 90^o = 180^o  nên AHBI là tứ giác nội tiếp ⇒ góc ABH = góc AIH hay góc ABC = góc AIH (2)

Từ (1) và (2) ⇒ góc AHK = góc AIH (3)

Chứng minh tương tự, ta có góc AHI = góc AKH (4)

Từ (3) và (4) có tam giác AIH đồng dạng với tam giác AHK(g-g)

$\frac{AI}{AH}=\frac{AH}{AK}\Rightarrow A{H}^2=AI.AK$ (đpcm)

c) Vì M, N là trung điểm của AI, AK nên

Kết hợp với ý b, ta có

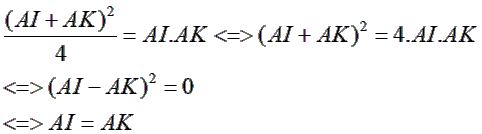
Gọi J là giao điểm của 2 tiếp tuyến tại B, C của (O). Có ∆ OBJ = ∆ OCJ (cạnh huyền cạnh góc vuông) ⇒ JO là phân giác của góc BJC và JB = JC

Suy ra OJ là đường trung trực của BC ⇒ OJ ⊥ BC

Vì AI = AK, AI ⊥ IJ, AK ⊥ KJ nên A thuộc đường phân giác của góc IJK ⇒ A ∈ OJ

Suy ra AO ⊥ BC, mà AH ⊥ BC nên A, O, H thẳng hàng.

Bài 4

a) Áp dụng bất đẳng thức Côsi cho ba số dương, ta có:

$\mathrm{a}+\mathrm{b}+\mathrm{c}\ge 3\sqrt[3]{\mathrm{abc}}$

$\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{1}{\mathrm{c}}\ge 3\sqrt[3]{\frac{1}{\mathrm{a}}.\frac{1}{\mathrm{b}}.\frac{1}{\mathrm{c}}}$

Nhân từng vế của hai bất đẳng thức cùng chiều dương, ta được:

 

$(\mathrm{a}+\mathrm{b}+\mathrm{c})\left(\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{\mathrm{q}}{\mathrm{c}}\right)⩾3\sqrt[3]{\frac{1}{\mathrm{a}}.\frac{1}{\mathrm{b}}.\frac{1}{\mathrm{c}}}=9$ (đpcm)

b) Với mọi a, b, c > 0 ta có

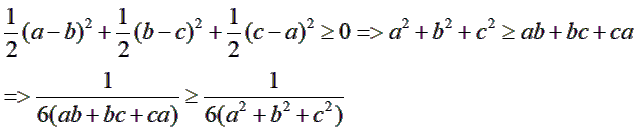
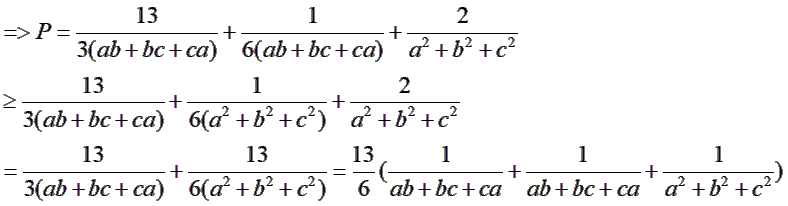
Áp dụng ý a, ta có

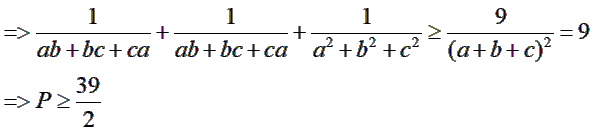
Dấu bằng xảy ra khi và chỉ khi $a=b=c=\frac{1}{3}$

Vậy GTNN của P là $\frac{39}{2}$

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2015 - 2016

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán TP Hải Phòng có đáp án - năm 2015

Phần I. Trắc nghiệm khách quan (2, 0 điểm)

Hãy chỉ chọn một chữ cái đứng trước câu trả lời đúng.

Bài 1. Biểu thức $M=\frac{1}{\sqrt{3x-1}}$ xác định khi cà chỉ khi:

A. $x\le \frac{1}{3}$                         

B. $x\ge \frac{1}{3}$                                   

C. $x>\frac{1}{3}$                                   

D. $x<\frac{1}{3}$

Bài 2. Hàm số nào sau đây nghịch biến trên R?

A. $y=\frac{x}{3}-1$                   

B. $y=\sqrt{2}x-3x$                     

C. $y=(\sqrt{5}-1)x$             

D. $y=(\sqrt{2}-1)x+\sqrt{2}$

Bài 3. Đường thẳng đi qua điểm M(1; -2) và song song với đường thẳng x – 2y = -3 có phương trình là:

A. $y=\frac{1}{2}x+\frac{5}{2}$                

B. $\frac{1}{2}x-\frac{5}{2}$                              

C. $\frac{1}{2}x+\frac{3}{2}$                                     

D. $\frac{1}{2}x-\frac{3}{2}$

Bài 4. Phương trình 3x² – 5x – 2015 có tổng hai nghiệm là:

A. $\frac{5}{6}$                                

B. $\frac{-5}{3}$                                     

C. $\frac{2015}{3}$                                   

D. $\frac{5}{3}$

Bài 5. Cho ∆MNP vuông tại M, đường cao MH (hình 1). Biết NH = 5 cm, HP = 9 cm.

Độ dài MH bằng:

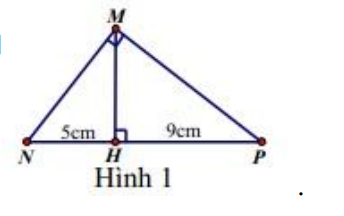
A. $3\sqrt{5}$cm                      

B. 7cm                                   

C. 4cm                                    

D. 4,5cm

Bài 6. Cho đường tròn (O; 25 cm) và dây AB = 40 cm. Khi đó khoảng cách từ tâm O

đến dây AB là:

A. 15cm                          

B. 7cm                                   

C. 20cm                                   

D. 24cm

Bài 7. Cho tam giác ABC nội tiếp đường tròn tâm O (hình 2), biết sđ cung AmB =

60⁰, sđ cung AnC = 140⁰ . Số đo của góc BAC bằng:

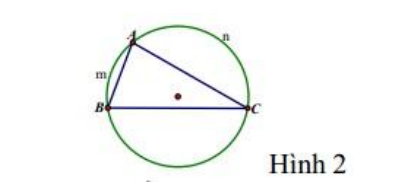
A. 40^o                              

B. 160^o                                   

C. 80^o                                     

D. 120^o

Bài 8. Khối nón có chiều cao bằng 12 cm, đường sinh bằng 15 cm thì có thể tích là:

A. 36π cm³                      

B. 81π cm³                             

C. 162π cm³                                   

D. 324π cm³

Phần II. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm)

1. Rút gọn các biểu thức sau:

a) $A=\sqrt{125}-4\sqrt{45}+3\sqrt{20}-\sqrt{80}$

b) $B=(3\sqrt{2}+\sqrt{6})\sqrt{6-3\sqrt{3}}$

2. Giải hệ phương trình, bất phương trình sau:

a)  $\left\{\begin{array}{l}3x+y=8\\ 7x-2y=23\end{array}\right.$   

b)  $\frac{x+3}{4}+1<x+\frac{x+2}{3}$  

Bài 2. (2,0 điểm)

1. Trong hệ trục Oxy, cho đường thẳng (d): y = (5m – 1)x – 6m² + 2m (m là tham số) và parabol (P): y = x² .

a) Tìm giá trị của m để (d) và (P) cắt nhau tại hai điểm phân biệt A và B.

b) Gọi x₁; x₂ lần lượt là hoành độ của A, B. Tìm giá trị của m để ${x_1}^2+{x_2}^2=1$

2. Một lâm trường dự định trồng 75 ha rừng trong một số tuần (mỗi tuần trồng được diện tích bằng nhau). Thực tế, mỗi tuần lâm trường trồng vượt mức 5 ha so với dự định nên cuối cùng đã trồng được 80 ha và hoàn thành sớm hơn dự định một tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu ha rừng?

Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A và AC > AB, D là một điểm trên cạnh AC sao cho CD < AD. Vẽ đường tròn tâm D và tiếp xúc với BC tại E. Từ B vẽ đường thẳng tiếp xúc với đường tròn (D) tại F (F khác E).

a) Chứng minh rằng năm điểm A, B, E, D, F cùng thuộc một đường tròn.

b) Gọi M là trung điểm của BC. Đường thẳng BF lần lượt cắt AM, AE, AD theo thứ tự tại các điểm N, K, I. Chứng minh: $\frac{IK}{I\text{F}}=\frac{AK}{\text{AF}}$ . Suy ra: IF.BK = IK . BF

c) Chứng minh rằng: tam giác ANF là tam giác cân.

Bài 4. (1,0 điểm)

a) Cho a, b > 0. Chứng minh rằng: 3(b² + 2a²) ≥ (b + 2a)²

b) Cho a, b, c > 0 thỏa mãn $\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\ge \frac{1}{2}$.Chứng minh rằng: $\frac{\sqrt{b^2+2a^2}}{ab}+\frac{\sqrt{c^2+2b^2}}{bc}+\frac{\sqrt{a^2+2c^2}}{ca}\ge \sqrt{3}$

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TP HẢI PHÒNG NĂM 2015-2016

I. Phần 1: Trắc nghiệm khách quan (2,0 điểm). Mỗi câu đúng được 0,25 điểm

Câu	1	2	3	4	5	6	7	8
Đáp án	C	B	B	D	A	A	C	D

II. Phần 2. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm)

a) $A=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}=-5\sqrt{5}$

b)$\begin{array}{l}B=(3\sqrt{2}+\sqrt{6})\sqrt{6-3\sqrt{3}}=(3+\sqrt{3})\sqrt{12-6\sqrt{3}}\\ =(3+\sqrt{3})|3-\sqrt{3}|=(3+\sqrt{3})(3-\sqrt{3})=9-3=6\end{array}$

2. 

$$\begin{gathered} a) \left\{\begin{array}{l}3x+y=8\\ 7x-2y=23\end{array}\right. \\ <=>\left\{\begin{array}{l}6x+2y=16\\ 7x-2y=23\end{array}\right. \\ <=>\left\{\begin{array}{l}13x=39\\ 3x+y=8\end{array}\right. \\ <=>\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right. \end{gathered}$$

Vậy hệ phương trình có nghiệm duy nhất (x, y) = (3; -1)

b)

 $$\begin{gathered} \frac{x+3}{4}+1<x+\frac{x+2}{3} \\ \iff 3x+9+12<12x+4x+8 \\ \iff -13x<-13 \\ \iff x>1 \end{gathered}$$

Vậy bất phương trình có nghiệm x > 1.

Bài 2. (2,0 điểm)

1. a) Xét phương trình hoành độ giao điểm của (d) và (P)$\begin{array}{l}{x}^2=(5m-1)x-6m^2+2m\\ <=>x^2-(5m-1)x+6m^2-2m=0\\ \Delta ={(m-1)}^2\end{array}$

Để (d) và (P) cắt nhau tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt <=> ∆ > 0  <=>  m ≠ 1.

b) (d) cắt (P) tại hai điểm phân biệt khi m ≠ 1.

hệ thức Vi-ét với phương trình (1) có $\left\{\begin{array}{l}{x}_1+x_2=5m-1\\ x_1{x}_2=6m^2-2m\end{array}\right.$

Lại có:

$\begin{array}{l}{x_1}^2+{x_2}^2=1\\ \iff {(x_1+x_2)}^2-2x_1{x}_2=1\\ \iff (5m^2-1)-2(6m^2-2m)=1\\ <=>13m^2-6m=0\\ <=>\left[\begin{array}{l}m=0\left(TM\right)\\ m=\frac{6}{13}\left(TM\right)\end{array}\right.\end{array}$

Vậy với m = 0;m= $\frac{6}{13}$ thì (d) cắt (P) tại hai điểm phân biệt thỏa mãn đầu bài.

2. Gọi diện tích rừng mà mỗi tuần lâm trường dự định trồng là x (ha). (Điều kiện: x > 0)

Theo dự định, thời gian trồng hết 75 ha rừng là: $\frac{75}{x}$(tuần)

Vì mỗi tuần lâm trường trồng vượt mức 5 ha so với dự định nên thực tế mỗi tuần lâm trường trồng được x + 5 (ha)

Do đó thời gian thực tế lâm trường trồng hết 80 ha rừng là $\frac{80}{x+5}$(tuần)

Vì thực tế, lâm trường trồng xong sớm so với dự định là 1 tuần nên ta có phương trình: $\frac{75}{x}-\frac{80}{x+5}=1$

Giải ra ta được: x = 15 (thỏa mãn điều kiện); x = -20 (loại)

Vậy mỗi tuần lâm trường dự định trồng 15 ha rừng.

Bài 3. (3,0 điểm)

Vẽ hình đúng cho phần a)

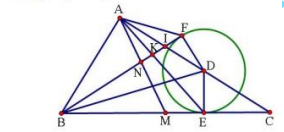
a) Theo tính chất tiếp tuyến, ta có:  $\widehat{BED}=\widehat{BFD}={90}^o$

Mà $\widehat{BAD}=\widehat{BAC}={90}^o$(giả thiết)

Do đó: $\widehat{BED}=\widehat{BFD}=\widehat{BAD}={90}^o$

Vậy: Năm điểm A, B, E, D, F cùng thuộc đường tròn đường kính BD.

b) Gọi (O) là đường tròn đường kính BD.

Trong đường tròn (O), ta có:

Cung DE = cung DF (do DE, DF là bán kính đường tròn (D))

=> $\widehat{EAD}=\widehat{DA\text{F}}$

Suy ra: AD là tia phân giác ̂ hay AI là tia phân giác của ∆KAF

Theo tính chất phân giác ta có $\frac{IK}{I\text{F}}=\frac{AK}{A\text{F}}$(1)

Vì AB ⊥ AI nên AB là tia phân giác ngoài tại đỉnh A của ∆KAF.

Theo tính chất phân giác ta có: $\frac{BK}{BF}=\frac{AK}{A\text{F}}$(2)

Từ (1) và (2) suy ra: $\frac{IK}{IF}=\frac{BK}{\text{BF}}$

Vậy IF . BK = IK. BF (đpcm)

c) Ta có: AM là trung tuyến thuộc cạnh huyền BC nên AM = MC,

Do đó ∆AMC cân tại M, suy ra: $\widehat{MCA}=\widehat{MAC}$

Từ đó $\widehat{NA\text{F}}=\widehat{MAC}+\widehat{DA\text{F}}=\widehat{MCA}+\widehat{EAC}$ (vì AI là tia phân giác của góc EAF)

Mà $\widehat{AEB}=\widehat{MCA}+\widehat{EAC}$ (góc ngoài của tam giác AEC)

Nên $\widehat{NA\text{F}}=\widehat{AEB}$

Mặt khác $\widehat{A\text{FB}}=\widehat{AEB}$ (góc nội tiếp cùng chắn cung AB)

=> $\widehat{\text{NAF}}=\widehat{BFA}=\widehat{NFA}$

Vậy: ∆ANF cân tại N (đpcm)

Bài 4. (1,0 điểm)

a) Ta có: 3(b² + 2a²) ≥ (b + 2a)²

<=> 3b² + 6a² ≥ b² + 4ab + 4a²

<=> 2(a – b)² ≥ 0 ∀a; b

Dấu “ ” xảy ra khi và chỉ khi a = b

b) Theo câu a

$\begin{array}{l}3(b^2+2a^2)\ge {(b+2a)}^2 <=>\sqrt{b}\end{array}$²+2a²≥b+2a3=>b2+2a2ab≥bc+2ac3abc(1)

Chứng minh tương tự:

$\begin{array}{l}\frac{\sqrt{c^2+2b^2}}{bc}\ge \frac{ca+2ab}{\sqrt{3}abc}\left(2\right)\\ \frac{\sqrt{a^2+2c^2}}{ca}\ge \frac{ab+2bc}{\sqrt{3}abc}\left(3\right)\end{array}$

Cộng (1), (2) và (3) vế với vế ta được

 $\frac{\sqrt{b^2+2a^2}}{ab}+\frac{\sqrt{c^2+2b^2}}{bc}+\frac{\sqrt{a^2+2c^2}}{ca}\ge \frac{3(ab+bc+ca)}{\sqrt{3}abc}=\sqrt{3}(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})\left(4\right)$

Áp dụng BĐT $\frac{1}{x}+\frac{1}{y}\ge \frac{4}{x+y}$ với x,y>0 ta có:

$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2}(\frac{2}{a}+\frac{2}{b}+\frac{2}{c})\ge \frac{1}{2}(\frac{4}{a+b}+\frac{4}{b+c}+\frac{4}{c+a})=2(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a})\ge 1$(5)

Từ (4) và (5) suy ra $\frac{\sqrt{b^2+2a^2}}{ab}+\frac{\sqrt{c^2+2b^2}}{bc}+\frac{\sqrt{a^2+2c^2}}{ca}\ge \sqrt{3}$

Dấu “=” xảy ra khi a = b = c = 3.