TOP 195 đề thi vào 10 môn Toán các tỉnh miền Bắc (2023) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

TOP 195 đề thi vào 10 môn Toán các tỉnh miền Bắc (2023) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Quảng Ninh

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Thái Nguyên

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Hà Nam

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Nam Định

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Vĩnh Phúc

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Hưng Yên

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Lào Cai

Bài 1: (2,5 điểm)

1. Thực hiện phép tính:

$\begin{array}{l}a)\sqrt{3}.\sqrt{12}\\ b)3\sqrt{20}+\sqrt{45}-2\sqrt{80}\end{array}$

2. Cho biểu thức: $P=(\frac{1}{\sqrt{a}-1}-\frac{1}{\sqrt{a}}):(\frac{\sqrt{a}+1}{\sqrt{a}-2}-\frac{\sqrt{a}+2}{\sqrt{a}-1})$ Với a>0;

a $\ne$1;a$\ne$4

a) Rút gọn P

b) So sánh giá trị của P với số $\frac{1}{3}$

Bài 2: (1,0 điểm) Cho hai hàm số bậc nhất y = -5x + (m+1) và y = 4x + (7 – m) (với

m là tham số). Với giá trị nào của m thì đồ thị hai hàm số trên cắt nhau tại một điểm

trên trục tung. Tìm tọa độ giao điểm đó.

Bài 3: (2,0 điểm) Cho hệ phương trình: $\left\{\begin{array}{l}(m-1)x+y=2\\ mx+y=m+1\end{array}\right.$ (m là tham số)

1) Giải hệ phương trình khi m = 2

2) Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất

(x; y) thỏa mãn: 2x + y £ 3

Bài 4: (1,5 điểm) Cho phương trình bậc hai x² + 4x - 2m + 1 = 0 (1) (với m là tham

số)

a) Giải phương trình (1) với m = -1.

b) Tìm m để phương trình (1) có hai nghiệm x₁ ; x₂ thỏa mãn điều kiện x₁-x₂=2.

Bài 5: (3,0 điểm)

Cho đường tròn tâm O bán kính R và một điểm A sao cho OA = 3R. Qua A kẻ 2 tiếp

tuyến AP và AQ với đường tròn (O ; R) (P, Q là 2 tiếp điểm). Lấy M thuộc đường tròn

(O ; R) sao cho PM song song với AQ. Gọi N là giao điểm thứ hai của đường thẳng

AM với đường tròn (O ; R). Tia PN cắt đường thẳng AQ tại K.

1) Chứng minh tứ giác APOQ là tứ giác nội tiếp và KA² = KN.KP

2) Kẻ đường kính QS của đường tròn (O ; R). Chứng minh NS là tia phân giác của góc PNM

3) Gọi G là giao điểm của 2 đường thẳng AO và PK. Tính độ dài đoạn thẳng AG theo bán kính R

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH LÀO CAI NĂM 2013-2014

Bài 1: (2,5 điểm)

1. Thực hiện phép tính:

$\begin{array}{l}a)\sqrt{3}.\sqrt{12}=\sqrt{36}=6\\ b)3\sqrt{20}+\sqrt{45}-2\sqrt{80}=6\sqrt{5}+3\sqrt{5}-8\sqrt{5}=\sqrt{5}\end{array}$

2. Cho biểu thức: $P=(\frac{1}{\sqrt{a}-1}-\frac{1}{\sqrt{a}}):(\frac{\sqrt{a}+1}{\sqrt{a}-2}-\frac{\sqrt{a}+2}{\sqrt{a}-1})$ Với a>0;

a $\ne$1;a$\ne$4

a) Rút gọn

$\begin{array}{l}P=(\frac{1}{\sqrt{a}-1}-\frac{1}{\sqrt{a}}):(\frac{\sqrt{a}+1}{\sqrt{a}-2}-\frac{\sqrt{a}+2}{\sqrt{a}-1})\\ =\frac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}(\sqrt{a}-1)}:\left(\frac{(\sqrt{a}+1)(\sqrt{a}-1)}{(\sqrt{a}-2)(\sqrt{a}-1)}-\frac{(\sqrt{a}+2)(\sqrt{a}-2)}{(\sqrt{a}-2)(\sqrt{a}-1)}\right)\\ =\frac{1}{\sqrt{a}(\sqrt{a}-1)}.\frac{(\sqrt{a}-2)(\sqrt{a}-1)}{(a-1)-(a-4)}=\frac{\sqrt{a}-2}{3\sqrt{a}}\end{array}$

b) So sánh giá trị của P với số $\frac{1}{3}$

Xét hiệu:

$\begin{array}{l}\frac{\sqrt{a}-2}{3\sqrt{a}}-\frac{1}{3}=\frac{\sqrt{a}-2-\sqrt{a}}{3\sqrt{a}}=\frac{-2}{3\sqrt{a}}<0\\ <=>P<\frac{1}{3}\end{array}$

Bài 2: (1,0 điểm) Đồ thị hai hàm số bậc nhất y = -5x + (m+1) và y = 4x + (7 – m) cắt

nhau tại một điểm trên trục tung khi tung độ góc bằng nhau tức là m+1 = 7 – m suy ra

m = 3. Tọa độ giao điểm đó là (0; m+1) hay (0; 7-m) tức là (0; 4)

Bài 3: (2,0 điểm) Cho hệ phương trình: $\left\{\begin{array}{l}(m-1)x+y=2\\ mx+y=m+1\end{array}\right.$ (m là tham số)

1) Giải hệ phương trình khi m = 2. Ta có $\left\{\begin{array}{l}x+y=2\\ 2x+y=3\end{array}\right.<=>\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$

2) y = 2 – (m-1)x thế vào phương trình còn lại ta có:

mx + 2 – (m-1)x = m + 1 $\iff$ x = m – 1 suy ra y = 2 – (m-1)² với mọi m

Vậy hệ phương trình luôn có nghiệm duy nhất (x; y) = (m-1; 2-(m-1)²)

2x + y = 2(m-1) + 2 – (m-1)² = -m² + 4m -1 = 3 – (m-2)² $\le$ 3 với mọi m

Vậy với mọi giá trị của m thì hệ phương trình luôn có nghiệm thỏa mãn: 2x + y$\le$3

Bài 4: (1,5 điểm) Cho phương trình bậc hai x² + 4x - 2m + 1 = 0 (1) (với m là tham

số)

a) Giải phương trình (1) với m = -1. Ta có x² + 4x +3 = 0 có a-b+c=1-4+3=0 nên x₁ =

-1 ; x₂ = -3

b) D ' = 3+2m để phương trình (1) có hai nghiệm x₁ ; x₂ thì $∆\text{'}\ge$0 tức là $m\ge -\frac{3}{2}$

Theo Vi ét ta có x₁+ x₂ = -4 (2); x₁.. x₂ = -2m+1 (3)

Kết hợp (2) vói đầu bài x₁-x₂=2 ta có hệ phương trình :

$\left\{\begin{array}{l}{x}_1+x_2=-4\\ x_1-x_2=2\end{array}\right.<=>\left\{\begin{array}{l}{x}_1=-1\\ x_2=-3\end{array}\right.$ thế vào (3) ta được m = -1 (thỏa mãn ĐK $m\ge \frac{-3}{2}$)

Vậy với m = -1 thì hệ phương trình (1) có hai nghiệm x₁ ; x₂ thỏa mãn điều kiện x₁

x₂=2

Bài 5: (3,0 điểm)

a) Tứ giác APOQ có tổng hai góc đối bằng 180⁰.

PM//AQ suy ra

$\widehat{PMN}=\widehat{KAN}$ (So le trong)

$\widehat{PMN}=\widehat{APK}$(cùng chắn cung PN)

=> $\widehat{KAN}=\widehat{APK}$

Tam giác KAN và tam giác KPA có góc K chung

$\widehat{KAN}=\widehat{KPA}$ nên hai tam giác đồng dạng (g-g)

$\frac{KA}{KP}=\frac{KN}{KA}=>K{A}^2=KN.KP$

b) PM//AQ mà SQ ^ AQ (t/c tiếp tuyến) nên SQ $\perp$ PM suy ra $\stackrel{⏜}{PS}=\stackrel{⏜}{SM}$

Nên $\widehat{PNS}=\widehat{SNM}$ hay NS là tia phân giác của góc $\widehat{PNM}$

c) Gọi H là giao điểm của PQ với AO

G là trọng tâm của tam giác APQ nên AG = 2/3 AH

Mà OP² = OA.OH nên OH = OP²/OA = R²/ 3R = R/3 nên AH = 3R – R/3 = 8R/3

do đó AG = 2/3 . 8R/3 = 16R/9

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tỉnh Hòa Bình

Bài 1: (3,0 điểm)

1) a) Tính giá trị biểu thức A = x² – 2x + 3 với x = 2.

b) Rút gọn: $B=\sqrt{20}-\sqrt{45}+2\sqrt{5}$

2)  Giải các phương trình sau

a) 2x + 1 = 3x – 5                                                          

b) $\frac{1}{x}-\frac{1}{2}=\frac{1}{2x}$

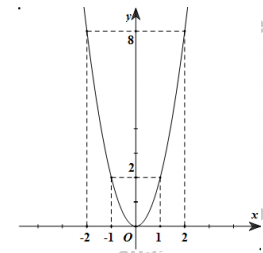
3) Cho hàm số y = 2x² có đồ thị là (P). Tìm trên (P) các điểm có tung độ bằng 4, vẽ đồ

thị (P).

Bài 2: (3,0 điểm)

1)    Giải phương trình: |2x – 5| + x = 3.

2)    Giải hệ phương trình: $\left\{\begin{array}{l}x+\frac{1}{y}=\frac{-1}{2}\\ 2x-\frac{3}{y}=\frac{-7}{2}\end{array}\right.$

3)    Cho phương trình: x² – 2(m + 1)x + m2 = 0 có hai nghiệm là x₁ và x₂ . Tìm m để

biểu thức $C={x_1}^2+{x_2}^2$ đạt giá trị nhỏ nhất

Bài 3: (1,0 điểm)

Năm học 2014 – 2015 hai trường A và B có tổng số 390 học sinh thi đỗ vào đại học đạt tỉ lệ 78%, biết trường A có tỉ lệ đỗ đại học là 75%, trường B có tỉ lệ đỗ đại học là 80%.

Tính số học sinh dự thi đại học năm học 2014 – 2015 ở mỗi trường.

Bài 4: (2,0 điểm)

Cho đường tròn tâm O, đường kính BC. Lấy một điểm A trên đường tròn (O) sao cho

AB > AC (A khác C). Từ A vẽ AH vuông góc với BC (H thuộc BC). Từ H vẽ HE

vuông góc với AB và HF vuông góc với AC (E thuộc AB, F thuộc AC)

1) Chứng minh rằng AEHF là hình chữ nhật và OA ⊥ EF

2) Tia FE cắt đường tròn (O) tại P. Chứng minh rằng ∆ APH cân

Bài 5: (1,0 điểm)

Cho các số thực a, b, c thỏa mãn $\left\{\begin{array}{l}a,b,c\in \text{[}0;2]\\ a+b+c=3\end{array}\right.$

Chứng minh rằng $a^2+b^2+c^2\le 5$

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH HÒA BÌNH NĂM 2015-2016

Bài 1:

1) a) Với x = 2 ta có A = 22 – 2.2 + 3 = 3

b) $B=\sqrt{2^2.5}-\sqrt{3^2.5}+2\sqrt{5}=2\sqrt{5}-3\sqrt{5}+2\sqrt{5}=\sqrt{5}$

2) a) 2x + 1 = 3x – 5 ⇔ 2x – 3x = –5 – 1 ⇔ –x = –6 ⇔ x = 6

Vậy tập nghiệm của phương trình đã cho là {6}

b) Điều kiện x ≠ 0

$\frac{1}{x}-\frac{1}{2}=\frac{1}{2x}<=>\frac{1}{x}-\frac{1}{2x}=\frac{1}{2}<=>(1-\frac{1}{2})\frac{1}{x}=\frac{1}{2}<=>\frac{1}{2}.\frac{1}{x}=\frac{1}{2}<=>\frac{1}{x}=1<=>x=1$

Vậy tập nghiệm của phương trình đã cho là {1}

2) Thay y = 4 ta có $4=2x^2<=>x^2=2<=>x=\pm \sqrt{2}$

Vậy các điểm cần tìm là $(\sqrt{2};4)$ và $(-\sqrt{2};4)$

Bảng giá trị

Đồ thị

Bài 2: 

1)    |2x-5|+x=3ó|2x-5|=3-x   (1)

Xét 2x-5$\ge$0 $\iff$$x\ge \frac{5}{2}$ thì |2x-5|=2x-5.

Phương trình (1) trở thành

2x-5=3-x $\iff$x=$\frac{8}{3}$ (thỏa mãn)

+Xét 2x-5<0 $\iff$ x<$\frac{5}{2}$ thì |2x-5|=5-2x.

Phương trình (1) trở thành

5-2x=3-x $\iff$ x=2(thỏa mãn)

Vậy tập nghiệm của phương trình đã cho là {2; $\frac{8}{3}$}

2) Điều kiện y ≠ 0. Đặt $\mathrm{t}=\frac{1}{\mathrm{y}}$, hệ phương trình đã cho trở thành

$$\begin{gathered} \left\{\begin{array}{l}x+t=\frac{-1}{2}\\ 2x-3t=\frac{-7}{2}\end{array}\right.<=>\left\{\begin{array}{l}t=\frac{-1}{2}-x\\ 2x-3(\frac{-1}{2}-x)=\frac{-7}{2}\end{array}\right.<=>\left\{\begin{array}{l}t=\frac{-1}{2}-x\\ 5x=-5\end{array}\right. \\ <=>\left\{\begin{array}{l}x=-1\\ t=\frac{1}{2}\end{array}\right.<=>\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right. \end{gathered}$$

(thỏa mãn)

Vậy hệ có nghiệm duy nhất là (–1;2)

3) Phương trình đã cho có hai nghiệm

$\begin{array}{l}<=>\Delta \text{'}={(m+1)}^2-(m^2-10)\ge 0\\ <=>2m+11\ge 0\\ <=>m\ge \frac{-11}{2}\end{array}$

Theo Vi–ét ta có x₁ + x₂ = 2(m + 1); x₁x₂ = m² – 10

Suy ra:

$\begin{array}{l}C={x_1}^2+{x_2}^2={(x_1+x_2)}^2-2x_1{x}_2=4-2(m^2-10)\\ =2m^2+8m+24=2{(m+2)}^2+16\ge 16\\ =>C\ge 16\end{array}$

Dấu bằng xảy ra khi và chỉ khi m = –2 (thỏa mãn)

Vậy giá trị nhỏ nhất của C là 16 khi m = –2

Bài 3:

Gọi số học sinh dự thi đại học ở trường A và trường B lần lượt là x và y (học sinh) (x,

y ∈ N*)

Tổng số học sinh 2 trường thi đỗ là 390 và tỉ lệ đỗ đại học của cả hai trường là 78% ⇒

Số học sinh dự thi đại học của cả hai trường là 390 : 78% = 500 (em)

Suy ra x + y = 500 (1)

Tỉ lệ đỗ đại học của trường A là 75% ⇒ Trường A có 0,75x học sinh đỗ đại học

Tỉ lệ đỗ đại học của trường B là 80% ⇒ Trường A có 0,8x học sinh đỗ đại học

Suy ra 0,75x + 0,8y = 390 (2)

Từ (1) và (2) giải hệ phương trình ta có x = 200; y = 300

Vậy số học sinh dự thi đại học ở trường A và trường B lần lượt là 200 và 300 học sinh.

Bài 4:

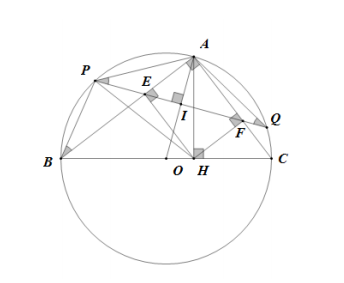
1) Có BAC = 90°  (góc nội tiếp chắn nửa đường tròn)

Vì HE ⊥ AB, HF ⊥ AC nên AEH=AFH = 90°

Tứ giác AEHF có 3 góc vuông nên nó là hình chữ nhật

Gọi I là giao OA và EF. Vì ∆ OAB cân ở O nên EAI=ABO  (1)

AEHF là hình chữ nhật nên nó nội tiếp đường tròn ⇒ AEI=AHF (2)

Vì AE // HF (cùng ⊥ AC) nên AHF=EAH=90^o- ABO (3)

Từ (1), (2), (3) ⇒ EAI+ AEI = 90° ⇒ ∆ AEI vuông tại I ⇒ OA ⊥ EF

2) Gọi Q là giao của tia EF với (O). Vì OA ⊥ PQ nên A là điểm chính giữa cung PQ

⇒ ∆ APQ cân tại A ⇒ APQ=AQP

Vì APBQ là tứ giác nội tiếp nên ABP=AQP

Suy ra ABP=APQ=APE=>tam giác ABP đồng dạng với tam giác APE (g-g)

$=>\frac{AB}{AP}=\frac{AP}{AE}=>A{P}^2=AE.AB$

Áp dụng hệ thức lượng trong tam giác vuông AHB có AH² = AE. AB

⇒ AP² = AH² ⇒ AP = AH ⇒ ∆ APH cân ở A.

Bài 5

Vì a,b,c ∈ [0;2] nên abc ≥ 0 và (2 – a)(2 – b)(2 – c) ≥ 0 ⇔ 8 + 2(ab + bc + ca) – 4(a +

b + c) – abc ≥ 0 ⇔ 2(ab + bc + ca) ≥ 4(a + b + c) + abc – 8

Mà a + b + c = 3; abc ≥ 0 nên 2(ab + bc + ca) ≥ 4 ⇒ ab + bc + ca ≥ 2

Suy ra a² + b² + c² = (a + b + c)2 – 2(ab + bc + ca) = 9 – 2(ab + bc + ca) ≤ 5

Dấu bằng xảy ra khi a = 0; b = 1; c = 2 và các hoán vị

Vậy a² + b² + c² ≤ 5

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2021 - 2022

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Bắc Giang - có đáp án (Tự luận) năm học 2015 - 2016

Bài 1: (2.0 điểm)

1. Tính giá trị của biểu thức $A=2(5\sqrt{16}-4\sqrt{25})+\sqrt{64}$

2. Biết đồ thị của hàm số $y=\frac{1}{3}a{x}^2$ , (a ≠ 0) đi qua điểm M(3; -6) hãy xác định giá trị của a.

Bài 2: (3.0 điểm)

1. Giải hệ phương trình $\left\{\begin{array}{l}2x-3y=1\\ 4x+y=9\end{array}\right.$ 

2. Rút gọn biểu thức $B=\left(\frac{1}{\sqrt{x}-2}-\frac{1}{\sqrt{x}+2}+\frac{4\sqrt{x}}{x-4}\right):\frac{\sqrt{x}+1}{x-4}$(với x ≥ 0; x ≠ 4).

3. Cho phương trình x² – (m² + 3)x + 2m² + 2 = 0 (x là ẩn, m là tham số) (1).

a) Giải phương trình (1) với m = -$\sqrt{3}$ 

b) Tìm m để phương trình (1) có hai nghiệm phân biệt lớn hơn 1.

Bài 3: (1,5 điểm) Nhà bạn Dũng được ông bà nội cho một mảnh đất hình chữ nhật.

Khi bạn Nam đến nhà bạn Dũng chơi, Dũng đố Nam tìm ra kích thước của mảnh đất

khi biết: mảnh đất có chiều dài gấp 4 lần chiều rộng và nếu giảm chiều rộng đi 2m,

tăng chiều dài lên gấp đôi thì diễn tích mảnh đất đó sẽ tăng thêm 20 m2. Các em hãy

giúp bạn Nam tìm ra chiều dài và chiều rộng của mảnh đất nhà bạn Dũng đó.

Bài 4: (3.0 điểm) Trên đường tròn (O) có đường kính AB = 2R, lấy một điểm C sao

cho AC = R và lấy điểm D bất kỳ trên cung nhỏ BC (điểm D không trùng với B và C).

Gọi E là giao điểm của AD và BC. Đường thẳng

đi qua điểm E và vuông góc với đường thẳng AB tại điểm H cắt tia AC tại điểm F.

Điểm M là trung điểm của

đoạn EF.

1. Chứng minh tứ giác BHCF là tứ giác nội tiếp.

2. Chứng minh: HA.HB = HE. HF

3. Chứng minh CM là tiếp tuyến của đường tròn (O).

4. Xác định vị trí của điểm D để chu vi của tứ giác ABDC lớn nhất.

Bài 5: (0,5 điểm) Cho ba số thực dương x, y, z thỏa mãn xy + xz + yz = 2016

Chứng minh rằng $\sqrt{\frac{yz}{x^2+2016}}+\sqrt{\frac{xy}{y^2+2016}}+\sqrt{\frac{xz}{z^2+2016}}\le \frac{3}{2}$ 

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH BẮC GIANG NĂM 2015-2016

Bài 1:

1. $A=2(5\sqrt{16}-4\sqrt{25})+\sqrt{64}$ $=2(5.4-4.5)+8=2(20-20)+8=8$

2. Đồ thị hàm số $y=\frac{1}{3}a{x}^2$, (a ≠ 0) đi qua điểm M(3; -6) khi – 6 =  $\frac{1}{3}a{.3}^2\iff -6=3a\iff a=-2$

Vậy a = -2 là giá trị cần tìm.

Bài 2:

1. $\left\{\begin{array}{l}2x-3y=1\\ 4x+y=9\end{array}\right.\iff \left\{\begin{array}{l}2x-3y=1\\ 12x+3y=27\end{array}\right.\iff \left\{\begin{array}{l}2x-3y=1\\ 14x=28\end{array}\right.\iff \left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$

Vậy hệ phương trình có nghiệm (x; y) = (2;1)

2. Ta có:

$$\begin{gathered} B=\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+2}+\frac{4\sqrt{x}}{x-4}\right):\frac{\sqrt{x}+1}{x-4} \\ =\frac{\sqrt{x}+2-\sqrt{x}+2+4\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{\sqrt{x}+1}=\frac{4(\sqrt{x}+1)}{x-4}.\frac{x-4}{\sqrt{x}+1}=4 \end{gathered}$$ 

Vậy B = 4, với x ≥ 0; x ≠ 4.

3. a. Với m =$-\sqrt{3}$ ta được phương trình x² – 6x + 8 = 0

Tính được ∆’ = 1

Kết luận được phương trình (1) có hai nghiệm x₁ = 2; x₂ = 4.

 b. Khẳng định được phương trình (1) có hai nghiệm phân biệt :

x₁ = 2; x₂ = m² + 1 khi m ≠ 1 và m ≠ -1

Để phương trình (1) có hai nghiệm phân biệt đều lớn hơn 1 thì m² + 1 > 1 ó m ≠ 0.

Kết luận: Với m ≠ -1; m ≠ 0 và m ≠ 1 thỏa mãn yêu cầu đầu bài.

Bài 3:

Gọi chiều rộng của mảnh đất là x (m) (điều kiện: x > 2)

Khi đó chiều dài của mảnh đất là: 4x (m)

Diện tích mảnh đất nhà bạn Dũng là: 4x² (m²)

Diện tích mảnh đất sau khi giảm chiều rộng 2m và tăng chiều dài lên gấp đôi là:

8x.(x – 2) (m²)

Theo bài ra ta có phương trình: 8x.(x – 2) – 4x² = 20

Giải phương trình ta được x = 5 và x = -1.

Đối chiếu với điều kiện ta được x = 5.

Vậy chiều rộng mảnh đất là 5m và chiều dài mảnh đất là 20m.

Bài 4:

1. Ta có: $\widehat{BHF}={90}^o$ (giả thiết)    (1).

$\widehat{BCA}={90}^o$ (góc nội tiếp chắn nửa đường tròn (O)).

Suy ra $\widehat{BCF}={90}^o$                        (2)

Từ (1) và (2) suy ra tứ giác BHCF nội tiếp một đường tròn (vì có hai đỉnh H, C kề nhau cùng nhìn BF dưới một góc vuông).

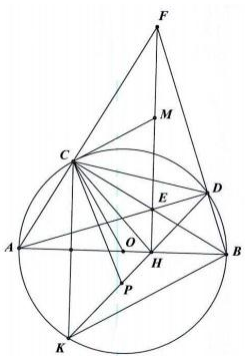
2. Xét tam giác vuông BHE và FHA có $\widehat{BEH}=\widehat{CAB}$ (cùng phụ với góc

$\widehat{CBA}$ ).

Suy ra hai tam giác BHE và FHA đồng dạng.

Từ đó ta có $\frac{HB}{HF}=\frac{HE}{HA}$ ó HA. HB = HE. HF

3. Tam giác vuông ECF vuông tại C có CM là đường trung tuyến nên CM = ME suy ra

CME là tam giác cân, suy ra $\widehat{MCE}=\widehat{MEC}$ (3)

$\widehat{MCO}=\widehat{MCE}+\widehat{ECO}=\widehat{MEC}+\widehat{CBO}$ (do (3) và tam giác COB cân tại O).

= $\widehat{BEH}+\widehat{CBO}={90}^o$ 

Vậy CM là tiếp tuyến của đường tròn (O).

4. Lấy điểm K đối xứng với điểm C qua AB. Suy ra điểm K cố định trên (O)

Lấy điểm P trên đoạn DK sao cho DP = DC.

Khẳng định tam giác OAC đều => tam giác CBK đều => tam giác CDP đều.

Xét hai tam giác CKP và CBD có:

CP = CD ; CK = CB và $\widehat{KCP}=\widehat{BCD}$ (cùng bằng 60^o - $\widehat{PCB}$ )

Từ đó, ∆CKP = ∆CBD (c.g.c) suy ra PK = BD.

Chu vi tứ giác ABDC bằng:

AB + BD + DC + CA = 3R + BD + DC = 3R + PK + PD = 3R + KD

Chu vi tứ giác lớn nhất khi KD lớn nhất => KD là đường kính của đường tròn (O; R).

Kết luận D là điểm chính giữa của cung nhỏ BC.

Bài 5:

Ta có: VT = $\sqrt{\frac{yz}{x^2+xy+xz+yz}}+\sqrt{\frac{xy}{y^2+xy+xz+yz}}+\sqrt{\frac{xz}{z^2+xy+xz+yz}}$ 

= $\sqrt{\frac{yz}{(x+y)(x+z)}}+\sqrt{\frac{xy}{(y+x)(y+z)}}+\sqrt{\frac{xz}{(z+x)(z+y)}}$

≤ $\frac{1}{2}\left(\frac{y}{x+y}+\frac{z}{x+z}\right)+\frac{1}{2}\left(\frac{x}{x+y}+\frac{y}{y+z}\right)+\frac{1}{2}\left(\frac{x}{x+z}+\frac{z}{y+z}\right)$ (theo BĐT Cô-si)

= $\frac{1}{2}\left(\frac{x}{x+y}+\frac{y}{x+y}\right)+\frac{1}{2}\left(\frac{x}{x+z}+\frac{z}{x+z}\right)+\frac{1}{2}\left(\frac{y}{y+z}+\frac{z}{y+z}\right)=\frac{3}{2}=VP$  

Đẳng thức xảy ra khi x = y = z = 4$\sqrt{42}$

.....................................................

.....................................................

.....................................................