TOP 195 đề thi vào 10 môn Toán các tỉnh miền Trung (2023) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

TOP 195 đề thi vào 10 môn Toán các tỉnh miền Trung (2023) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Thanh Hóa

Bài 1 (2,0 điểm)

1) Giải các phương trình sau:

a)    x – 5 = 0

b)    x² – 4x + 3 = 0

2)    Giải hệ phương trình: $\left\{\begin{array}{l}2x-y=1\\ 3x+y=4\end{array}\right.$

Bài 2 (2,0 điểm)

Cho biểu thức: 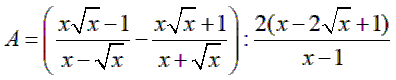   (với x > 0 và x ≠ 1)

1)    Rút gọn biểu thức A

2)    Tìm các số nguyên x để biểu thức A có giá trị nguyên.

Bài 3 (2,0 điểm)

Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx + 1 và parabol (P): y = 2x².

1)    Tìm m để đường thẳng (d) đi qua điểm A(1;3)

2)    Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt

A(x₁; y₁), B(x₂; y₂). Hãy tính giá trị của biểu thức T = x₁x₂ + x₂y₂

Bài 4 (3,0 điểm)

Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt

nhau tại E. Gọi F là điểm thuộc đường thẳng AD sao cho EF ⊥ AD. Đường thẳng CF

cắt đường tròn đường kính AD tại điểm thứ hai là M. Gọi N là giao điểm của BD và

CF. Chứng minh rằng:

1) Tứ giác CEFD nội tiếp đường tròn.

2) FA là đường phân giác của góc BFM.

3) BD.NE = BE.ND

Bài 5 (1,0 điểm)

Cho a, b, c là các số dương thỏa mãn: . Chứng minh rằng: 

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN THÀNH PHỐ THANH HÓA NĂM HỌC 2016-2017

Bài 1:

1)

a) x – 5 = 0 ⇔ x = 5. Vậy tập nghiệm của phương trình là {5}

b) x² – 4x + 3 = 0. Có a + b + c = 1 – 4 + 3 = 0 nên phương trình có hai nghiệm x = 1,

x = 3

Vậy tập nghiệm của phương trình là {1;3}

2)    $\left\{\begin{array}{l}2x-y=1\\ 3x+y=4\end{array}\iff \left\{\begin{array}{l}5x=5\\ 3x+y=4\end{array}\iff \left\{\begin{array}{l}x=1\\ 3.1+y=4\end{array}\iff \left\{\begin{array}{l}x=1\\ y=1\end{array}\right.\right.\right.\right.$

Hệ có nghiệm duy nhất (1;1)

Bài 2: 

1) Có

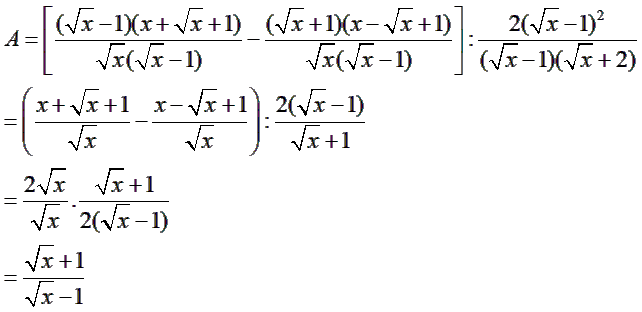
2)    

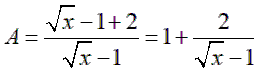
Vì x nguyên nên ta có A nguyên $\iff \frac{2}{\sqrt{x}-1}$ nguyên ó$\sqrt{x}-1$ là ước của 2

Mặt khác x > 0, x ≠ 1 nên $\sqrt{x}-1$> -1. Do đó:

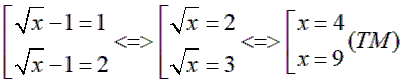
Vậy x = 4 hoặc x = 9 thỏa mãn đề bài.

Bài 3: 

1) Đường thẳng (d) đi qua điểm A(1;3) ⇔ 3 = m.1 + 1 ⇔ m = 2.

Vậy m = 2

2) Xét phương trình hoành độ giao điểm của (d) và (P):

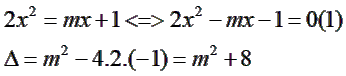
Vì 

Suy ra phương trình (1) luôn có 2 nghiệm phân biệt ∀ m ⇒ (d) luôn cắt (P) tại 2 điểm

phân biệt A(x₁; y₁), B(x₂; y₂) ∀ m trong đó x₁, x₂ là 2 nghiệm của (1) và 

Theo định lý Viét ta có: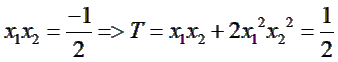 

Câu IV

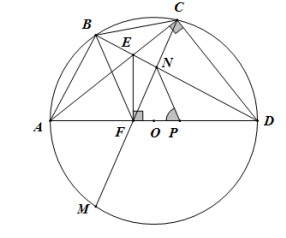
a) Có góc ACD = 90^o (góc nội tiếp chắn nửa đường tròn), hay góc ECD = 90^o

Mặt khác EF ⊥ AD nên góc EFD = 90^o

Suy ra góc ECD + góc EFD = 180^o ⇒ CEFD là tứ giác nội tiếp

b) Vì CEFD là tứ giác nội tiếp (cmt) nên góc CFD = góc CED (2 góc nội tiếp cùng

chắn cung CD)  (1)

Chứng minh tương tự có tứ giác ABEF nội tiếp ⇒ góc BFA = góc BEA (2 góc nội tiếp

cùng chắn cung BA) (2)

Có góc BEA = góc CED; góc AFM = góc CFD (đối đỉnh) (3)

Từ (1), (2), (3) ⇒ góc BFA = góc AFM ⇒ FA là phân giác góc BFM.

c) Vẽ NP // BF (P ∈ AD)

Ta có góc NPF = góc BFA (đồng vị) ; góc BFA = góc NFP ⇒ góc NPF = góc NFP ⇒ ∆

NFP cân ở N. ⇒ NP = NF

Vì NP // BF nên 

Vì góc BFA = góc NFP nên góc EFB = góc EFN (cùng phụ với 2 góc bằng nhau)

Suy ra FE là phân giác góc BFN của ∆ BFN. Theo định lý đường phân giác ta có $\frac{NP}{BF}=\frac{DN}{DB}\Rightarrow \frac{NF}{BF}=\frac{DN}{BD}$

Từ (4) và (5) $\Rightarrow \frac{DN}{DB}=\frac{NE}{BE}\Rightarrow BD.NE=BE.DN$(đpcm)

Bài 5:

Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số, ta có

Với mọi x,y,z > 0, áp dụng bất đẳng thức Côsi cho 3 số dương ta có

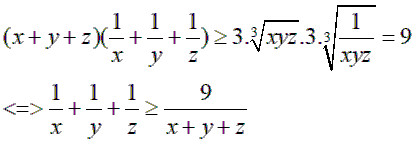
Áp dụng bất đẳng thức trên, ta có

$\frac{1}{a}+\frac{2}{b}=\frac{1}{a}+\frac{1}{b}+\frac{1}{b}\ge \frac{9}{a+b+b}\ge \frac{9}{3c}=\frac{3}{c}$(đpcm)

Dấu bằng xảy ra ⇔ a = b = c.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Nghệ An

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Quảng Ngãi

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Quảng Bình

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Quảng Trị

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Thừa Thiên Huế

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Khánh Hòa

Bài 1. ( 2 điểm)

Cho biểu thức $M=\frac{x\sqrt{y}-\sqrt{y}-y\sqrt{y}+\sqrt{x}}{1+\sqrt{xy}}$

1) Tìm điều kiện xác định và rút gọn M.

2) Tính giá trị của M, biết rằng $x={(1-\sqrt{3})}^2;y=3-\sqrt{8}$

Bài 2. (2 điểm)

1) Không dùng máy tính cầm tay, giải hệ phương trình: $\left\{\begin{array}{l}4\sqrt{x}-3\sqrt{y}=4\\ 2\sqrt{x}+\sqrt{y}=2\end{array}\right.$

2) Tìm giá trị của m để phương trình x² – mx + 1 = 0 có hai nghiệm phân biệt x₁, x₂

thoả mãn hệ thức ${(x_1+1)}^2+{(x_2+1)}^2=2$

Bài 3. ( 2,00 điểm)

Trong mặt phẳng toạ độ Oxy, cho parabol (P): y = - x²

1) Vẽ parabol (P).

2) Xác định toạ độ các giao điểm A, B của đường thẳng (d): y = -x – 2 và (P). Tìm toạ

điểm M trên (P) sao cho tam giác MAB cân tại M.

Bài 4. (4,00 điểm)

Cho tam giác ABC vuông tại A (AB<AC). Hai đường tròn (B; BA) và (C; CA) cắt

nhau tại điểm thứ hai là D. Vẽ đường thẳng a bất kì qua D cắt đường tròn (B) tại M và

cắt đường tròn (C) tại N ( D nằm giữa M và N). Tiếp tuyến tại M của đường tròn (B)

và tiếp tuyến tại N của đường tròn (C) cắt nhau tại E.

1) Chứng minh BC là tia phân giác của ABD

2) Gọi I là giao điểm của AD và BC. Chứng minh: AD² = 4BI.CI

3) Chứng minh bốn điểm A, M, E, N cùng thuộc một đường tròn.

4) Chứng minh rằng số đo MEN không phụ thuộc vị trí của đường thẳng a.

ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH KHÁNH HÒA NĂM HỌC 2015-2016

Bài 1:

a) ĐK: x³0; y³0

$\begin{array}{l}M=\frac{x\sqrt{y}-\sqrt{y}-y\sqrt{y}+\sqrt{x}}{1+\sqrt{xy}}=\frac{x\sqrt{y}-y\sqrt{x}+\sqrt{x}-\sqrt{y}}{1+\sqrt{xy}}\\ =\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})+(\sqrt{x}-\sqrt{y})}{1+\sqrt{xy}}=\frac{(\sqrt{x}-\sqrt{y})(1+\sqrt{xy})}{1+\sqrt{xy}}=\sqrt{x}-\sqrt{y}\end{array}$

b) Với $x={(1-\sqrt{3})}^2;y=3-\sqrt{8}$

$M=\sqrt{{(1-\sqrt{3})}^2}-\sqrt{{(\sqrt{2}-1)}^2}=\sqrt{3}-1-\sqrt{2}+1=\sqrt{3}-\sqrt{2}$

Bài 2:

a)

$\begin{array}{l}\left\{\begin{array}{l}4\sqrt{x}-3\sqrt{y}=4\\ 2\sqrt{x}+\sqrt{y}=2\end{array}\right.<=>\left\{\begin{array}{l}4\sqrt{x}-3\sqrt{y}=4\\ 4\sqrt{x}+2\sqrt{y}=4\end{array}\right.<=>\left\{\begin{array}{l}5\sqrt{y}=0\\ 2\sqrt{x}+\sqrt{y}=2\end{array}\right.\\ <=>\left\{\begin{array}{l}\sqrt{y}=0\\ 2\sqrt{x}=2\end{array}\right.<=>\left\{\begin{array}{l}y=0\\ x=1\end{array}\right.\end{array}$

b) $\Delta ={(-m)}^2-\mathrm{4.1.1}=m^2-4$

Để phương trình có hai nghiệm phân biệt thì: m² – 4 ³ 0 Û m³2 hoặc m£-2

Theo hệ thức Viet, ta có: x₁ + x₂ = m; x₁.x₂ = 1

Ta có:

$\begin{array}{l}{(x_1+1)}^2+{(x_2+1)}^2=2\\ <=>{x_1}^2+2x_1+1+{x_2}^2+2x_2+1=2\\ <=>{(x_1+x_2)}^2+2(x_1+x_2)-2x_1{x}_2=0\end{array}$

Suy ra: m² +2m-2=0ó $\left[\begin{array}{l}m=\sqrt{3}-1\left(L\right)\\ m=-\sqrt{3}-1\left(TM\right)\end{array}\right.$

Vậy m= $-\sqrt{3}-1$

Bài 3:

a) Vẽ đồ thị y = -x²

TXĐ: D = R

Tọa độ đỉnh: I(0;0)

Trục đối xứng: x = 0

Tính biến thiên:

Hàm số đồng biến trên (-∞;0) và nghịch biến trên (0;+∞).

BBT:

Bảng giá trị

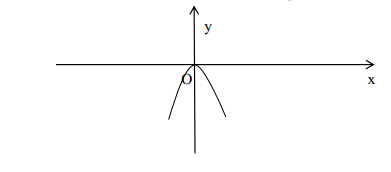
b) HD: Viết pt đường trung trực (d’) của AB, tìm giao điểm của (d’) và (P), ta tìm được

hai điểm M.

Hoành độ các giao điểm A, B của đường thẳng (d): y = -x – 2 và (P) là nghiệm của phương trình: – x² = – x – 2 Û x² – x – 2 =0 Û x= -1 hoặc x = 2

+ Với x = -1, thay vào (P), ta có: y = –(-1)² = -1, ta có: A(-1; -1)

+ Với x = 2, thay vào (P), ta có: y = –(2)² = -4, ta có: B(2; -4)

Suy ra trung điểm của AB là: $\mathrm{I}(\frac{1}{2};\frac{-5}{2})$

Đường thẳng (d’) vuông góc với (d) có dạng: y = x + b;

Vì (d’): y = x + b đi qua I nên: $\frac{-5}{2}=\frac{1}{2}+\mathrm{b}<=>\mathrm{b}=-3$

Vậy (d’): y = x -3

Phương trình hoành độ của (d’) và (P) là: x² + x - 3 = 0 $<=>x=\frac{-1\pm \sqrt{13}}{2}$

+ Với $x=\frac{-1-\sqrt{13}}{2}=>y=\frac{-7-\sqrt{13}}{2}$

+Với $x=\frac{-1+\sqrt{13}}{2}=>y=\frac{-7+\sqrt{13}}{2}$

Vậy có hai điểm M cần tìm là: $(\frac{-1-\sqrt{13}}{2};\frac{-7-\sqrt{13}}{2})$ và $(\frac{-1+\sqrt{13}}{2};\frac{-7+\sqrt{13}}{2})$

Bài 4:

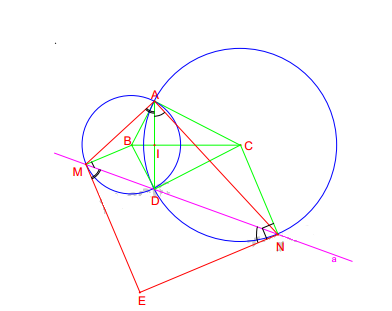
a) C/m: DABC = DDBC (ccc) Þ ABC=DBC  hay: BC là phân giác của ABD

b) Ta có: AB = BD (=bk(B))

CA = CD (=bk(C))

Suy ra: BC là trung trực của AD hay BC ^ AD ÞAI^B

Ta lại có: BC ^ AD tại I Þ IA = ID (đlí)

Xét DABC vuông tại A (gt) có: AI^BC, suy ra: AI² = BI.CI hay: 

$\frac{A{D}^2}{4}=BI.CI=>A{D}^2=4BI.CI$

c) Ta có: DME=DAM (hệ quả t/c góc tạo bởi tia tuyến và dây cung)

DNE =DAN (hệ quả t/c góc tạo bởi tia tuyến và dây cung)

Suy ra: DME+ DNE=DAM+DAN

Trong DMNE có: MEN+EMN+ENM = 180^o , suy ra: MEN+DAM+DAN = 180^o

Hay: MEN+MAN =180^o Þ tứ giác AMEN nội tiếp.

d) Trong DAMN có: MAN+AMN+ANM = 180^o , mà: MEN+MAN =180^o

suy ra: MEN=AMN+ANM

Ta lại có: $AND=ACB=\frac{1}{2}ACD,AMD=ABC=\frac{1}{2}ABD$ (góc ở tâm và góc nội tiếp cùng

chắn một cung)

Mà: DABC vuông tại A nên: MEN = 90^o (không đổi)

Vậy số đo góc MEN không phụ thuộc vào đường thẳng a.

.............................................

.............................................

.............................................