TOP 195 đề thi vào 10 môn Toán các tỉnh miền Nam (2023) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

TOP 23 đề thi vào 10 môn Toán các tỉnh miền Nam (2023) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Đồng Nai

Bài 1. (1,5 điểm)

1) Giải phương trình 5x² – 16x + 3 = 0

2) Giải hệ phương trình $\left\{\begin{array}{l}3x-2y=5\\ x+3y=7\end{array}\right.$

3) Giải phương trình x⁴ + 9x² = 0

Bài 2. (2,5 điểm)

1) Tính: $\frac{2}{\sqrt{2}+2}+\frac{1}{3}.\sqrt{18}$

2) Tìm m để đồ thị hàm số y = 4x + m đi qua điểm (1;6)

3)    Vẽ đồ thị (P) của hàm số $y=\frac{x^2}{2}$ . Tìm tọa độ giao điểm của (P) và đường thẳng

y = 2.

Bài 3. (1,25 điểm)

Hai công nhân cùng làm chung một công việc trong 6 giờ thì xong. Nếu người thứ nhất

làm trong 3 giờ 20 phút và người thứ hai làm trong 10 giờ thì xong công việc. Tính

thời gian mỗi công nhân khi làm riêng xong công việc.

Bài 4. (1,25 điểm)

1) Chứng minh phương trình x² – 2x – 2 = 0 có hai nghiệm phân biệt x₁, x₂. Tính T = 2x₁ + x₂.(2 – 3x₁).

2) Chứng minh x² – 3x + 5 > 0, với mọi số thực x.

Bài 5. (3,5 điểm)

Cho đường tròn (O) tâm O đường kính AB. Lấy hai điểm phân biệt C và D thuộc

đường tròn (O); biết C và D nằm khác phía đối với đường thẳng AB. Gọi E, F tương

ứng là trung điểm của hai dây AC, AD.

1) Chứng minh AC² + CB² = AD² + DB².

2) Chứng minh tứ giác AEOF nội tiếp đường tròn. Xác định tâm đường tròn ngoại tiếp

tứ giác AEOF.

3) Đường thẳng EF cắt đường tròn ngoại tiếp tam giác ADE tại điểm K khác E. Chứng

minh đường thẳng DK là tiếp tuyến của đường tròn (O). Tìm điều kiện của tam giác

ACD đề tứ giác AEDK là hình chữ nhật.

 ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH ĐỒNG NAI NĂM HỌC 2015-2016

Bài 1

1 .1 Giải pt 5x² - 16x + 3 = 0

D’ = (-8)² - 5.3 = 49

Phương trình có 2 nghiệm $x_{1,2}=\frac{-b\text{'}\pm \sqrt{\Delta \text{'}}}{a}=\frac{8\pm 7}{5}=>x_1=3;x_2=\frac{1}{2}$

Vậy phương trình đã cho có 2 nghiệm phân biệt.

1.2 Giải hệ$\left\{\begin{array}{l}3x-2y=5\\ x+3y=7\end{array}\right.<=>\left\{\begin{array}{l}3x-2y=5\\ 3x+9y=21\end{array}\right.<=>\left\{\begin{array}{l}3x-2y=5\\ 11y=16\end{array}\right.<=>\left\{\begin{array}{l}x=\frac{29}{11}\\ y=\frac{16}{11}\end{array}\right.$

Vậy hệ đã cho có 1 nghiệm duy nhất.

1.3 Giải pt x⁴ + 9x² = 0

$\iff$ x²(x² + 9) =0

$\left[\begin{array}{l}{x}^2=0\\ x^2+9=0\end{array}\right.<=>\left[\begin{array}{l}x=0\\ x^2=-9\left(VN\right)\end{array}\right.$

Vậy phương trình đã cho có 1 nghiệm duy nhất x = 0.

Bài 2

2.1 Tính

$\begin{array}{l}\frac{2}{\sqrt{2}+2}+\frac{1}{3}\sqrt{18}=\frac{\sqrt{2}}{1+\sqrt{2}}+\frac{\sqrt{9.2}}{3}=\frac{\sqrt{2}(\sqrt{2}-1)}{1-2}+\frac{3\sqrt{2}}{3}\\ =\frac{\sqrt{2}-2}{-1}+\sqrt{2}=2-\sqrt{2}+\sqrt{2}=2\end{array}$

2.2 Tìm m để đồ thi hàm số y = 4x + m đi qua (1;6)

Thay x = 1 ; y = 6 vào ta có 6 = 4.1 + m => m = 2

2.3 Vẽ đồ thị (P) của hàm số $y=\frac{x^2}{2}$. Tìm tọa độ giao điểm của (P) và đường thẳng

y = 2.

Bảng giá trị:

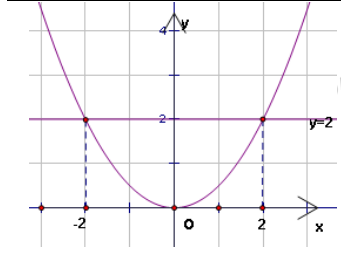
(P) cắt (d) y = 2 nên y = 2 thỏa (P)

$\begin{array}{l}=>2=\frac{x^2}{2}\\ =>\left[\begin{array}{l}{x}_1=2\\ x_2=-2\end{array}\right.\end{array}$

hay tọa đô giao điểm là ( (-2;2) và (2 ; 2)

Bài 3

Gọi x (h) là thời gian người thứ nhất làm 1 mình xong công việc ( x > 6) .

Thì trong 1h người thứ nhất làm được 1/x (cv)

y (h) là thời gian người thứ hai làm 1 mình xong công việc ( y > 6)

Trong 1h người thứ hai làm được 1/y (cv)

Trong 3h20' người thứ nhất làm được $\frac{10}{3}.\frac{1}{x}$(công việc) trong 10h người thứ hai làm

được $10.\frac{1}{y}$ (công việc)

Ta có hệ phương trình

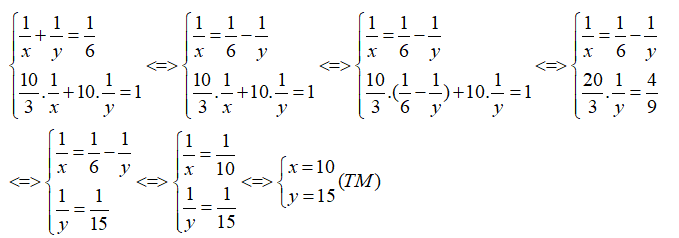
Bài 4 .

1) C/m pt x² - 2x -2 =0 luôn có 2 nghiệm phân biệt

$\Delta \text{'}={(-1)}^2-1(-2)=3>0$ nên pt luôn có 2 nghiệm phân biệt

Theo Viet ta có: x₁ + x₂ = 2 ; x₁ .x₂ = -2

Tính T = 2x₁ + x₂(2 - 3x₁) = 2(x₁ + x₂ )- 3x₁. x₂ =2.(2) -3.(-2)= 10

2) C/m x² - 3x + 5 > 0 với mọi x

$x^2-3x+5=x^2-2.x.\frac{3}{2}+{\left(\frac{3}{2}\right)}^2-{\left(\frac{3}{2}\right)}^2+5={(x-\frac{3}{2})}^2+\frac{11}{4}>0$

Bài 5.

Cách 1

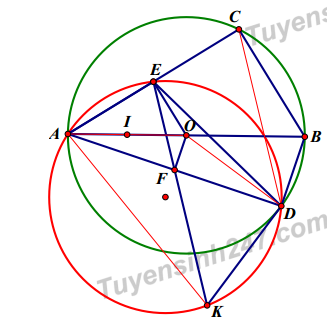
a) Dùng định lí Pytago cho tam giác vuông ACB và ADB

b) Ta có E là trung điểm của AC, F là trung điểm của AD nên OE vuông góc với AC,

OF vuông góc với AD do đó tứ giác AEOF có tổng hai góc đối là 2v nên nội tiếp. Do

góc AEO vuông nên tâm I đường tròn ngoại tiếp tứ giác AEOF là trung điểm của AO.

c) * Ta có tam giác OAD cân tại O nên góc OAD = góc ODA, mà góc ADK = góc

AEK = góc AOF. Do góc OAD + góc AOF = 90⁰ nên góc ODA + góc ADK = 90⁰ suy

ra DK vuông góc với DO suy ra KD là tiếp tuyến (O).

* Ta có OF là đường trung bình tam giác ABD nên OF // DB suy ra AOF = góc ABD =

góc ACD.

Để tứ giác AEDK là hình chữ nhật thì EF = FK = FA = FD suy ra góc FAE = góc FEA

suy ra góc FAE = góc ACD do đó tam giác ACD cân tại D

Cách 2

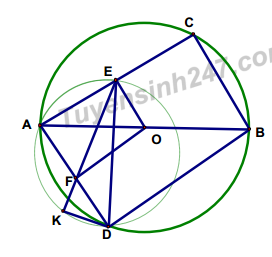
1) C/m AC² +CB² = AD² + DB²

D ABC vuông tại C . Theo Pitago thì AB² = AC² +CB²

D ABD vuông tại D . Theo Pitago thì AB² = AC² +CB²

Suy ra AC² +CB² = AD² + DB²

2) Cm AOEF nội tiếp

E là trung điểm dây AC nên OE ^ AC hay AEO=90^o

F là trung điểm dây AD nên OF ^ AD hay AFO=90^o

AEO+AFO =180^o =>AOEF nội tiếp (tổng 2 góc đối bằng 180⁰) ,. Tâm của đường tròn

là trung điểm OA

3) C/m DK là tiếp tuyến (O).

D ABD có FO là đường trung bình nên AOF =ABD

ADK =AEF (AEK)= AOF =ABD = $\frac{1}{2}sdAD$

Vậy DK là tiếp tuyến (O)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Cà Mau

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Bình Dương

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Tây Ninh

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - An Giang

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Bình Định

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán có đáp án - Bình Phước

Bài 1: (2,0 điểm)

1. Tính giá trị của các biểu thức sau:

$N=1+\sqrt{81}\text{ H=}\sqrt{{(3+\sqrt{5})}^2}+\sqrt{5}$

2. Cho biểu thức G = $\frac{x-\sqrt{x}}{\sqrt{x}-1}-\frac{x-1}{\sqrt{x}+1}$.Tìm x để G có nghĩa và rút gọn G.

Bài 2 (2,0 điểm)

1. Cho parabol (P): y = - x² và đường thẳng d: y = 3x +2

a.     Vẽ parabol (P) và đường thẳng d trên cùng một hệ trục toạ độ.

b.    Viết phương trình đường thẳng d’ vuông góc với đường thẳng d và tiếp xúc với

(P).

2. Không sử dụng máy tính, giải hệ phương trình: $\left\{\begin{array}{l}3x-y=5\\ 5x+2y=23\end{array}\right.$

Bài 3: (2,5 điểm)

1.    Cho phương trình x² + mx + 1 = 0 (1), m là tham số

a. Giải phương trình (1) khi m = 4

b.Tìm giá trị của m để phương trình (1) có hai nghiệm x1; x2 thoả mãn $\frac{x_1^2}{x_2^2}+\frac{x_2^2}{x_1^2}>7$

2. Cho mảnh vườn hình chữ nhật có diện tích 360 m2. Nếu tăng chiều rộng 2m và

giảm chiều dài 6m thì diện tích không thay đổi. Tính chu vi của mảnh vườn lúc

ban đầu.

Bài 4 : (1,0 điểm)

Cho tam giác ABC vuông tại A, có cạnh AB = 6cm, $\widehat{C}$ = 60⁰. Hãy tính các cạnh còn lại

và đường cao, đường trung tuyến hạ từ A của tam giác ABC.

Bài 5: (2,5 điểm)

Cho tam giác ABC nhọn nội tiếp đường tròn (O;R), các tiếp tuyến tại B và C với

đường tròn (O;R) cắt nhau tại E, AE cắt (O;R) tại D (khác điểm A).

1. Chứng minh tứ giác OBEC nội tiếp đường tròn .

2. Từ E kẻ đường thẳng d song song với tiếp tuyến tại A của (O;R), d cắt các đường

Thẳng AB, AC lần lượt tại P, Q. Chứng minh AB.AP = AD.AE

3. Gọi M là trung điểm của đoạn thẳng BC. Chứng minh EP = EQ và $\widehat{PAE}=\widehat{MAC}$

4.  Chứng minh AM.MD = $\frac{B{C}^2}{4}$

 ĐÁP ÁN ĐỀ THI VÀO 10 MÔN TOÁN TỈNH BÌNH PHƯỚC NĂM HỌC 2014-2015

Bài 1:

$\begin{array}{l}1:N=1+\sqrt{81}=1+9=10\\ H=\sqrt{{(3-\sqrt{5})}^2}+\sqrt{5}=|3-\sqrt{5}|+\sqrt{5}=3-\sqrt{5}+\sqrt{5}=3\end{array}$

2:Điều kiện $x\ge 0$ và $x\ne 1$

$G=\frac{x-\sqrt{x}}{\sqrt{x}-1}-\frac{x-1}{\sqrt{x}+1}=\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}-1}-\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}+1}=\sqrt{x}-(\sqrt{x}-1)=1$

Bài 2:

1.

a. + Bảng một số giá trị của (P):

+ (d) đi qua 2 điểm (0;2) và (-1;-1)

+ Đồ thị:

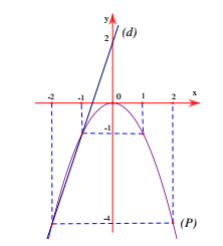
b. d’ có dạng : y = a’x + b’; d’$\perp d<=>a.a\text{'}=-1$

với a = 3 $=>a\text{'}=\frac{-1}{3}=>d\text{'}:y=\frac{-1}{3}x+b\text{'}$

Pt hoành độ giao điểm của (P) và d’: -x² = $\frac{-1}{3}x+b\text{'}<=>x^2-\frac{-1}{3}x+b\text{'}=0(*)$

PT (*) có $\Delta =\frac{1}{9}-4b\text{'}$

d tiếp xúc với (P) khi $\Delta =\frac{1}{9}-4b\text{'}$=0ó$b\text{'}=\frac{1}{36}$

Vậy d có pt: $y=\frac{-1}{3}x+\frac{1}{36}$

2:Hệ pt $\left\{\begin{array}{l}3x-y=5\\ 5x+2y=23\end{array}\right.$<=>$\left\{\begin{array}{l}6x-2y=10\\ 5x+2y=23\end{array}\right.<=>\left\{\begin{array}{l}11x=33\\ 3x-y=5\end{array}\right.<=>\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$

Vậy hệ pt có nghiệm x=3; y = 4

Bài 3:

1:

a. Khi m = 4 ta có pt: x2 + 4x + 1 = 0 (*)

Pt (*) có $\Delta =3>0$

=>x_1,2=$-2\pm \sqrt{3}$

Vậy khi m = 4 pt (1) có 2 nghiệm x_1,2=$-2\pm \sqrt{3}$

b: PT (1) có hai nghiệm x_1,2

$\begin{array}{l}\Delta =m^2-4\ge 0<=>m^2\ge 4<=>\left|m\right|\ge 2\\ <=>\left[\begin{array}{l}m\ge 2\\ m\le -2\end{array}\right.\end{array}$

Áp dụng định lý Viet cho pt (1): $\left\{\begin{array}{l}S=x_1+x_2=-m\\ P=x_1{x}_2=1\end{array}\right.$ .Theo đề bài:

2. Gọi x(m) là chiều rộng của mảnh vườn hình chữ nhật (x >0)

Chiều dài của mảnh vườn hình chữ nhật : $\frac{360}{x}$

Theo đề bài ta có pt: (x+2)($\frac{360}{x}$-6)=360

<=>-6x²-12x+720=0

<=>x²+2x-120=0

<=>$\left[\begin{array}{l}x=10\left(TM\right)\\ x=-12\left(L\right)\end{array}\right.$

Với x=10=> $\frac{360}{x}$=36.Chu vi của mảnh vườn : 2(10+36) = 92 (m²)

Bài 4 (1,0 điểm)

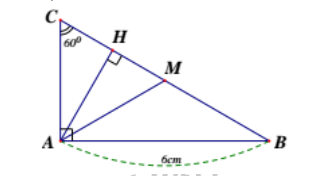
Tam giác ABC vuông tại A nên :

+ B + C = 90⁰ =>B = 30⁰

+ AC = AB.tanB = 6.tan30⁰ = 6.$\frac{\sqrt{3}}{3}=2\sqrt{3}\left(cm\right)$

$\begin{array}{l}+\mathrm{BC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AC}}^2}=\sqrt{6^2+{\left(2\sqrt{3}\right)}^2}=4\sqrt{3}\left(\mathrm{cm}\right)\\ +\mathrm{AB}.\mathrm{AC}=\mathrm{BH}.\mathrm{AH}=>\mathrm{AH}=\frac{\mathrm{AB}.\mathrm{AC}}{\mathrm{BC}}=\frac{6.2\sqrt{3}}{4\sqrt{3}}=3\left(\mathrm{cm}\right)\\ +\mathrm{AM}=\frac{1}{2}\mathrm{BC}=\frac{1}{2}4\sqrt{3}=2\sqrt{3}\left(\mathrm{cm}\right)\end{array}$

Bài 5:

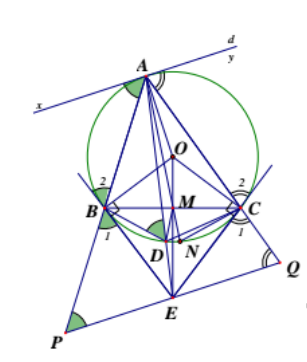
1. (O) có :

- BE là tiếp tuyến tại B=>BE$\perp$OB=>OBE=90^O nhìn đoạn OE (1)

- CE là tiếp tuyến tại C=> CE$\perp$OB=>OCE=90^O nhìn đoạn OE (2)

Từ (1), (2) tứ giác OBEC nội tiếp đường tròn đường kính OE

2. (O) có:

- ADB = BAx (cùng chắn cung AB) (1)

- PQ // d APE = Bax (so le trong) (2)

Từ (1),(2) góc ADB = APE

Tam giác ABD và tam giác AEP có: ADB = APE (cmt) và EAP chung=>tam giác ABD

đồng dạng với tam giác AEP (g.g)

=> $\frac{AB}{AE}=\frac{AD}{AP}=>AB.AP=AD.AE\left(DPCM\right)$

3. (O) có:

Góc BAx = B2 (cùng chắn AB)

Góc B1 = B2 (đối đỉnh)

=>góc BAx=B1

Mà góc BAx = APE (cmt) =>góc B1 = APE=>tam giác BEP cân tại E =>EB=EP(1)

(O) có: CAy = C2 (cùng chắn AC); C1 = C2 (đối nhau)

=>CAy = C1

PQ // d=>CAy=AQE (so le trong)

=>C1 = AQE=>tam giác CEQ cân tại E =>EQ=EC (2)

Hai tiếp tuyến EB và EC cắt nhau tại E=>EB=EC (3)

Từ (1)(2)(3)=>EP=EQ(đpcm)

4. Tam giác ABC và tam giác AQP có:

ACB = APQ (cùng bằng Bax) và PAQ chung=>Tam giác ABC với tam giác AQP đồng

dạng (g.g)

$=>\frac{AC}{AP}=\frac{BC}{PQ}=\frac{2.MC}{2.PE}=\frac{MC}{PE}=>\frac{PE}{CM}=\frac{PA}{CA}$

Tam giác AEP và tam giác AMC có:

$\frac{PE}{CM}=\frac{PA}{CA}$(cmt)

APE=ACM(cùng bằng Bax)

=> Tam giác AEP đồng dạng với tam giác AMC (c.g.c)=>PAE=MAC(đpcm)

5. Gọi N là giao điểm của tia AM và (O) ta có:

BAN = BCN (cùng chắn BN)

AMB = NMC (đối đỉnh)

=>tam giác AMB đồng dạng CMN (g.g)

$=>\frac{AM}{CM}=\frac{MB}{MN}=>AM.MN=MB.MC=\frac{BC}{2}.\frac{BC}{2}=\frac{B{C}^2}{4}$(*)

(O) có: Góc PAE=MAC(cmt)=>góc BAD=NAC

Góc BAD nội tiếp chắn cung BD

Góc NAC nội tiếp chắn cung CN

=>BD=CN

Tam giác EBC cân tại E góc EBM = ECM góc EBD + DBM = ECN + NCM

Mà EBD = ECN (chắn 2 cung bằng nhau) DBM = NCM

Tam giác BDM và tam giác CNM có:

MB=MC

DBM=NCM

BD=CN

=> Tam giác BDM= tam giác CNM

=>MD=MN(**)

Từ (*) và (**) => AM.MD = $\frac{B{C}^2}{4}$(đpcm)

......................................................

......................................................

......................................................