Dạng 3: Giải toán bằng biểu đồ Vencó đáp án
-
550 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tập hợp A có 9 phần tử, tập hợp B có 5 phần tử, tập hợp A ∩ B có 3 phần tử. Tính số phần tử của tập hợp A \ B.
Xem đáp án
Đáp án đúng là: B.
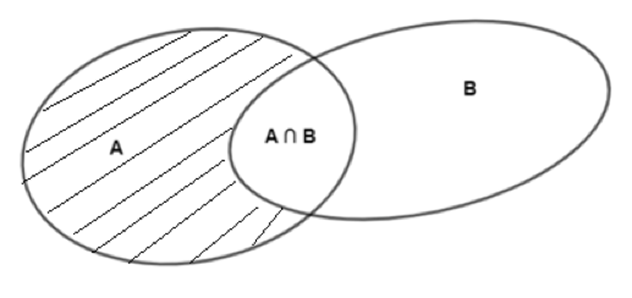
Ta có:
+ Tập hợp A gồm 9 phần tử nên n(A) = 9.
+ Tập hợp B gồm 5 phần tử nên n(B) = 5.
+ Tập hợp A ∩ B gồm 3 phần tử nên n(A ∩ B) = 3.
Vì hiệu của hai tập hợp A và B là tập hợp những phần tử thuộc A mà không thuộc B (phần gạch chéo trên hình vẽ) nên ta có:
n(A \ B) = n(A) – n(A ∩ B) = 9 – 3 = 6.
Câu 2:
17/07/2024Cho tập hợp A có 15 phần tử, tập hợp B có 10 phần tử, tập hợp A ∩ B có 5 phần tử. Tính số phần tử của tập hợp B \ A.
Xem đáp án
Đáp án đúng là: D.
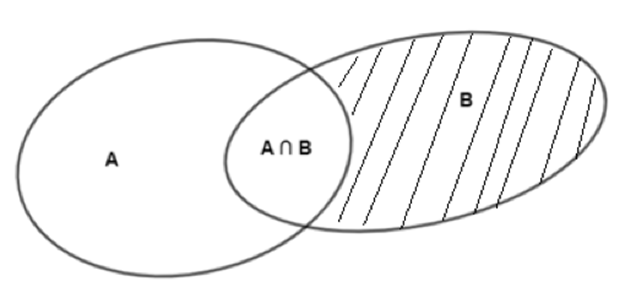
Ta có:
+ Tập hợp A gồm 15 phần tử nên n(A) = 15.
+ Tập hợp B gồm 10 phần tử nên n(B) = 10.
+ Tập hợp A ∩ B gồm 5 phần tử nên n(A ∩ B) = 5.
Vì hiệu của hai tập hợp B và A là tập hợp những phần tử thuộc B mà không thuộc A (phần gạch chéo trên hình vẽ) nên ta có:
n(B \ A) = n(B) – n(A ∩ B) = 10 – 5 = 5.
Câu 3:
13/07/2024Cho tập hợp A có 12 phần tử, tập hợp B có 15 phần tử, tập hợp A ∩ B có 6 phần tử. Tính số phần tử của tập hợp A ∪ B.
Xem đáp án
Đáp án đúng là: B.
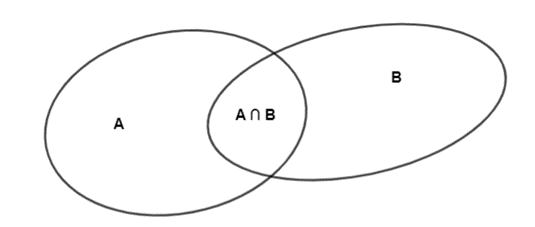
– Ta có:
+ Tập hợp A gồm 12 phần tử nên n(A) = 12.
+ Tập hợp B gồm 15 phần tử nên n(B) = 15.
+ Tập hợp A ∩ B gồm 6 phần tử nên n(A ∩ B) = 6.
– Ta có tập hợp A ∪ B là tập hợp các phần tử thuộc tập hợp A hoặc thuộc tập hợp B.
Do đó số phần tử của tập hợp A ∪ B là:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 12 + 15 – 6 = 21.
Câu 4:
13/07/2024Cho tập hợp A có 19 phần tử, tập hợp B có 22 phần tử, tập hợp các phần tử hoặc thuộc A hoặc thuộc B gồm 35 phần tử. Tính số phần tử của tập hợp A vừa thuộc A vừa thuộc B.
Xem đáp án
Đáp án đúng là: A.
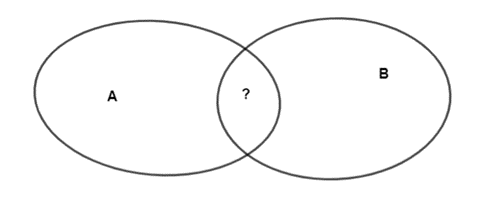
– Ta có:
+ Tập hợp A gồm 19 phần tử nên n(A) = 19.
+ Tập hợp B gồm 22 phần tử nên n(B) = 22.
+ Tập hợp các phần tử hoặc thuộc A hoặc thuộc B là A ∪ B.
Do đó, n(A ∪ B) = 35.
Tập hợp các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B được kí hiệu là A ∩ B.
Do đó, n(A ∩ B) = n(A) + n(B) – n(A ∪ B) = 19 + 22 – 35 = 6.
Vậy có 6 phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B.
Câu 5:
14/07/2024Để tổ chức một buổi đi liên hoan, lớp 10B lập một bài khảo sát. Kết quả là có 20 bạn rảnh vào thứ 7, 25 bạn rảnh vào chủ nhật. Trong đó có 8 bạn rảnh cả hai ngày.
Hỏi có bao nhiêu học sinh chỉ rảnh vào ngày thứ 7?
Xem đáp án
Đáp án đúng là: C.
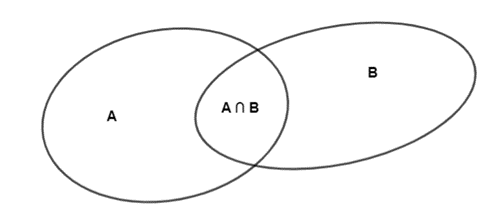
Gọi A là tập hợp các bạn rảnh vào thứ 7, B là tập hợp các bạn rảnh vào chủ nhật.
Do đó A ∩ B là tập hợp các bạn vừa rảnh thứ 7 vừa rảnh chủ nhật.
Ta có:
+ 20 bạn rảnh vào thứ 7 nên n(A) = 20.
+ 25 bạn rảnh vào chủ nhật nên n(B) = 25.
+ 8 bạn rảnh cả hai ngày nên n(A ∩ B) = 8.
Ta lại có tập hợp các bạn học sinh chỉ rảnh vào ngày thứ 7 là A \ B.
Vì hiệu của hai tập hợp A và B là tập hợp những phần tử thuộc A mà không thuộc B nên ta có:
n(A \ B) = n(A) – n(A ∩ B) = 20 – 8 = 12.
Vậy có 12 bạn chỉ rảnh thứ 7.
Câu 6:
13/07/2024Trong môn thể dục, lớp 10C có 21 bạn đăng kí học bơi, 30 bạn đăng kí học môn cầu lông, 10 bạn vừa đăng kí học bơi vừa đăng kí cầu lông. Hỏi lớp 10C có tất cả bao nhiêu bạn, biết mỗi bạn đều đang kí học bơi hoặc học cầu lông?
Xem đáp án
Đáp án đúng là: B.
Gọi A là tập hợp các bạn đăng kí học bơi, B là tập hợp các bạn đăng kí học cầu lông.
Do đó A ∩ B là tập hợp các bạn vừa đăng kí học bơi vừa đăng kí cầu lông.
– Ta có:
+ 21 bạn đăng kí học bơi nên n(A) = 21.
+ 30 bạn đăng kí học môn cầu lông nên n(B) = 30.
+ 10 bạn vừa đăng kí học bơi vừa đăng kí cầu lông nên n(A ∩ B) = 10.
– Tập hợp các bạn học sinh trong lớp 10C cũng là tập hợp các bạn hoặc đăng kí học bơi hoặc đăng kí học cầu lông.
Do đó, tập hợp các bạn học sinh trong lớp 10C là A ∪ B.
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 21 + 30 – 10 = 41.
Vậy lớp 10C có 41 bạn.
Câu 7:
13/07/2024Lớp 10D có 22 học sinh thích chơi bóng đá, 17 học sinh thích chơi môn cờ vua, 7 học sinh thích cả hai môn bóng đá và cờ vua và 10 bạn không thích chơi môn nào cả. Hỏi lớp 10D có bao nhiêu học sinh?
Xem đáp án
Đáp án đúng là: D.
Gọi A là tập hợp các bạn thích chơi bóng đá, B là tập hợp các bạn thích chơi cờ vua, C là tập hợp các bạn không thích chơi môn nào (phần màu xanh trên hình).
Do đó A ∩ B là tập hợp các bạn vừa thích chơi bóng đá vừa thích chơi cờ vua.
– Ta có:
+ 22 học sinh thích chơi bóng đá nên n(A) = 22.
+ 17 học sinh thích chơi môn cờ vua nên n(B) = 17.
+ 10 bạn không thích chơi môn nào nên n(C) = 10.
+ 7 học sinh thích cả hai môn bóng đá và cờ vua nên n(A ∩ B) = 7.
– Tập hợp các bạn học sinh trong lớp 10D cũng là tập hợp các bạn thích chơi bóng đá hoặc thích chơi cờ vua hoặc không thích chơi môn nào cả.
Vậy tập hợp các bạn học sinh trong lớp 10C là A ∪ B ∪ C.
Ta có: n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) = 22 + 17 + 10 – 7 = 42
Do đó lớp 10D có 42 bạn.
Câu 8:
13/07/2024Lớp 10T có 23 học sinh thích học môn Toán, 11 học sinh thích học môn Tiếng Anh, 5 học sinh thích học cả hai môn Toán và Tiếng Anh và 12 bạn không thích học môn nào cả (trong hai môn Toán và Tiếng Anh). Hỏi lớp 10T có bao nhiêu học sinh chỉ thích một môn?
Xem đáp án
Đáp án đúng là: C.
Số bạn chỉ thích học môn Toán mà không thích học Tiếng Anh là : 23 – 5 = 18 (bạn).
Số bạn chỉ thích học môn Tiếng Anh mà không thích học môn Toán là : 11 – 5 = 6 (bạn).
Vậy số bạn chỉ thích học học một môn (trong hai môn Toán và Tiếng Anh) là
18 + 6 = 24 (bạn).
Câu 9:
13/07/2024 Xem đáp án
Đáp án đúng là: A.
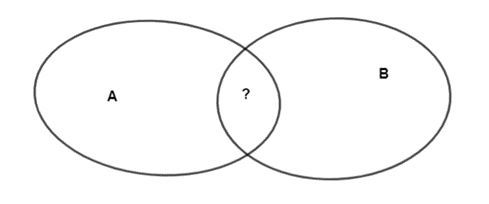
– Ta có:
+ Tập hợp A gồm 10 phần tử nên n(A) = 10.
+ Tập hợp B gồm 12 phần tử nên n(B) = 12.
+ Tập hợp các phần tử hoặc thuộc A hoặc thuộc B là A ∪ B hay n(A ∪ B) = 20.
Tập hợp các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B được kí hiệu là A ∩ B.
Vậy n(A ∩ B) = n(A) + n(B) – n(A ∪ B) = 10 + 12 – 20 = 2.
Câu 10:
22/07/2024Cho tập hợp A có 18 phần tử, tập hợp B có 25 phần tử, tập hợp A ∩ B có 9 phần tử. Tính số phần tử chỉ thuộc tập hợp A.
Xem đáp án
Đáp án đúng là: B.
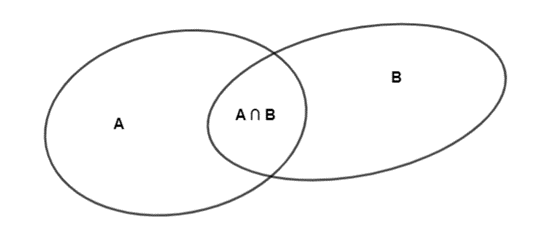
Ta có:
+ Tập hợp A gồm 18 phần tử nên n(A) = 18.
+ Tập hợp B gồm 25 phần tử nên n(B) = 25.
+ Tập hợp A ∩ B gồm 9 phần tử nên n(A ∩ B) = 9.
Ta lại có tập hợp các phần tử chỉ thuộc A cũng là hiệu của hai tập hợp A và B nên ta có:
n(A \ B) = n(A) – n(A ∩ B) = 18 – 9 = 9.
Vậy có 9 phần tử chỉ thuộc tập hợp A.