Trắc nghiệm Toán 10 CTST Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (Phần 2)
Trắc nghiệm Toán 10 CTST Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (Thông hiểu)
-
534 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: 2x – y – 1 ≥ 0.
Vẽ đường thẳng d1: 2x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 1).
Xét điểm O(0; 0) ∉ d1, ta có: 2.0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình 2x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d1) không chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: 4x – 3y – 2 ≤ 0.
Vẽ đường thẳng d2: 4x – 3y – 2 = 0 đi qua hai điểm (2; 2) và (–1; –2).
Xét điểm O(0; 0) ∉ d2, ta có: 4.0 – 3.0 – 2 = –2 < 0 nên miền nghiệm của bất phương trình 4x – 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1 và d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
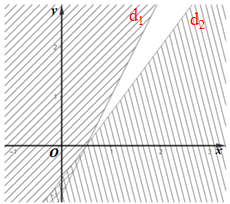
Vậy ta chọn phương án C.
Câu 2:
23/07/2024Cho hệ bất phương trình: {x+y−2≥0x−3y+3<0. Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
• Xét cặp số (1; 2):
Ta có: {1+2−2=1≥01−3.2+3=−2<0 nên cặp số (1; 2) thỏa mãn đồng thời cả hai bất phương trình của hệ.
Do đó cặp số (1; 2) là nghiệm của hệ bất phương trình. Khi đó A sai.
• Xét cặp số (34;54):
{34+54−2=0≥034−3.54+3=0 nên cặp số (34;54) không thỏa mãn đồng thời cả hai bất phương trình của hệ.
Do đó cặp số (34;54) không là nghiệm của hệ bất phương trình nên miền nghiệm của hệ không chứa điểm (34;54). Khi đó C sai.
• Miền nghiệm của hệ bất phương trình là miền không kể bờ là đường thẳng x – 3y + 3 = 0. Do đó B sai.
• Miền nghiệm của hệ bất phương trình là miền kể cả bờ là đường thẳng x + y – 2 = 0. Do đó miền nghiệm của hệ chứa tất cả các điểm nằm trên đường thẳng x + y – 2 = 0.
Khi đó D đúng.
Vậy ta chọn phương án D.
Câu 3:
13/07/2024Cho hệ bất phương trình: {0≤y≤4x≥0x-y-1≤0. Miền nghiệm của hệ bất phương trình là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: {0≤y≤4x≥0x−y−1≤0x+2y−10≤0⇔{y≥0y≤4x≥0x−y−1≤0x+2y−10≤0
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: y ≥ 0.
Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: y = 0) chứa điểm (0; 1).
• Biểu diễn miền nghiệm của bất phương trình: y ≤ 4.
Miền nghiệm của bất phương trình y ≤ 4 là nửa mặt phẳng (kể cả đường thẳng d2: y = 4) chứa điểm (0; 1).
• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.
Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d3: x = 0) chứa điểm (1; 0).
• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.
Vẽ đường thẳng d4: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d4) chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.
Vẽ đường thẳng d5: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d5) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3, d4 và d5) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
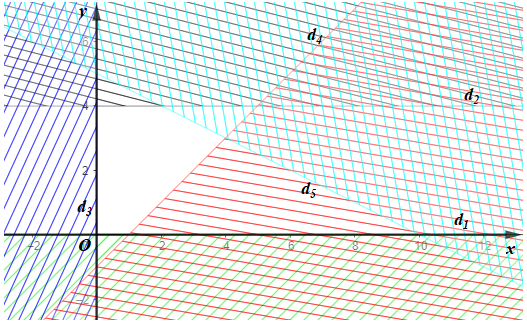
Vậy miền nghiệm của hệ bất phương trình là miền ngũ giác.
Ta chọn phương án C.
Câu 4:
20/07/2024Cho các đường thẳng d1: 3x – 4y + 12 = 0, d2: x + y – 5 = 0 và d3: x + 1 = 0.
Miền không gạch chéo (kể cả bờ d1, d2, d3) trong hình vẽ bên dưới là miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình dưới đây?

 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta xét điểm O(0; 0):
{3.0−4.0+12=12>00+0−5=−5<00+1=1>0.
Do đó điểm O(0; 0) thuộc miền nghiệm của các bất phương trình:
{3x−4y+12>0x+y−5<0x+1>0.
Quan sát hình vẽ ta thấy miền nghiệm có:
• Nửa mặt phẳng bờ là đường thẳng d1 (3x – 4y + 12 = 0) có chứa điểm O;
• Nửa mặt phẳng bờ là đường thẳng d2 (x + y – 5 = 0) có chứa điểm O;
• Nửa mặt phẳng bờ là đường thẳng d3 (x + 1 = 0) không chứa điểm O.
Do đó hệ bất phương trình cần tìm là {3x−4y+12≥0x+y−5≤0x+1≤0.
Vậy ta chọn phương án A.
Câu 5:
16/07/2024Cho hệ bất phương trình: {2x+3y+6≥0x≤02x−3y+1≥0. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
• Xét điểm O(0; 0) ta có: {2.0+3.0+6=6≥00≤02.0−3.0+1=1≥0
Nên cặp số (0; 0) thỏa mãn đồng thời cả ba bất phương trình của hệ.
Do đó miền nghiệm của hệ chứa gốc tọa độ O. Khi đó C là khẳng định đúng.
• Hệ bất phương trình {2x+3y+6≥0x≤02x−3y+1≥0 có miền nghiệm kể cả bờ 2x – 3y + 1 = 0.
Do đó D là khẳng định đúng.
• Biểu diễn miền nghiệm của hệ bất phương trình:
Miền nghiệm của bất phương trình 2x + 3y + 6 ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: 2x + 3y + 6 = 0) chứa điểm O(0; 0).
Miền nghiệm của bất phương trình x ≤ 0 là nửa mặt phẳng (kể cả đường thẳng d2: x = 0) chứa điểm (–1; 0).
Miền nghiệm của bất phương trình 2x – 3y + 1 ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d3: 2x – 3y + 1 = 0) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
Miền nghiệm là miền tam giác ABC với A(0; –2), B(0;13), C(−74;−56). Khi đó A là khẳng định đúng.
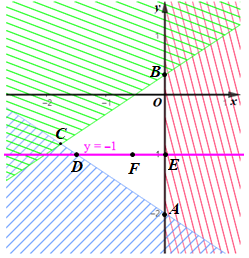
Vẽ đường thẳng y = –1 ta thấy đường thẳng y = –1 cắt cạnh AC tại D và cắt cạnh AB tại E và cắt miền trong tam giác ABC tại vô số điểm F. Do đó đường thẳng y = –1 cắt miền tam giác ABC tại vô số điểm.
Khi đó B là khẳng định sai.
Vậy ta chọn phương án B.
Câu 6:
21/07/2024Cho hệ bất phương trình {3x+2y<1(1)x+23y<1(2). Gọi S1 là miền nghiệm của bất phương trình (1), S2 là miền nghiệm của bất phương trình (2).
Cho các phát biểu sau:
(I) Miền nghiệm của hệ bất phương trình là S1;
(II) Miền nghiệm của hệ bất phương trình là S2;
(III) Hai bất phương trình của hệ có cùng miền nghiệm.
Số phát biểu đúng là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là:
Ta có {3x+2y<1(1)x+23y<1(2)⇔{3x+2y−1<03x+2y−3<0
Biểu diễn miền nghiệm của hệ {3x+2y−1<03x+2y−3<0 trên mặt phẳng Oxy.
• Miền nghiệm của bất phương trình 3x + 2y – 1 < 0 là nửa mặt phẳng (kể cả bờ d1: 3x + 2y – 1 = 0) chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình 3x + 2y – 3 < 0 là nửa mặt phẳng (kể cả bờ d2: 3x + 2y – 3 = 0) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
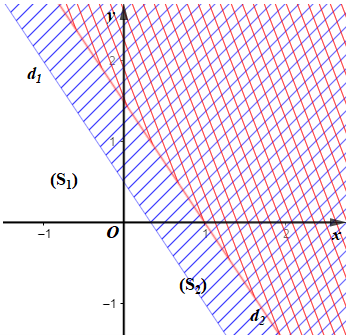
Do đó miền nghiệm của hệ bất phương trình là miền (S1) nên chỉ có (I) đúng.
Vậy ta chọn phương án B.
Câu 7:
15/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Để hệ bất phương trình {x−2y<0mx2+3y>02x−(m2−m)y2≤0 là hệ bất phương trình bậc nhất hai ẩn x và y thì hệ số của x2 và y2 bằng 0.
Tức là {m=0m2−m=0⇔{m=0[m=0m=1⇔m=0.
Vậy ta chọn phương án A.
Câu 8:
13/07/2024Cho hệ bất phương trình {x−2y<0x+3y>−2 và các điểm A(–1; 0), B(1; 0), C(–3; 4) và D(0; 3). Miền nghiệm của hệ bất phương trình chứa bao nhiêu điểm trong bốn điểm trên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
• Xét điểm A(–1; 0) ta có: {−1−2.0=−1<0−1+3.0=−1>−2 thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình chứa điểm A(–1; 0).
• Xét điểm B(1; 0) ta có: {1−2.0=1>01+3.0=1>−2 không thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình không chứa điểm B(1; 0).
• Xét điểm C(–3; 4) ta có: {−3−2.4=−11<0−3+3.4=9>−2 thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình chứa điểm C(–3; 4).
• Xét điểm D(0; 3) ta có: {0−2.3=−6<00+3.3=9>−2 thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình không chứa điểm D(0; 3).
Vậy miền nghiệm của hệ bất phương trình chứa ba điểm A, C, D trong 4 điểm.
Ta chọn phương án C.
Bài thi liên quan
-
Trắc nghiệm Toán 10 CTST Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (Nhận biết)
-
7 câu hỏi
-
30 phút
-
-
Trắc nghiệm Toán 10 CTST Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (Vận dụng)
-
5 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (555 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2. Hệ bất phương trình bậc nhất hai ẩn có đáp án (Phần 2) (533 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 CTST Bài tập cuối chương 2 có đáp án (Phần 2) (551 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Phần 2) (486 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (386 lượt thi)
- Trắc nghiệm Toán 10 Ôn tập chương 2 có đáp án (311 lượt thi)
