Giải SGK Toán 8 KNTT Bài tập cuối chương 3 có đáp án
Giải SGK Toán 8 KNTT Bài tập cuối chương 3 có đáp án
-
123 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
09/07/2024Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì góc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
 Xem đáp án
Xem đáp án
* Khẳng định A sai vì có xảy ra trường hợp tứ giác mà không có góc tù.
Chẳng hạn như hình chữ nhật có bốn góc vuông, tức là hình chữ nhật không có góc tù.
* Khẳng định B.
Tứ giác có ba góc nhọn thì tổng số đo của ba góc bé hơn: 90o . 3 = 270o.
Khi đó, góc còn lại sẽ lớn hơn: 360o – 270o = 90o.
Do đó, góc còn lại là góc tù nên khẳng định B đúng.
* Khẳng định C sai vì có thể xảy ra trường hợp tứ giác có hai góc tù, một góc vuông và một góc nhọn.
Ví dụ: Tứ giác ABCD có
* Khẳng định D sai vì có thể xảy ra trường hợp tứ giác có ba góc tù.
Ví dụ: Tứ giác MNPQ có .
Vậy khẳng định B là đúng.
Câu 2:
12/07/2024Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
 Xem đáp án
Xem đáp án
Khẳng định a) sai vì tứ giác có hai đường chéo bằng nhau thì chưa chắc tứ giác đó là hình bình hành.
Câu 3:
21/07/2024b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
 Xem đáp án
Xem đáp án
Khẳng định b) sai vì tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành, còn tứ giác có hai cặp cạnh bằng nhau thì chưa khẳng định được là hình bình hành.
Câu 4:
16/07/2024c) Tứ giác có ba góc vuông là hình chữ nhật.
 Xem đáp án
Xem đáp án
Khẳng định c) đúng.
Tứ giác có ba góc vuông thì số đo của góc còn lại là:
360o – 90o . 3 = 90o.
Khi đó, số đo của góc còn lại cũng là góc vuông.
Do đó, tứ giác đã cho có bốn góc vuông nên tứ giác đó là hình chữ nhật.
Câu 5:
20/07/2024d) Tứ giác có ba cạnh bằng nhau là hình thoi.
 Xem đáp án
Xem đáp án
Khẳng định d) sai vì tứ giác có bốn cạnh bằng nhau mới là hình thoi.
Vậy khẳng định b) đúng; các khẳng định a), b), d) sai.
Câu 6:
12/07/2024Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
 Xem đáp án
Xem đáp án
a) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Nên tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
Do đó khẳng định a) đúng.
Câu 7:
23/07/2024b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
b) Hình bình hành có hai cặp cạnh đối diện bằng nhau.
Nên tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
Do đó khẳng định b) là đúng.
 Xem đáp án
Xem đáp án
b) Hình bình hành có hai cặp cạnh đối diện bằng nhau.
Nên tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
Do đó khẳng định b) là đúng.
Câu 8:
09/07/2024c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
 Xem đáp án
Xem đáp án
c) Tứ giác có hai cạnh song song là hình thang.
Hình thang có và hai đường chéo bằng nhau là hình thang cân.
Nên tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
Do đó khẳng định c) đúng.
Câu 9:
21/07/2024 Xem đáp án
Xem đáp án
d) Tứ giác có hai cạnh đối vừa song song vừa bằng nhau là hình bình hành.
Do đó khẳng định d) sai.
Vậy các khẳng định a), b), c) đúng; khẳng định d) sai.
Câu 10:
16/07/2024Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.59).

 Xem đáp án
Xem đáp án
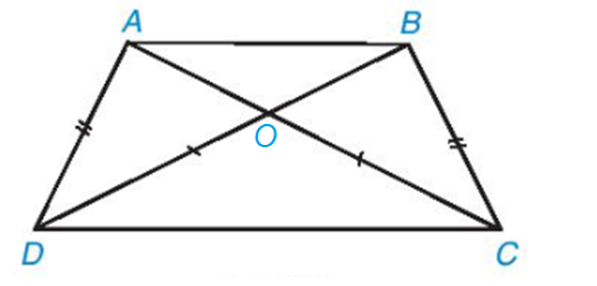
Gọi O là giao điểm của AC và BD.
Xét ∆ABC và ∆BAD có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh AB chung
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra (hai góc tương ứng).
Xét ∆ACD và ∆BDC có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh CD chung
Do đó ∆ADC = ∆BCD (c.c.c)
Suy ra (hai góc tương ứng).
Xét ∆OAD và ∆OBC có:
(chứng minh trên)
AD = BC (giả thiết)
(chứng minh trên)
Do đó ∆OAD = ∆OBC (g.c.g).
Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).
Khi đó, các tam giác OAB, OCD là tam giác cân tại O.
Suy ra .
Xét ∆OAB và ∆OCD cân tại O có:
• (hai góc đối đỉnh)
•
•
Suy ra mà hai góc này ở vị trí so le trong.
Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Các bài thi hot trong chương
- Trắc nghiệm Toán 8 KNTT Bài 14. Hình thoi và hình vuông (294 lượt thi)
- Trắc nghiệm Toán 8 KNTT Bài 12. Hình bình hành (264 lượt thi)
- Trắc nghiệm Toán 8 KNTT Bài 11. Hình thang cân (258 lượt thi)
- Trắc nghiệm Toán 8 KNTT Bài 13. Hình chữ nhật (239 lượt thi)
- Trắc nghiệm Toán 8 KNTT Bài 10. Tứ giác (202 lượt thi)
