Giải SGK Toán 11 CD Bài 1. Đường thẳng và mặt phẳng trong không gian
Giải SGK Toán 11 CD Bài 1. Đường thẳng và mặt phẳng trong không gian
-
93 lượt thi
-
22 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Sân vận động Old Trafford (Hình 2) ở thành phố Manchester, có biệt danh là “Nhà hát của những giấc mơ”, với sức chứa 75 635 người, là sân vận động lớn thứ hai ở Vương quốc Anh.

Quan sát Hình 2 và cho biết mặt sân vận động thường được làm phẳng hay cong.
 Xem đáp án
Xem đáp án
Lời giải:
Mặt của sân vận động là mặt phẳng.
Câu 2:
29/06/2024 Xem đáp án
Xem đáp án
Lời giải:
Các ví dụ trong thực tiễn nói về một phần của mặt phẳng là: Mặt bàn, mặt ghế, nền nhà, ...
Câu 3:
17/07/2024
 Xem đáp án
Xem đáp án
Lời giải:
Nếu coi mặt sân Napoléon là một phần của mặt phẳng (P) thì đỉnh của kim tự tháp không thuộc mặt phẳng (P).
Câu 4:
20/07/2024 Xem đáp án
Xem đáp án
Lời giải
Câu 5:
23/07/2024Hình 9 là hình ảnh xà ngang trong môn Nhảy cao.
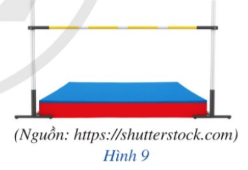
Quan sát Hình 9 và cho biết ta cần bao nhiêu điểm đỡ để giữ cố định được xà ngang đó.
 Xem đáp án
Xem đáp án
Lời giải
Dựa vào Hình 9, cần có 2 điểm đỡ để giữ cố định được xà ngang.
Câu 6:
18/07/2024
 Xem đáp án
Xem đáp án
Lời giải
Vì ba điểm chân kiềng sẽ luôn luôn nằm trên một mặt phẳng.
Câu 7:
07/07/2024
 Xem đáp án
Xem đáp án
Lời giải
Giao giữa bức tường chứa bảng với nền nhà là một đường thẳng.
Câu 8:
20/07/2024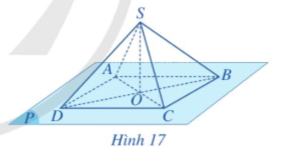
 Xem đáp án
Xem đáp án
Lời giải
Ta có: S ∈ (SAC) và S ∈ (SBD)
Do đó giao tuyến của hai mặt phẳng (SAC) và (SBD) đi qua điểm S.
Ta lại có: O ∈ AC mà AC ⊂ (SAC) nên O ∈ (SAC);
O ∈ BD mà BD ⊂ (SBD) nên O ∈ (SBD).
Do đó giao tuyến của hai mặt phẳng (SAC) và (SBD) đi qua điểm O.
Khi đó giao tuyến của hai mặt phẳng (SAC) và (SBD) chính là đường thẳng SO.
Vậy (SAC) ∩ (SBD) = SO.
Câu 9:
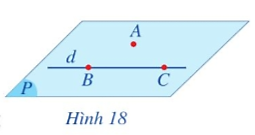
21/07/2024Cho điểm A không thuộc đường thẳng d. Lấy hai điểm B và C thuộc đường thẳng d (Hình 18).
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
 Xem đáp án
Xem đáp án
Lời giải
a) Dựa vào hình vẽ ta thấy mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d.
b) Có duy nhất một mặt phẳng đi qua điểm A và đường thẳng d.Câu 10:
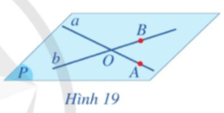
19/07/2024Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19).
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
 Xem đáp án
Xem đáp án
Lời giải
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b.
b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b.
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
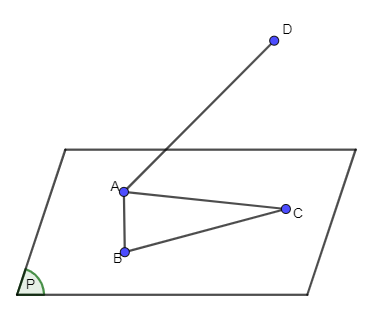
Do tam giác ABC nằm trên mặt phẳng (P) nên (P) đi qua ba điểm A, B, C.
Mà có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Do đó qua ba điểm A, B, C xác định được duy nhất mặt phẳng (P).
Mà điểm D không thuộc mặt phẳng (P) nên bốn điểm A, B, C, D không cùng nằm trên một đường thẳng.
Vậy không xác định được mặt phẳng nào đi qua hai đường thẳng AD và BC .
Câu 12:
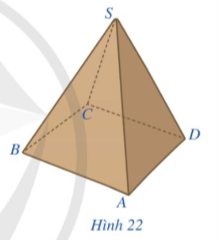
07/07/2024Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?
b) Mỗi mặt phẳng của hộp quà lưu niệm có dạng hình gì?
 Xem đáp án
Xem đáp án
Lời giải
a) Đỉnh S không nằm trong mặt phẳng (ABCD).
b) Các mặt bên của hộp quà lưu niệm có dạng hình tam giác cân.
Mặt đáy của hộp quà lưu niệm có dạng hình vuông.
Câu 13:
08/07/2024Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB.
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC).
 Xem đáp án
Xem đáp án
Lời giải
a)
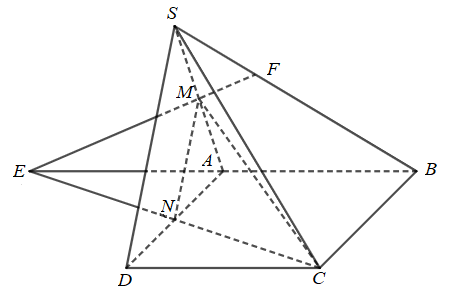
+) Trong mặt phẳng (ABCD): Gọi giao điểm của AB với NC là E.
Mà NC ⊂ (CMN)
Suy ra: (CMN) ∩ AB = {E}.
+) Trong mặt phẳng (SAB): Kéo dài EM cắt AB tại F.
Mà EM ⊂ (CMN)
Suy ra (SAB) ∩ EM = {F}.
b)
+) Ta có: M ∈ SA mà SA ⊂ (SAB) nên M ∈ (SAB);
M ∈ CM mà CM ⊂ (CMN) nên M ∈ (CMN).
Do đó M là giao điểm của hai mặt phẳng (SAB) và (CMN).
Ta lại có: AB ∩ CN = {E};
AB ⊂ (SAB);
CN ⊂ (CMN).
Do đó E là giao điểm của hai mặt phẳng (SAB) và (CMN).
Vì vậy (SAB) ∩ (CMN) = EM.
+) Ta có: C ∈ SC mà SC ⊂ (SBC);
C ∈ CM mà CM ⊂ (CMN).
Do đó C là giao điểm của hai mặt phẳng (SBC) và (CMN).
Ta lại có: SB ∩ EM = {F};
SB ⊂ (SBC);
EM ⊂ (CMN).
Do đó F là giao điểm của hai mặt phẳng (SBC) và (CMN).
Vì vậy (SBC) ∩ (CMN) = CF.
Câu 14:
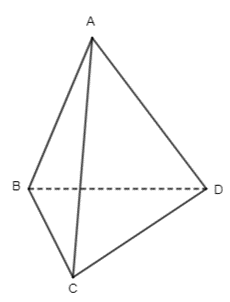
12/07/2024Hình 25 là hình ảnh của khối rubik tam giác (Pyraminx). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?

 Xem đáp án
Xem đáp án
Lời giải
a) Khối rubik tam giác có 4 đỉnh. Các đỉnh không cùng nằm trong một mặt phẳng.
b) Khối rubik tam giác có 4 mặt. Mỗi mặt của khối rubik tam giác là hình tam giác.
Câu 15:
06/01/2025Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho AMAB=13,ANAD=23,BPBC=34.
a) Xác định E, F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP).
b) Chứng minh rằng các đường thẳng NE, PF và CD cùng đi qua một điểm.
 Xem đáp án
Xem đáp án
Lời giải
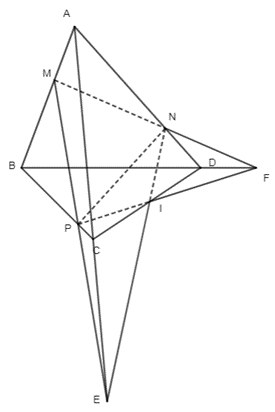
a)
+) Trong mặt phẳng (ABC), gọi giao điểm của MP với AC là E.
Mà MP ⊂ (MNP) nên (MNP) ∩ AC = {E}.
+) Trong mặt phẳng (ABD), gọi giao điểm của MN với BD là F.
Mà MP ⊂ (MNP) nên (MNP) ∩ BD = {F}.
b) • Ta có: N ∈ AD, mà AD ⊂ (ACD) nên N ∈ (ACD).
Lại có N ∈ (MNP)
Do đó N là giao điểm của (ACD) và (MNP).
Mặt khác: MP ∩ AC = {E};
MP ⊂ (MNP);
AC ⊂ (ACD).
Do đó E là giao điểm của (ACD) và (MNP).
Suy ra NE = (MNP) ∩ (ACD).
Trong mặt phẳng (ACD), nối NE cắt CD tại I.
Khi đó I ∈ CD và I ∈ NE ⊂ (MNP)
• Ta có: P ∈ BC, mà BC ⊂ (BCD) nên P ⊂ (BCD)
Lại có P ∈ (MNP)
Do đó P là giao điểm của (BCD) và (MNP).
Mặt khác: MN ∩ BD = {F}.
MN ⊂ (MNP);
BD ⊂ (BCD) .
Do đó F là giao điểm của (BCD) và (MNP).
Suy ra PF = (BCD) ∩ (MNP).
Trong mặt phẳng (BCD), gọi giao điểm của CD với PF là I.
Khi đó I ∈ CD, mà CD ⊂ (ACD)
I ∈ PF, mà PF ⊂ (MNP)
Suy ra I là giao điểm của hai mặt phẳng (MNP) và (ACD).
Hay I nằm trên giao tuyến NE của (MNP) và (ACD).
Do đó I ∈ NE.
Vậy ba đường thẳng NE, PF, CD cùng đi qua điểm I.Cách 1: Tìm giao điểm của hai đường thẳng, sau đó tiến hành chứng minh đường thẳng thứ ba cũng đi qua giao điểm đó.
Cách 2: Chứng minh một điểm bất kỳ cũng thuộc vào ba đường thẳng đó.
Cách 3: Sử dụng 1 trong những tính chất đồng quy trong tam giác như là:
* Ba đường thẳng có chứa các đường trung tuyến.
* Ba đường thẳng có chứa các đường phân giác.
* Ba đường thẳng có chứa các đường trung trực.
* Ba đường thẳng có chứa các đường các đường cao.
1. Ba đường thẳng đồng quy là gì?
Định nghĩa về ba đường thẳng đồng quy được diễn giải như sau: “Cho ba đường thẳng lần lượt là a, b, c không trùng với nhau. Nếu ba đường thẳng a,b,c cùng đi qua một điểm O nào đó thì ta sẽ gọi đó là đồng quy.
2. Tính chất của 3 đường thẳng đồng quy
– Nếu hai đường cao của tam giác cắt nhau tại một điểm cụ thể thì từ đó có thể suy ra đường cao thứ 3 cũng sẽ cùng đi qua giao điểm đó.
– Nếu ba đường trung tuyến của một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là trọng tâm của tam giác.
– Ba đường cao trong một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là trực tâm của tam giác.
– Nếu hai đường trung tuyến trong tam giác bất kỳ cắt nhau tại một điểm thì từ đó ta có thể suy ra đường trung tuyến thứ 3 chắc chắn cũng đi qua giao điểm đó. Trọng tâm sẻ chia đoạn thẳng trung tuyến thành 3 phần: Từ trọng tâm lên tới đỉnh chiếm tới 2/3 độ dài của trung tuyến đó.
– Nếu ba đường phân giác trong một tam giác đồng quy tại 1 điểm cụ thể thì điểm này sẽ được gọi là tâm của đường tròn nội tiếp tam giác.
– Nếu hai đường phân giác của tam giác cắt nhau tại một điểm cụ thể thì từ đó ta có thể suy ra đường phân giác thứ 3 cũng sẽ đi qua giao điểm đó. Giao điểm của 3 đường phân giác sẽ cách đều 3 cạnh của tam giác.
– Khi ba đường trung trực trong một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là tâm đường tròn ngoại tiếp tam giác.
– Nếu hai đường trung trực bên trong tam giác cắt nhau tại một điểm thì từ đó chúng ta có thể suy ra đường trung trực thứ 3 chắc chắn đi qua giao điểm đó. Giao điểm của 3 đường trung trực sẽ cách đều 3 đỉnh của tam giác.
3. Điều kiện để 3 đường thẳng đồng quy
- Định lý trọng tâm: Ba đường trung tuyến của tam giác cắt nhau tại một điểm. Đồng thời khoảng cách từ điểm này đến đỉnh gấp đôi khoảng cách từ điểm này đến trung điểm của cạnh đối diện. Giao điểm nói trên được gọi là trọng tâm của hình tam giác.
- Định lý tâm ngoại tiếp: các đường trung trực của ba cạnh của tam giác cắt nhau tại một điểm. Điểm này gọi là tâm ngoại tiếp của tam giác.
- Định lý trực tâm: Ba đường cao của tam giác cắt nhau tại một điểm. Điểm này được gọi là trực tâm của tam giác
- Định lý tâm nội tiếp: Ba đường phân giác trong của tam giác cắt nhau tại một điểm. Điểm này được gọi là tâm nội tuyến của tam giác.
- Định lý tâm bàng tiếp: Tia phân giác của góc trong của tam giác và tia phân giác của góc ngoài ở hai đỉnh còn lại cắt nhau tại một điểm. Điểm này gọi là tâm bàng tiếp của tam giác. Hình tam giác có 3 tâm bàng tiếp.
- Trọng tâm, trực tâm, tâm ngoại tiếp, tâm nội tiếp, tâm bàng tiếp đều là tâm của tam giác. Chúng đều có những mối liên hệ quan trọng đến hình tam giác.
Câu 16:
23/07/2024
 Xem đáp án
Xem đáp án
Lời giải
Công dụng của thước dẹt: Kiểm tra xem mặt tường đã phẳng chưa.
⇒ Áp thước vào mặt tường, nếu toàn bộ thước áp khít vào mặt tường thì mặt tường đã được trát phẳng, nếu thước không khít vào mặt tường thì cần bổ sung thêm vữa trát vào phần chưa khít đó.
Câu 17:
12/07/2024
 Xem đáp án
Xem đáp án
Lời giải
Hình biểu diễn của chặn giấy bằng gỗ là:
Câu 18:
12/07/2024 Xem đáp án
Xem đáp án
Lời giải
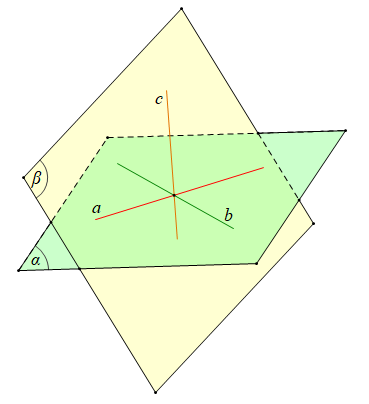
Giả sử a ∩ b = {I} và α = mp(a, b);
a ∩ c = {J} và β = mp(a, c);
b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.
Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.
α ∩ γ = b và đường thẳng b chính là đường thẳng IK.
β ∩ γ = c và đường thẳng c chính là đường thẳng JK.
Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)
Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.
Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.
Câu 19:
15/07/2024 Xem đáp án
Xem đáp án
Lời giải
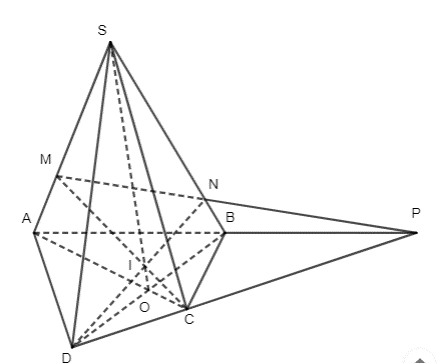
• Ta có: S ∈ (SAC) và S ∈ (SBD)
Do đó S là giao điểm của (SAC) và (SBD).
Mặt khác: AC ∩ BD = {O}.
AC ⊂ (SAC);
BD ⊂ (SBD).
Do đó O là giao điểm của (SAC) và (SBD).
Suy ra (SAC) ∩ (SBD) = SO.
• Trong mặt phẳng (DMNC) có:
DN ∩ MC = {I}.
DN ⊂ (SDB);
MC ⊂ (SAB).
Do đó I là giao điểm của (SAC) và (SBD).
Suy ra giao tuyến SO của hai mặt phẳng này đi qua điểm I.
Hay I ∈ SO.
Vậy S, I, O thẳng hàng.
Câu 20:
22/07/2024Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA = 2MS, NS = 2NC.
a) Xác định giao điểm của MN với mặt phẳng (ABC).
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).
 Xem đáp án
Xem đáp án
Lời giải
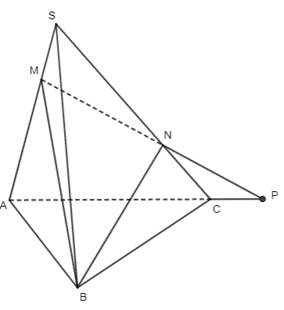
a) Trong mặt phẳng (SAC), gọi giao điểm của MN và AC là P.
Mà AC ⊂ (SAC)
Do đó MN ∩ (ABC) = {P}.
b) Ta có MN ∩ (ABC) = {P} nên P ∈ (ABC)
Lại có P ∈ MN mà MN ⊂ (BMN) nên P ∈ (BMN)
Do đó P là giao điểm của (BMN) và (ABC).
Mặt khác: B ∈ (BMN) và B ∈ (ABC).
Do đó B là giao điểm của (BMN) và (ABC).
Vì vậy (BMN) ∩ (ABC) = BP.
Câu 21:
19/07/2024Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với mặt phẳng (SAB).
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).
 Xem đáp án
Xem đáp án
Lời giải
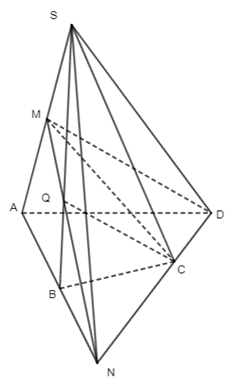
a) Trong mặt phẳng (ABCD) ta có: gọi giao điểm của AB và CD là N.
Mà AB ⊂ (SAB)
Do đó CD ∩ (SAB) = {N}.
b) Ta có: AB ∩ CD = {N};
AB ⊂ (SAB);
CD ⊂ (SCD)
Do đó N là giao điểm của (SAB) và (SCD).
Lại có: S ∈ (SAB) và S ∈ (SCD).
Nên S là giao điểm của (SAB) và (SCD).
Vì vậy (SAB) ∩ (SCD) = SN.
c) Ta có: C ∈ (SBC) và C ∈ (MCD).
Do đó C là giao điểm của (SBC) và (MCD).
Trong mặt phẳng (SAB), gọi Q là giao điểm của MN và SB.
Mà MN ⊂ (MCD) và SB ⊂ (SBC)
Suy ra Q là giao điểm của (SBC) và (MCD).
Vì vậy (SBC) ∩ (MCD) = CQ.
Câu 22:
23/07/2024Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.
a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).
b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: GMGA=GNGB=13.
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và GPGC=GQGD=13.
 Xem đáp án
Xem đáp án
Lời giải
a)
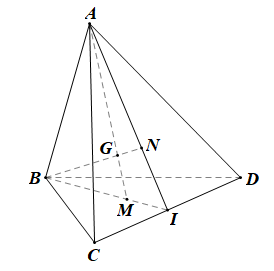
+) Xét tam giác BCD có: I là trung điểm của CD nên BI là đường trung tuyến.
Mà M là trọng tâm tam giác BCD nên BI đi qua M.
Do đó M ∈ BI.
Lại có AI ⊂ (ABI) nên M ∈ (ABI).
+) Xét tam giác ACD có: I là trung điểm của CD nên AI là đường trung tuyến.
Mà N là trọng tâm tam giác ACD nên AI đi qua N.
Do đó N ∈ AI.
Lại có BI ⊂ (ABI) nên N ∈ (ABI).
b) Trong DBCD có M là trọng tâm tam giác nên MIBI=13.
Trong DACD có N là trọng tâm tam giác nên NIAI=13.
Xét DABI có: NIAI=MIBI=13 nên MN // AB (theo định lí Thalès đảo).
Xét DABI và MN // AB, theo hệ quả định lí Thalès ta có MNAB=NIAI=MIBI=13.
Xét DABG và MN // AB, theo hệ quả định lí Thalès ta có GMGA=GNGB=MNAB=13.
c)
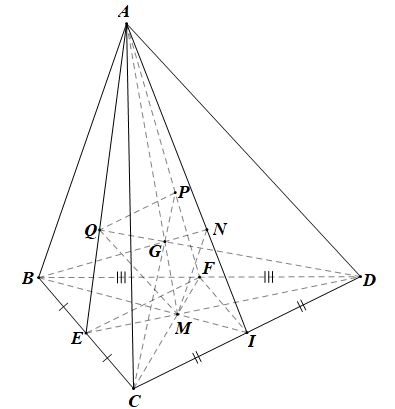
• Gọi G’ là giao điểm của AM và CP; G’’ là giao điểm của AM và DQ.
Chứng minh tương tự câu b, ta có: G′MG′A=G′PG′C=PMAC=13 và G″
Do đó \frac{{GM}}{{GA}} = \frac{{G'M}}{{G'A}} = \frac{{G''M}}{{G''A}} = \frac{1}{3}.
Mà G, G’, G’’ cùng nằm trên AM nên G ≡ G’ ≡ G’’.
Vậy các đường thẳng CP, DQ cùng đi qua điểm G.
• Xét tam giác ABC, kẻ đường trung tuyến AE (E ∈ BC).
Ta có: Q là trọng tâm DABC nên \frac{{AQ}}{{AE}} = \frac{2}{3}.
Xét tam giác ABD, kẻ đường trung tuyến AF (F ∈ BD).
Ta có: P là trọng tâm DABD nên \frac{{AP}}{{AF}} = \frac{2}{3}.
+) Trong mặt phẳng (AEF), có: \frac{{AQ}}{{AE}} = \frac{{AP}}{{AF}} = \frac{2}{3} nên PQ // EF (định lí Thalès đảo)
Mà EF // CD (đường trung bình tam giác BCD).
Suy ra PQ // CD
Theo hệ quả định lí Thalès ta có: \frac{{GP}}{{GC}} = \frac{{GQ}}{{GD}} = \frac{{QP}}{{CD}} = \frac{{QP}}{{2EF}} = \frac{1}{2}.\frac{2}{3} = \frac{1}{3}.
