Giải SBT Vật lý 11 KNTT Mô tả dao động điều hoà
Giải SBT Vật lý 11 KNTT Mô tả dao động điều hoà
-
133 lượt thi
-
14 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
03/07/2024Một chất điểm dao động điều hoà có chu kì T = 1 s. Tần số góc ω của dao động là
A. π(rad/s).
B. 2π(rad/s).
D. 2 (rad/s).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tần số góc: ω=2πT=2π1=2πrad/s
Câu 2:
20/07/2024Một chất điểm dao động điều hoà có tần số góc ω=10π(rad/s). Tần số của dao động là
A. 5Hz.
B. 10Hz.
C. 20Hz.
D. 5πHz. Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tần số f=ω2π=5Hz
Câu 3:
23/07/2024Một chất điểm dao động điều hoà. Trong thời gian 1 phút, vật thực hiện được 30 dao động. Chu kì dao động của chất điểm là
A. 2s.
B. 30s.
C. 0,5s.
D. 1s.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Chu kì T=tN=6030=2s
Câu 4:
20/07/2024Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: x=5√3cos(10πt+π3)(cm). Tần số của dao động là
A. 10Hz.
B. 20Hz.
C. 10πHz.
D. 5Hz.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Từ phương trình xác định được tần số góc ω=10πrad/s⇒f=ω2π=5Hz
Câu 5:
06/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Từ phương trình xác định được tần số góc ω=4πrad/s⇒T=2πω=0,5s
Câu 6:
15/07/2024Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: x=10cos(π3t+π2)(cm). Tại thời điểm t vật có li độ 6cm và đang hướng về vị trí cân bằng. Sau 9s kể từ thời điểm t thì vật đi qua li độ
A. 3cm đang hướng về vị trí cân bằng
B. −3cm đang hướng về vị trí biên.
C. 6cm đang hướng về vị trí biên.
D. −6cm đang hướng về vị trí cân bằng. Xem đáp án
Xem đáp án
Đáp án đúng là: D
Chu kì T=2πω=6s⇒t1=9s=1,5T.
Sau t1=1,5T vật ở vị trí như Hình 2.1G.
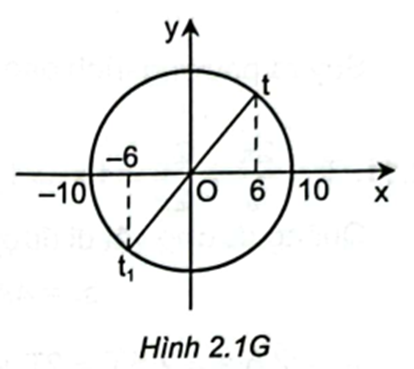
Do đó sau 9s kể từ thời điểm t thì vật đi qua li độ là −6cm và đang hướng về vị trí cân bằng.
Câu 7:
21/07/2024 Xem đáp án
Xem đáp án
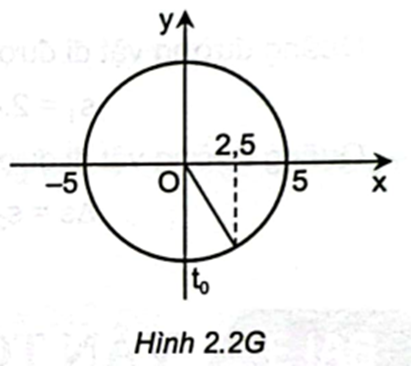
Chu kì T=2πω=15s.
Tại thời điểm ban đầu t = 0 thì x1=5cos(10π.0−π2)=0(cm)
Từ Hình 2.2G, ta thấy thời gian để vật đi được quãng đường 2,5 cm kể từ t=0 (từ x1=0 đến x2=2,5cm) là: t=T12=0,212=160s
Câu 8:
23/07/2024Đồ thị li độ theo thời gian của một chất điểm dao động điều hoà được mô tả như Hình 2.1
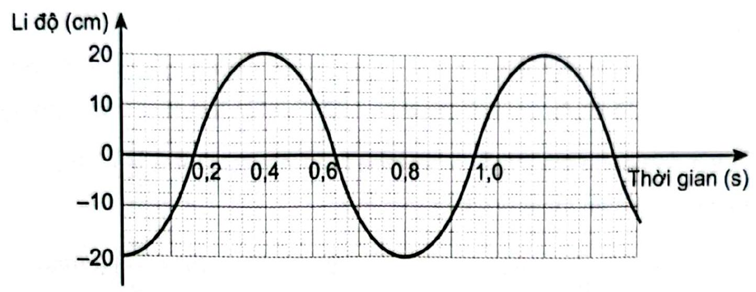
Xác định biên độ, chu kì và pha ban đầu của dao động.
 Xem đáp án
Xem đáp án
Biên độ A=20cm; chu kì T=0,8s; pha ban đầu φ=π(rad).
Câu 9:
13/07/2024Đồ thị li độ theo thời gian của một chất điểm dao động điều hoà được mô tả như Hình 2.1

Viết phương trình dao động.
 Xem đáp án
Xem đáp án
ω=2πT=2π0,8=2,5π(rad/s), phương trình dao động: x=20cos(2,5πt+π)(cm).
Câu 10:
23/07/2024Đồ thị li độ theo thời gian của một chất điểm dao động điều hoà được mô tả như Hình 2.1

Xác định li độ của chất điểm tại các thời điểm 0,4s,0,6s và 0,8s.
 Xem đáp án
Xem đáp án
Khi t=0,4s thì x=20cm;t=0,6s thì x=0;t=0,8s thì x=−20cm.
Câu 11:
12/07/2024Đồ thị li độ theo thời gian x1,x2 của hai chất điểm dao động điều hoà được mô tả như Hình 2.2
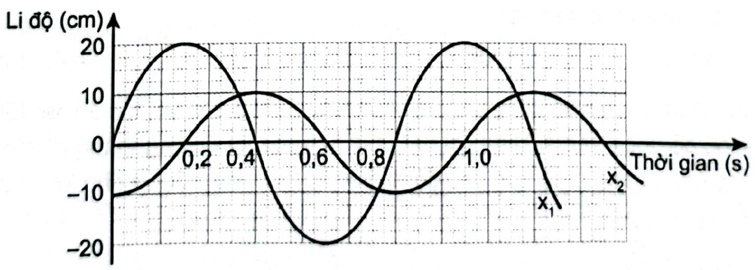
Xác định độ lệch pha giữa hai dao động.
 Xem đáp án
Xem đáp án
Từ đồ thị ta thấy:
Độ lệch pha theo thời gian: x1 sớm pha hơn x2 là T4.
Độ lệch pha theo góc: x1 sớm pha hơn x2 là Δφ=2πT.T4=π2 rad.
Câu 12:
20/07/2024Đồ thị li độ theo thời gian x1,x2 của hai chất điểm dao động điều hoà được mô tả như Hình 2.2

Viết phương trình dao động của hai chất điểm.
 Xem đáp án
Xem đáp án
A1=20cm;A2=10cm;T1=T2=0,8s
⇒ω1=ω2=2,5π(rad/s);φ1=−π2;φ2=−π.
⇒x1=20cos(2,5πt−π2)(cm);x2=10cos(2,5πt−π)(cm).
Câu 13:
12/07/2024Một chất điểm dao động điều hoà với chu kì T=2s. Trong 3s vật đi được quãng đường 60cm. Khi t=0 vật đi qua vị trí cân bằng và hướng về vị trí biên dương. Hãy viết phương trình dao động của vật.
 Xem đáp án
Xem đáp án
Có T=2s;t=3s=1,5T, do vậy quãng đường vật dao động đi được sau t=3s là:
s=4A+2A=6A=60cm⇒A=10cm;ω=2πT=2π2=π(rad/s); khi t=0 vật qua vị trí cân bằng và đang hướng về phía biên dương, nên φ=−π2.
Suy ra phương trình dao động của vật là: x=10cos(πt−π2)(cm).
Câu 14:
17/07/2024Một chất điểm dao động điều hoà theo phương trình x=10cos(2πt+5π6)(cm). Tính quãng đường vật đi được trong khoảng thời gian từ t1=1s đến t2=2,5s.
 Xem đáp án
Xem đáp án
T=2πω=2π2π=1s⇒t1=1s=1T.
Quãng đường vật đi được sau t1=1s là: s1=4A=40cm
t2=2,5s=2,5T=2T+T2.
Quãng đường vật đi được sau t2=2,5slà: s1=2.4A+2A=10A=100cm
Quãng đường vật đi được từ t1 đến t2 là: Δs=s2−s1=100−40=60cm.
Có thể bạn quan tâm
- Trắc nghiệm Vật lí 11 KNTT Bài 2: Mô tả dao động điều hòa (337 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Vật lí 11 KNTT Bài 1: Dao động điều hòa (546 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 3: Vận tốc, gia tốc trong giao động điều hòa (445 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 5: Động năng. Thế năng. Sự chuyển hóa giữa động năng và thế năng trong dao động điều hòa (358 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 4: Bài tập về giao động điều hòa (331 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 7: Bài tập về chuyển hóa năng lượng trong dao động điều hòa (320 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 6: Dao động tắt dần. Dao động cưỡng bức (285 lượt thi)
