Giải SBT Toán 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
Giải SBT Toán 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
-
131 lượt thi
-
18 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
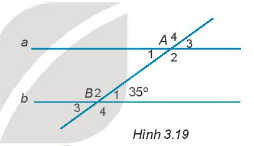
17/07/2024Cho Hình 3.19, biết a // b.
Tính số đo góc A1.
 Xem đáp án
Xem đáp án
Lời giải:
Vì a // b nên ^A1 và góc ^B1 là hai góc so le trong.
Do đó, ^A1 = ^B1 = 35o.
Câu 2:
17/07/2024So sánh góc A4 và B2.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì a // b nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có, ^A4 và ^B2 là hai góc đồng vị.
Do đó, ^A4 = ^B2.
Câu 3:
22/07/2024Tính số đo góc A2.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì ^A1 và ^A2 là hai góc kề bù nên ^A1 + ^A2 = 180o
Thay số: 35o + ^A2 = 180o
^A2 = 180o – 35o
^A2 = 145o.
Câu 4:
17/07/2024Giải thích tại sao Ax // By.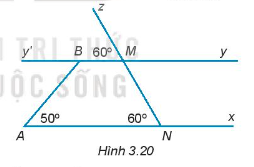
 Xem đáp án
Xem đáp án
Lời giải:
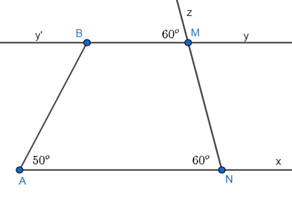
Ta có:
^zMy′=^zNA=60∘ mà ^zMy′ và ^zNA là hai góc đồng vị.
Do đó, Ax // By.
Câu 5:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì Ax // By nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.
Lại có: ^ABy′ và ^BAx là hai góc so le trong.
Do đó, ^ABy′ = ^BAx = 50o.
Câu 6:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì ^ABy′ và ^ABM là hai góc kề bù nên:
^ABy′ + ^ABM = 180o
Thay số: 50o + ^ABM = 180o
^ABM = 180o – 50o
^ABM = 130o.
Câu 7:
21/07/2024Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Euclid?
 Xem đáp án
Xem đáp án
Lời giải:
Phát biểu diễn đạt đúng nội dung tiên đề Euclid là phát biểu b và phát biểu d.
Câu 8:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải:
Theo đề bài ra ta có:
^NMA=^MAB, mà hai góc này ở vị trí so le trong, suy ra MN // xx;
^PMy=^MBx′, mà hai góc này ở vị trí đồng vị, suy ra MP // xx’
Theo tiên đề Euclid, qu điểm M chỉ có một đường thẳng song song với xx’. Mà MN và NP cùng song song với xx’ nên MN vag MP trùng nhau.
Do đó, ba điểm M, N, P thẳng hàng.
Câu 9:
22/07/2024Vẽ lại Hình 3.22 vào vở.
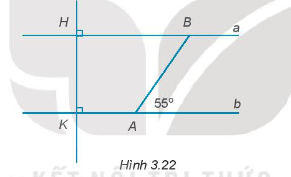
Giải thích tại sao a // b.
 Xem đáp án
Xem đáp án
Lời giải:
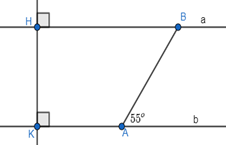
Vì HK vuông góc với a tại H; HK vuông góc với b tại K nên a // b (quan hệ từ vuông góc đến song song).
Câu 10:
19/07/2024Tính số đo góc ABH.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì a // b nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.
Lại có: ^ABH và ^BAb là hai góc so le trong.
Do đó, ^ABH = ^BAb = 55o.
Câu 11:
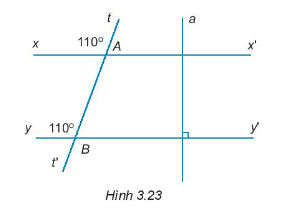
17/07/2024Vẽ lại Hình 3.23 vào vở. Giải thích tại sao
xx’ // yy’.
 Xem đáp án
Xem đáp án
Lời giải:
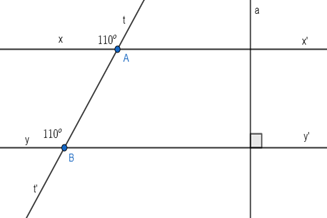
Ta có: ^tAx = 110o và ^yBt = 110o nên ^tAx = ^yBt = 110o. Mà hai góc này ở vị trí đồng vị. Do đó, xx’ song song với yy’.
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Câu 13:
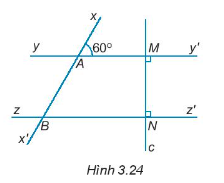
23/07/2024Cho Hình 3.24.
Giải thích tại sao yy’ // zz’.
 Xem đáp án
Xem đáp án
Lời giải:
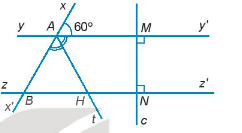
Theo hình vẽ ta có:
MN⊥yy’ và MN ⊥ zz’ nên yy’ // zz’.
Câu 14:
17/07/2024Tính số đo góc ABz.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có:
^xAy′ và ^ABz′ là hai góc đồng vị, mà yy’ // zz’ nên ^xAy′ = ^ABz′ = 60o.
Lại có ^ABz′ và ^ABz là hai góc kề bù.
Do đó, ^ABz′ + ^ABz = 180o.
Thay số: 60o + ^ABz = 180o.
^ABz = 180o – 60o
^ABz = 120o.
Câu 15:
22/07/2024Vẽ tia phân giác At của góc MAB, tia At cắt đường thẳng zz’ tại H. Tính số đo góc AHN.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì yy’ // zz’ mà hai góc ^ABz và ^MAB là hai góc so le trong nên ^ABz = ^MAB = 120o.
Vì At là tia phân giác của góc ^MAB nên ^HAM=^HAB=^MAB2=120∘2=60∘
Vì yy’ // xx’ và ^HAM; ^AHB là hai góc so le trong nên ^HAM = ^AHB = 60o.
Lại có: ^AHB và ^AHN là hai góc kề bù nên ^AHB+ ^AHN = 180o.
Thay số: 60o + ^AHN = 180o
^AHN = 180o – 60o
^AHN = 120o.
Câu 16:
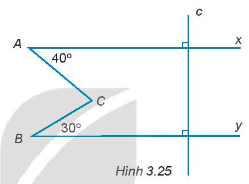
17/07/2024Cho Hình 3.25.
Giải thích tại sao Ax // By.
 Xem đáp án
Xem đáp án
Lời giải:
Vì Ax ⊥c; By ⊥ c nên Ax // By.
Câu 17:
22/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
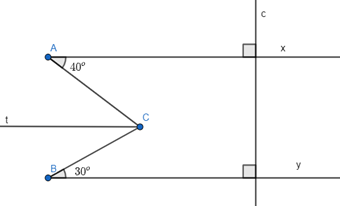
Kẻ Ct song song với Ax nên Ct cũng song song với By.
Vì Ct // Ax và ^xAC và ^ACt là hai góc so le trong nên ^xAC = ^ACt = 40o.
Vì Ct // By và ^BCt và ^yBC là hai góc so le trong nên ^BCt = ^yBC = 30o.
Lại có: ^ABC = ^ACt + ^BCt = 40o + 30o = 70o.
Vậy ^ABC = 70o.
Câu 18:
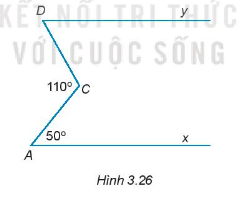
17/07/2024Cho Hình 3.26, biết Ax // Dy.
^xAC=50∘;^ACD=110∘. Tính số đo ^CDy.
 Xem đáp án
Xem đáp án
Lời giải:
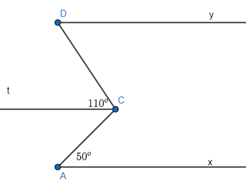
Kẻ tia Ct song song với Ax nên Ct song song với Dy (do Ax // Dy)
Vì Ax // Ct và ^CAx và ^ACt là hai góc so le trong nên ^CAx = ^ACt = 50o.
Ta lại có:
^ACt + ^tCD = 110o
50o + ^tCD = 110o
^tCD =110o – 50o
^tCD = 60o
Vì Ct // By và ^tCD và ^CDy là hai góc so le trong nên ^tCD = ^CDy = 60o.
Vậy ^CDy = 60o.
