Giải SBT Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song
-
40 lượt thi
-
8 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
29/06/2024Cho đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?
A. 0.
B. 1.
C. 2.
D. Vô số.
Xem đáp án
Đáp án đúng là: B
Theo hệ quả của định lí về tính chất của hai mặt phẳng song song: Nếu đường thẳng a song song với mặt phẳng (P) thì có duy nhất một mặt phẳng chứa a và song song với (P).
Câu 2:
23/07/2024Cho mặt phẳng (P) song song với mặt phẳng (Q). Khẳng định nào sau đây là đúng?
A. Mọi đường thẳng nằm trong (P) đều song song với mọi đường thẳng nằm trong (Q).
B. (P) song song với mọi đường thẳng nằm trong (Q).
C. Nếu mặt phẳng (R) song song với mặt phẳng (P) thì mặt phẳng (R) song song với mặt phẳng (Q).
D. Nếu đường thẳng a song song với mặt phẳng (Q) thì đường thẳng a song song với mặt phẳng (P).
Xem đáp án
Đáp án đúng là: B
Xét từng đáp án:
+ Đáp án A sai vì chúng có thể chéo nhau.
+ Đáp án B đúng.
+ Đáp án C sai vì mặt phẳng (R) có thể trùng với mặt phẳng (Q).
+ Đáp án D sai vì đường thẳng a có thể nằm trong mặt phẳng (P).
Câu 3:
17/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm các cạnh AB, CD, SA. Khẳng định nào sau đây là đúng?
A. (SBN) // (DAP).
B. (SBC) // (MPD).
C. (SBN) // (PMD).
D. (SDN) // (MAP).
Xem đáp án
Đáp án đúng là: C
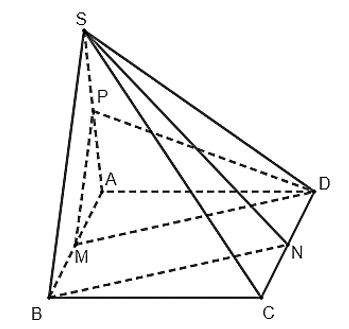
+ Ta có, P ∈ SA nên mặt phẳng (DAP) chính là mặt phẳng (SAD).
Mà hai mặt phẳng (SAD) và (SBN) có điểm chung là S nên chúng không thể song song.
Vậy hai mặt phẳng (SBN) và (DAP) không song song với nhau.
Do đó, đáp án A sai.
+ Trong mặt phẳng (ABCD), hai đường thẳng MD và BC cắt nhau.
Vậy hai mặt phẳng (SBC) và (MPD) không thể song song.
Do đó, đáp án B sai.
+ Mặt phẳng (MAP) chính là mặt phẳng (SAB).
Hai mặt phẳng (SAB) và (SDN) có điểm chung là S.
Vậy hai mặt phẳng (MAP) và (SAB) không thể song song.
Do đó, đáp án D sai. Vậy đáp án C đúng. Ta chứng minh như sau:
+ Vì M, N lần lượt là trung điểm của AB, CD và AB = CD, AB // CD (do ABCD là hình bình hành) nên BM // ND và BM // ND. Do đó, BMDN là hình bình hành.
Suy ra MD // BN. Mà BN ⊂ (SBN) nên MD // (SBN).
Lại có MP là đường trung bình của tam giác SAB nên MP // SB.
Mà SB ⊂ (SBN) nên MP // (SBN).
Vì MD và MP cắt nhau trong mặt phẳng (MPD) nên (MPD) // (SBN).
Câu 4:
21/07/2024Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Khẳng định nào sau đây là đúng?
A. (ADF) // (BCE).
B. AD // (BEF).
C. (ABC) // (DEF).
D. EC // (ABD).
Xem đáp án
Đáp án đúng là: A
+ Ta có AF // BE (ABEF là hình bình hành), mà BE ⊂ (BCE) nên AF // (BCE).
Lại có AD // BC (ABCD là hình bình hành), mà BC ⊂ (BCE) nên AD // (BCE).
Mà AF và AD cắt nhau trong mặt phẳng (ADF) nên (ADF) // (BCE). Vậy đáp án A đúng.
+ Vì AD ∩ (BEF) = A nên đáp án B sai.
+ Vì (ABC) ∩ (DEF) = CD nên đáp án C sai.
+ Vì EC ∩ (ABD) = C nên đáp án D sai.
Câu 5:
22/07/2024Cho a, b là hai đường thẳng phân biệt cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A', B', C'. Khẳng định nào sau đây là sai?
A. .
B. .
C. .
D. .
Xem đáp án
Đáp án đúng là: D
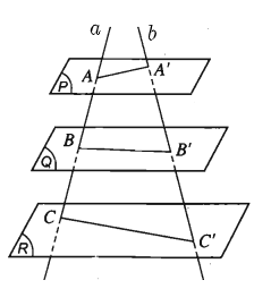
Theo định lí Thalès trong không gian, ta có: . (đáp án A đúng)
Suy ra . (đáp án B đúng)
Từ suy ra. (đáp án C đúng)
Vậy đáp án D sai.
Câu 6:
13/07/2024Trong mặt phẳng (P) cho tam giác ABC. Qua A, B, C lần lượt vẽ các tia Ax, By, Cz đôi một song song với nhau và không nằm trong mặt phẳng (P). Trên các tia Ax, By, Cz lần lượt lấy các điểm A', B', C' sao cho AA' = BB' = CC'. Chứng minh rằng (ABC) // (A'B'C').
Xem đáp án
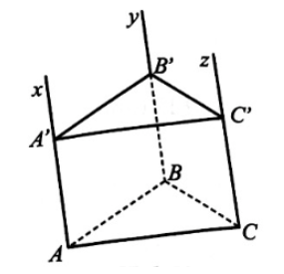
Vì AA' // BB' (Ax // By) và AA' = BB nên AA'B'B là hình bình hành.
Suy ra A'B' // AB. Mà AB ⊂ (ABC) nên A'B' // (ABC).
Tương tự ta chứng minh được B'C' // (ABC).
Mà A'B' và B'C' là hai đường thẳng cắt nhau trong mặt phẳng (A'B'C').
Từ đó, suy ra (ABC) // (A'B'C').
Câu 7:
18/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD. Gọi M là trọng tâm của tam giác SAD, N là điểm thuộc đoạn thẳng AC sao cho AN = AC, P là điểm thuộc đoạn thẳng CD sao cho DP = DC. Chứng minh rằng (MNP) // (SBC).
Xem đáp án
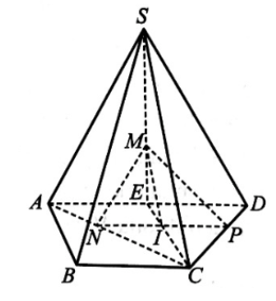
Gọi E là trung điểm của AD và I là giao điểm của NP và EC.
Ta có nên NP // AD.
Do AD // BC (ABCD là hình thang có AD là đáy) nên NP // BC.
Mà BC ⊂ (SBC). Suy ra NP // (SBC). (1)
Vì NP // AD nên ta có .
Do M là trọng tâm của tam giác SAD và E trung điểm của đoạn AD nên M ∈ SE và .
Như vậy nên MI // SC.
Mà SC ⊂ (SBC). Suy ra MI // (SBC). (2)
Lại có MI và NP là hai đường thẳng cắt nhau tại I trong mặt phẳng (MNP). (3)
Từ (1), (2) và (3) suy ra (MNP) // (SBC).
Câu 8:
15/07/2024Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên các đường chéo AC, BF lần lượt lấy các điểm M, N sao cho . Qua M vẽ đường thẳng song song với AB cắt AD tại M', qua N vẽ đường thẳng song song với AB cắt AF tại N'.
a) Chứng minh rằng (MNN') // (CDE).
b) Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Mặt phẳng (P) cắt đường thẳng EF tại I. Tính , biết .
Xem đáp án
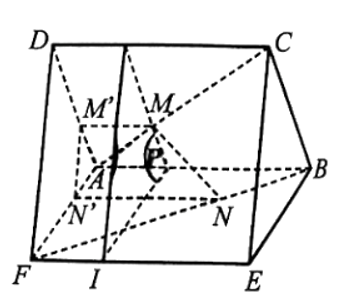
a) Ta có MM' // AB và NN' // AB (theo đề bài) nên MM' // NN'.
Suy ra M, M', N', N cùng thuộc một mặt phẳng. (1)
Ta có CD // AB (do ABCD là hình bình hành) và EF // AB (do ABEF là hình bình hành) nên CD // EF, suy ra C, D, F, E cùng thuộc một mặt phẳng.
Do AB // CD nên MM' // CD, mà CD ⊂ (CDE), suy ra MM' // (CDE). (2)
Theo định lí Thalés trong tam giác ACD, ta có (MM' // CD).
Tương tự, trong tam giác AFB có (NN' // AB).
Mà (theo đề bài). Do đó, , từ đó suy ra M'N' // DF.
Mà DF ⊂ (CDE) (do C, D, F, E cùng thuộc một mặt phẳng) nên M'N' // (CDE). (3)
Từ (2) và (3) suy ra (MM'N') // (CDE). (4)
Từ (1) và (4) suy ra (MNN') // (CDE).
b) Ta có AF // BE và AD // BC, từ đó suy ra (ADF) // (BCE).
Khi đó đường thẳng AC cắt ba mặt phẳng song song (ADF), (P), (BCE) lần lượt tại A, M, C; đường thẳng FE cũng cắt ba mặt phẳng trên theo thứ tự tại F, I, E.
Áp dụng định lí Thalés trong không gian, ta có: .
Suy ra . Mà nên .