Bài tập: Đường thẳng đi qua hai điểm chọn lọc, có đáp án
-
241 lượt thi
-
10 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho hai đường thẳng a, b. Khi đó a, b có thể:
Xem đáp án
Đáp án là D
Hai đường thẳng a, b bất kỳ có thể trùng nhau, song song hoặc cắt nhau.
Câu 2:
22/07/2024Chọn câu đúng:
Xem đáp án
Đáp án là B
• Đáp án A: Qua hai điểm phân biệt có một và chỉ một đường thẳng nên A sai.
• Đáp án B: Có vô số điểm thuộc một đường thẳng nên B đúng.
• Đáp án C: Hai đường thẳng phân biệt thì có thể song song hoặc cắt nhau nên C sai.
• Đáp án D: Trong ba điểm thẳng hàng thì chỉ có một điểm nằm giữa hai điểm còn lại nên D sai.
Câu 3:
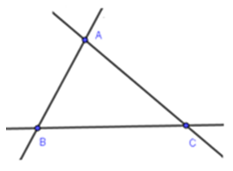
22/07/2024Cho ba điểm A; B; C không thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được những đường thẳng nào?
Xem đáp án
Đáp án là A
Các đường thẳng trong hình là: AB, BC, CA
Câu 4:
22/07/2024Cho 5 điểm A; B; C; D; E trong đó không có ba điểm nào thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng?
Xem đáp án
Đáp án là B
Các đường thẳng là: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE
Vậy có tất cả 10 đường thẳng cần tìm.
Câu 5:
22/07/2024Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
Xem đáp án
Đáp án là C
Ba đường thẳng đôi một không có giao điểm nghĩa là:
• a, b không có giao điểm hay a song song b.
• b, c không có giao điểm hay b song song c.
• a, c không có giao điểm hay a song song c.
Vậy ba đường thẳng đôi một song song.
Câu 6:
22/07/2024Cho bốn điểm M, N, P ,Q trong đó ba điểm M, N, P thẳng hàng và điểm Q nằm ngoài đường thẳng trên. Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng phân biệt?
Xem đáp án
Đáp án là B
Vì ba điểm M, N, P thẳng hàng nên qua hai điểm bất kì trong ba điểm trên ta đều nhận được một đường thẳng. Vậy từ ba điểm trên ta được một đường thẳng.
Các đường thẳng còn lại là: QM, QN, QP
Vậy có tất cả 4 đường thẳng phân biệt
Câu 7:
22/07/2024Cho ba điểm A, B, C không thẳng hàng. Ta nói gì về hai đường thẳng AB và AC
Xem đáp án
Đáp án là C
Vì A, B, C không thẳng hàng nên AB và AC phân biệt
Mà AB và AC có điểm chung duy nhất là A nên hai đường thẳng AB và AC cắt nhau
Câu 8:
22/07/2024Trong các khẳng định sau, khẳng định đúng là:
Xem đáp án
Đáp án là A
Có một và chỉ một đường thẳng đi qua hai điểm ( phân biệt) cho trước Đáp án A đúng
Ba điểm phân biệt có thể thẳng hàng hoặc không. Trong trường hợp ba điểm phân biệt thẳng hàng thì ta chỉ xác định được duy nhất một đường thẳng đi qua ba điểm phân biệt đó. Do đó, đáp án B sai
Tương tự, nếu bốn điểm phân biệt đó không thẳng hàng thì ta mới xác định được sáu đường thẳng đi qua bốn điểm phân biệt đó. Nếu trong bốn điểm phân biệt đó, có ba điểm thẳng hàng ta chỉ xác định được 4 đường thẳng, hoặc cả 4 điểm phân biệt đó đều thẳng hàng ta chỉ xác định được 1 đường thẳng. Do đó, đáp án C sai
Ba đường thẳng phân biệt có thể song song hoặc cắt nhau. Nếu ba đường thẳng đó đôi một cắt nhau thì ta có ba giao điểm. Nếu trong ba đường thẳng phân biệt đó, có hai đường thẳng song song với nhau, đường thẳng thứ ba cắt 2 đường thẳng còn lại thì ta có 2 giao điểm. Vậy đáp án D sai
Câu 9:
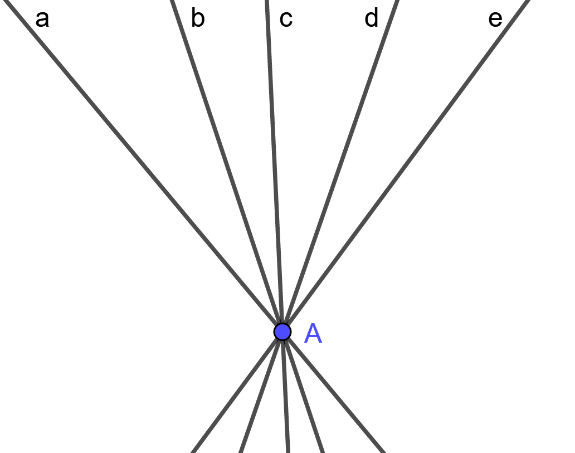
22/07/2024Cho năm đường thẳng cắt nhau từng đôi một cho ít nhất mấy giao điểm
Xem đáp án
Đáp án là A
Cho 5 đường thẳng cắt nhau từng đôi một, trường hợp cho ít giao điểm nhất là cả năm đường thẳng đều đi qua một điểm
5 đường thẳng a, b, c, d, e cắt nhau tại điểm A
Câu 10:
22/07/2024Cho ba đường thẳng cắt nhau từng đôi một cho nhiều nhất mấy giao điểm
Xem đáp án
Đáp án là C
Ba đường thẳng cắt nhau từng đôi một cho ta nhiều nhất ba giao điểm