Nội dung bài viết

    Xem thêm

    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x

    Với giải bài 38 trang 56 - 57 sgk Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 1,815 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Luyện tập trang 56, 57

    Video Giải Bài 38 trang 56-57 SGK Toán 9 Tập 2

    Bài 38 trang 56-57 SGK Toán 9 Tập 2: Giải các phương trình:

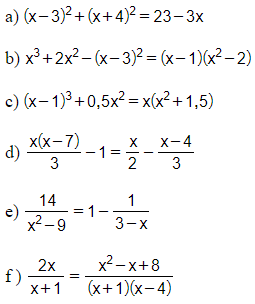
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Lời giải:

    a) 

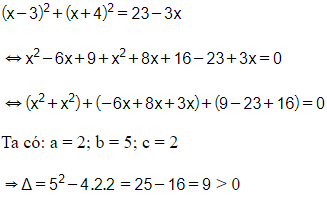
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Phương trình có hai nghiệm phân biệt

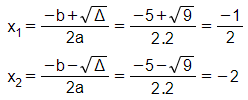
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Vậy phương trình có tập nghiệm S=−2;−12

    b)  x3 + 2x2 – (x – 3)2 = (x – 1)(x2 – 2)

    ⇔ x3 + 2x2 – (x2 – 6x + 9) = x3 – x2 – 2x + 2

    ⇔ x3 + 2x2 – x2 + 6x – 9 – x3 + x2 + 2x – 2 = 0

    ⇔ 2x2 + 8x – 11 = 0.

    Có a = 2; b = 8; c = -11 ⇒ Δ’ = 42 – 2.(-11) = 38 > 0

    ⇒ Phương trình có hai nghiệm phân biệt

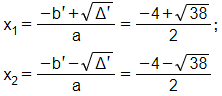
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Vậy phương trình có tập nghiệm S=−4−382;−4+382

    c) (x – 1)3 + 0,5x2 = x(x2 + 1,5)

    ⇔ x3 - 3x2 + 3x – 1 + 0,5x2 = x3 + 1,5x

    ⇔ x3 + 1,5x – x3 + 3x2 – 3x + 1 – 0,5x2 = 0

    ⇔ 2,5x2 – 1,5x + 1 = 0

    Có a = 2,5; b = -1,5; c = 1

    ⇒ Δ = (-1,5)2 – 4.2,5.1 = -7,75 < 0

    Vậy phương trình vô nghiệm.

    d)

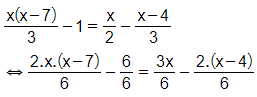
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    ⇔ 2x(x – 7) – 6 = 3x – 2(x – 4)

    ⇔ 2x2 – 14x – 6 = 3x – 2x + 8

    ⇔ 2x2 – 14x – 6 – 3x + 2x – 8 = 0

    ⇔ 2x2 – 15x – 14 = 0.

    Có a = 2; b = -15; c = -14

    ⇒ Δ = (-15)2 – 4.2.(-14) = 337 > 0

    ⇒ Phương trình có hai nghiệm phân biệt

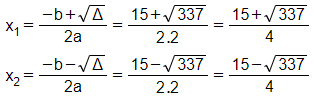
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Vậy tập nghiệm của phương trình S = 15−3374;15+3374

    e) Điều kiện: x≠±3

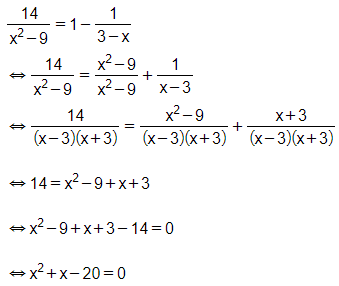
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Có a = 1; b = 1; c = -20

    ⇒ Δ = 12 – 4.1.(-20) = 81 > 0

    Phương trình có hai nghiệm phân biệt 

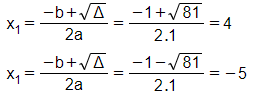
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Cả hai nghiệm đều thỏa mãn điều kiện xác định.

    Vậy phương trình có tập nghiệm S = {-5; 4}.

    f) Điều kiện: x≠−1;x≠4

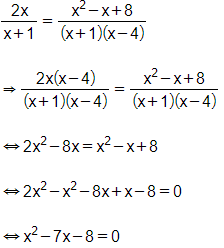
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Ta có: a= 1, b = -7, c = - 8

    ∆ = (-7)2 – 4.1. (- 8)= 81 > 0

    Phương trình có hai nghiệm phân biệt:

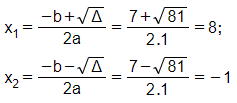
    Giải các phương trình: (x - 3)^2 + (x + 4)^2 = 23 - 3x (ảnh 1)

    Kết hợp với điều kiện đề bài t chỉ nhận x = 8 làm nghiệm

    Vậy phương trình đã cho có tập nghiệm S = {8}.

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Bài 37 trang 56 Toán 9 Tập 2: Giải phương trình trùng phương...

    Bài 39 trang 57 Toán 9 Tập 2: Giải phương trình bằng cách đưa về phương trình tích...

    Bài 40 trang 57 Toán 9 Tập 2: Giải phương trình bằng cách đặt ẩn phụ...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,815 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: