Câu hỏi:
09/01/2025 205Họ nguyên hàm của hàm số f(x) = tanx là
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
* Lời giải:
* Phương pháp giải:
áp dụng phương pháp biến đổi nguyên hàm để tính ra nguyên hàm của tanx
* Lý thuyết nắm thêm về nguyên hàm, tích phần
1. Phương pháp đổi biến số.
Định lý 1
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số x=φ(t) có đạo hàm liên tục trên đoạn [α;β] sao cho φ(α)=a;φ(b)=b và a≤φ(t)≤b với mọi t∈[α;β]. Khi đó:
b∫af(x)dx=β∫αf(φ(t))φ'
Từ định lý 1 ta rút ra các bước đổi biến số
1. Đặt , ta xác định đoạn sao cho và , ;
2. Biến đổi :
3. Tìm một nguyên hàm G(t) của g(t)
4. Tính
5. Kết luận
Định lý 2
Cho hàm số liên tục trên đoạn . Nếu hàm số có đạo hàm liên tục trên đoạn và với mọi sao cho liên tục trên đoạn thì
Từ định lý 2 ta rút ra các bước đổi biến số
1. Đặt ,
2. Biến đổi .
3. Tìm một nguyên hàm G(u) của g(u).
4. Tính .
5. Kết luận
2. Phương pháp tích phân từng phần.
Tương tự tính nguyên hàm từng phần, ta có định lý sau:
Nếu và là hai hàm số có đạo hàm liên tục trên đoạn thì
hay
Hay .
Một số cách đặt tích phân từng phần thường gặp với:
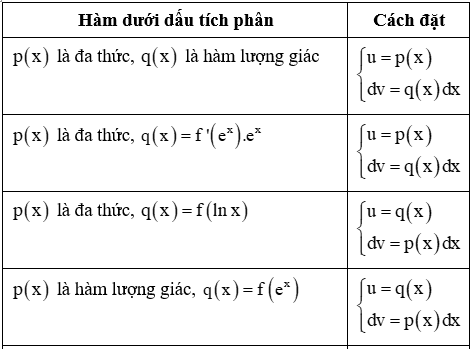
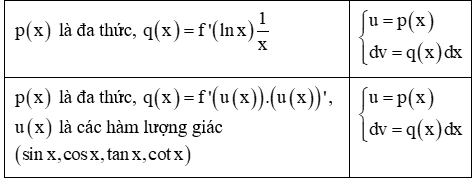
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài toán về các phương pháp tính tích phân (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho với a,b,c là các số nguyên dương và a/b tối giản. Giá trị của biểu thức a+b+c bằng
Câu 2:
Cho hàm số y = f(x) có đạo hàm liên tục đoạn [0;1] thỏa mãn f(0) = 0; f(1) = 1 và . Tích phân bằng
Câu 3:
Gọi (H) là hình phẳng giới hạn bởi parabol (P) và trục hoành. Các đường thẳng y = a; y = b;y =c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức bằng
Câu 4:
Một vật thể nằm giữa hai mặt phẳng x = -1; x = 1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x là một hình tròn có diện tích bằng 3π. Thể tích của vật thể là
Câu 6:
Cho hàm số y = f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt . Biết . Tích phân có giá trị lớn nhất bằng
Câu 7:
Thể tích khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi trục hoành và hai đường thẳng x = 0; x = 1 là
Câu 8:
Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1) = 1 và Tích phân bằng
Câu 11:
Cho với a,b,c là các số nguyên dương và tối giản. Giá trị biểu thức a+b+c bằng
Câu 12:
Cho hàm số y= f(x) xác định và liên tục trên R thỏa mãn . Tích phân bằng
Câu 15:
Cho với a,b là các số nguyên dương. Giá trị của biểu thức b-a bằng


