Câu hỏi:
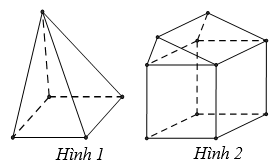
16/10/2024 461Hình nào dưới đây không phải là hình đa diện?
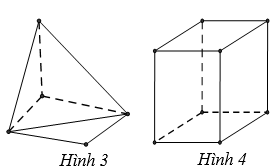
A. Hình 4
B. Hình 3
C. Hình 2
D. Hình 1
Trả lời:
Giải bởi Vietjack
Đáp án đúng: B.
*Phương pháp giải:
- Nắm kỹ về khái niệm, tính chất của hình đa diện: Nhận diện được hình, số đỉnh, số cạnh, số mặt,...của hình đa diện
*Lời giải:
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
a. Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b. Mỗi cạnh của đa giác là cạnh chung của đúng hai đa giác.
Mỗi đa giác như trên được gọi là một mặt của hình đa diện
Hình 3 không phải là hình đa diện. Vì không đảm bảo điều kiện: mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
*Lý thuyết nắm thêm về hình đa diện và khối đa diện
+) Hai đa diện bằng nhau: hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
+) Khối đa diện đều:
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
+) Thể tích khối đa diện:
- Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
+) Thể tích khối lăng trụ:
- Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
+) Thể tích khối chóp:
- Thể tích khối chóp có diện tích đáy B và chiều cao h là: V =
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khái niệm về khối đa diện – Toán 12
Trắc nghiệm Khái niệm về khối đa diện có đáp án (Thông hiểu)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho khối lăng trụ ABC.A'B'C'. Tỉ số thể tích giữa khối chóp A'.ABC và khối lăng trụ đó là
Câu 2:
I. Trắc nghiệm (5 điểm)
Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
Câu 3:
Cho khối chóp S.ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S.ABCD thành mấy khối tứ diện.
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a,
Câu 5:
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB. Mặt phẳng (AA'C'C) tạo với đáy một góc bằng 45°. Tính thể tích V của khối lăng trụ ABC.A'B'C'?
Câu 7:
Cho hình chóp S.ABC. Gọi (α) là mặt phẳng qua C và song song với AB. (α) cắt SA, SB lần lượt tại M, N. Tính tỉ số biết (α) chia khối chóp thành 2 phần có thể tích bằng nhau.
Câu 8:
Cho hình chóp S.ABC có SA ⊥ (ABC), đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB = a; SA = a.
Câu 10:
I. Tự luận ( 5 điểm)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng?
