Câu hỏi:
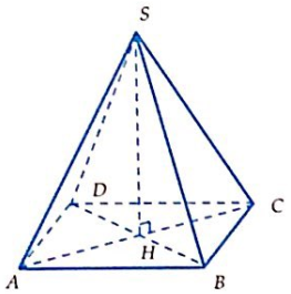
06/10/2024 280Hình chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích khối chóp đó bằng:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B
*Phương pháp giải:
- Áp dụng công thức tính thể tích hình chóp tứ giác đều để tính toán: mặt đáy của hình chóp tứ giác đều là hình vuông, các cạnh từ đỉnh chóp xuống 4 góc sẽ bằng nhau
*Lời giải:

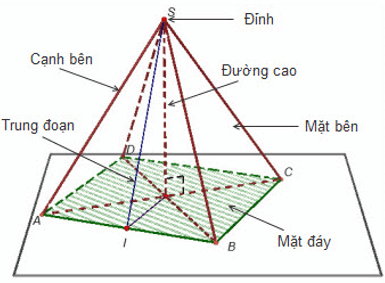
*Lý thuyết về hình chóp tứ giác đều
a) Hình chóp
- Đáy là một đa giác, các mặt bên là những tam giác có chung một đỉnh.
– Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao.
b) Hình chóp đều
Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
+ Chân đường cao của hình chóp đều trùng với tâm của đường tròn đi qua các đỉnh của mặt đáy.
+ Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
a) Diện tích xung quanh của hình chop đều
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (p: nửa chu vi đáy, d: trung đoạn)
b) Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + S (S: diện tích đáy)
c) Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:
V = 1/3S.h (S: diện tích đáy, h: chiều cao)
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài toán về thể tích khối chóp (có đáp án) – Toán 12
50 Bài tập Khối đa diện lồi và khối đa diện đều Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
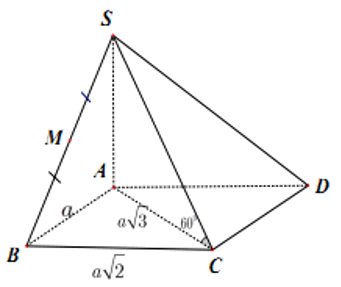
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a, SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
Câu 2:
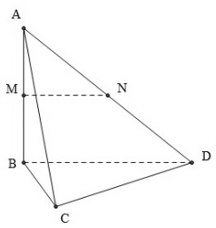
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = BC = 3a, BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
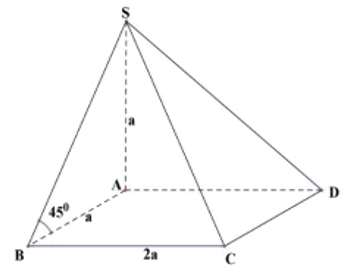
Câu 4:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng . Tính theo a thể tích khối chóp S.ABCD

Câu 5:
Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = a, DC = 2a. Tính diện tích S của tam giác ABC.
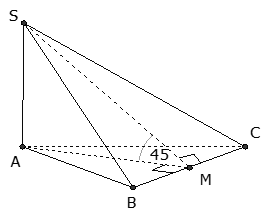
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a, cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng
Câu 7:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = a, khoảng cách từ A đến mặt (SCD) bằng a/3
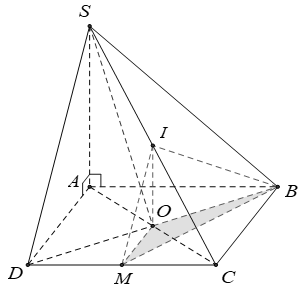
Câu 8:
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
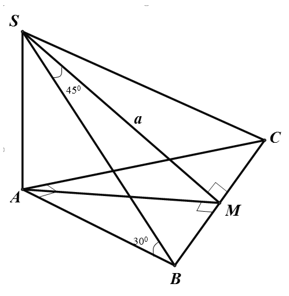
Câu 9:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC cân tại A. Cạnh bên SB lần lượt tạo với mặt phẳng đáy, mặt phẳng trung trực của BC các góc bằng 30° và 45°, khoảng cách từ S đến cạnh BC bằng a. Tính thể tích khối chóp S.ABC
Câu 10:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a; mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông cân tại S. Tính thể tích V của khối chóp S.ABC.
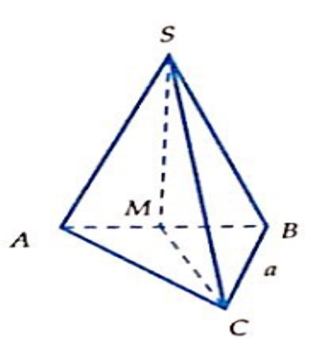
Câu 11:
Một hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích của khối chóp đó là:
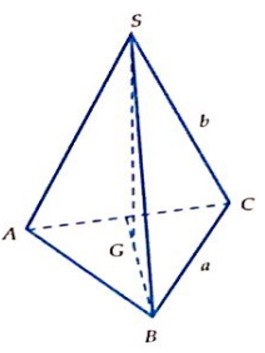
Câu 12:
Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60° AB = a. Khi đó thể tích của khối ABCC'B' bằng:
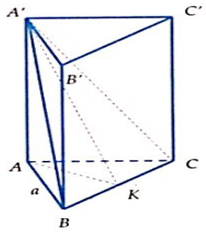
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết AB = a, AC = a, SB = a.

Câu 14:
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.
Câu 15:
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng a/4. Thể tích của hình chóp S.ABC là: