Câu hỏi:
13/07/2024 84
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc 90° (độ dốc 10% tương ứng với góc 9°). Giả sử có hai điểm A, B nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc AB dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc 90° (độ dốc 10% tương ứng với góc 9°). Giả sử có hai điểm A, B nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc AB dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
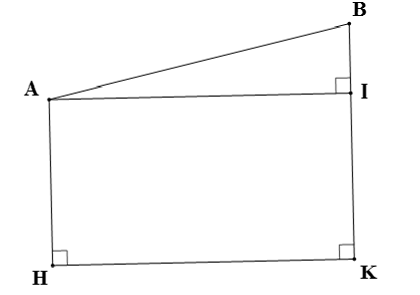
Bài toán được mô hình hóa như bài vẽ trên, với:
⦁ AB là chiều dài con dốc;
⦁ BI là độ cao của con dốc so với mặt phẳng nằm ngang;
⦁ AH và BK lần lượt là độ cao của điểm A và điểm B so với mặt nước biển.
Theo bài ra ta có: AH = 200 m, BK = 220 m, AB = 120 m và độ dốc của con dốc là góc được tạo bởi đường thẳng AB và đường thẳng AI (do AI là hình chiếu của AB trên mặt phẳng nằm ngang) và chính là số đo của
Dễ thấy AHKI là hình chữ nhật nên IK = AH = 200 m.
Suy ra BI = BK – IK = 220 – 200 = 20 (m).
Vì tam giác ABI vuông tại I nên ta có:
Vì độ dốc 100% tương ứng với góc 90°.
Suy ra góc 9,59° có độ dốc là
Vậy độ dốc của con dốc đó khoảng 10,66%.

Bài toán được mô hình hóa như bài vẽ trên, với:
⦁ AB là chiều dài con dốc;
⦁ BI là độ cao của con dốc so với mặt phẳng nằm ngang;
⦁ AH và BK lần lượt là độ cao của điểm A và điểm B so với mặt nước biển.
Theo bài ra ta có: AH = 200 m, BK = 220 m, AB = 120 m và độ dốc của con dốc là góc được tạo bởi đường thẳng AB và đường thẳng AI (do AI là hình chiếu của AB trên mặt phẳng nằm ngang) và chính là số đo của
Dễ thấy AHKI là hình chữ nhật nên IK = AH = 200 m.
Suy ra BI = BK – IK = 220 – 200 = 20 (m).
Vì tam giác ABI vuông tại I nên ta có:
Vì độ dốc 100% tương ứng với góc 90°.
Suy ra góc 9,59° có độ dốc là
Vậy độ dốc của con dốc đó khoảng 10,66%.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau:
a) [B, SA, D];
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau:
a) [B, SA, D];
Câu 3:
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]. Chứng minh rằng tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]. Chứng minh rằng tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.
Câu 4:
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình thoi cạnh a và AC = a.
a) Tính số đo của góc nhị diện [B, SA, C].
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình thoi cạnh a và AC = a.
a) Tính số đo của góc nhị diện [B, SA, C].
Câu 5:
c) Biết SA = a, tính số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD).
c) Biết SA = a, tính số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD).
Câu 6:
b) Chứng minh rằng AC ⊥ (SBD). Tính số đo của góc giữa đường thẳng SA và mặt phẳng (SBD).
b) Chứng minh rằng AC ⊥ (SBD). Tính số đo của góc giữa đường thẳng SA và mặt phẳng (SBD).
Câu 7:
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính đó, biết tam giác ABC có độ dài các cạnh là AB = AC = 30 cm và cm.
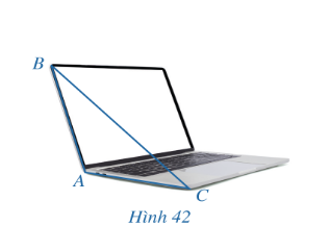
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính đó, biết tam giác ABC có độ dài các cạnh là AB = AC = 30 cm và cm.

Câu 8:
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (P), (Q) và cạnh của góc nhị diện là đường thẳng d.
Qua một điểm O trên đường thẳng d, ta kẻ hai tia Ox, Oy lần lượt thuộc hai nửa mặt phẳng (P), (Q) và cùng vuông góc với đường thẳng d. Góc xOy gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
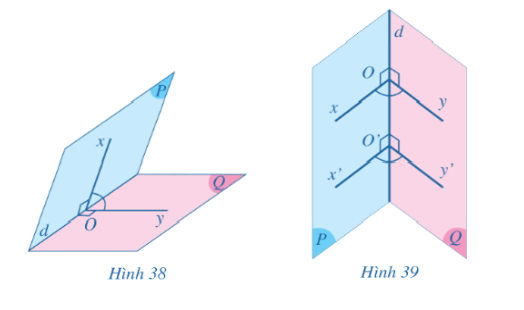
Giả sử góc x’O’y’ cũng là góc phẳng nhị diện của góc nhị diện đã cho với O’ khác O (Hình 39).
Hãy so sánh số đo của hai góc xOy và x’O’y’.
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (P), (Q) và cạnh của góc nhị diện là đường thẳng d.
Qua một điểm O trên đường thẳng d, ta kẻ hai tia Ox, Oy lần lượt thuộc hai nửa mặt phẳng (P), (Q) và cùng vuông góc với đường thẳng d. Góc xOy gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).

Giả sử góc x’O’y’ cũng là góc phẳng nhị diện của góc nhị diện đã cho với O’ khác O (Hình 39).
Hãy so sánh số đo của hai góc xOy và x’O’y’.
Câu 9:
Trong không gian cho hai mặt phẳng (α), (β) cắt nhau theo giao tuyến d. Hai mặt phẳng (α), (β) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?
Trong không gian cho hai mặt phẳng (α), (β) cắt nhau theo giao tuyến d. Hai mặt phẳng (α), (β) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?
Câu 10:
Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là trong cùng mặt phẳng. Lục giác ABCDEG nằm trong mặt phẳng đó có AB = GE = 2 m, BC = DE, Biết rằng khoảng cách từ C và D đến AG là 4 m, AG = 12 m, CD = 1 m. Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Câu 12:
c) Gọi M là trung điểm của cạnh AB. Tính số đo của góc nhị diện [M, SO, D].
c) Gọi M là trung điểm của cạnh AB. Tính số đo của góc nhị diện [M, SO, D].
Câu 13:
b) Góc giữa đường thẳng MO và hình chiếu của đường thẳng đó trên mặt phẳng (P) là góc nào.
b) Góc giữa đường thẳng MO và hình chiếu của đường thẳng đó trên mặt phẳng (P) là góc nào.
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai đường thẳng AC và BD cắt nhau tại O, SO ⊥ (ABCD), tam giác SAC là tam giác đều.
a) Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai đường thẳng AC và BD cắt nhau tại O, SO ⊥ (ABCD), tam giác SAC là tam giác đều.
a) Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD).
Câu 15:
Hình 32 biểu diễn một chiếc gậy dựa vào tường. Bạn Hoa nói góc nghiêng giữa chiếc gậy và mặt đất bằng 65°.
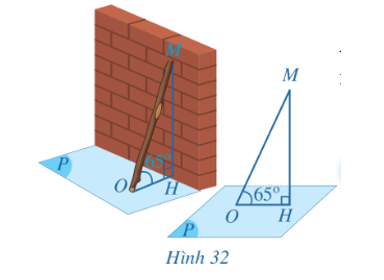
Góc nghiêng giữa chiếc gậy và mặt đất được hiểu như thế nào?
Hình 32 biểu diễn một chiếc gậy dựa vào tường. Bạn Hoa nói góc nghiêng giữa chiếc gậy và mặt đất bằng 65°.

Góc nghiêng giữa chiếc gậy và mặt đất được hiểu như thế nào?


