Câu hỏi:
21/07/2024 188Cho hình thang vuông ABCD có = 900, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 1370
B. 1360
C. 360
D. 1350
Trả lời:
Giải bởi Vietjack
Đáp án: D
Giải thích:
Lời giải
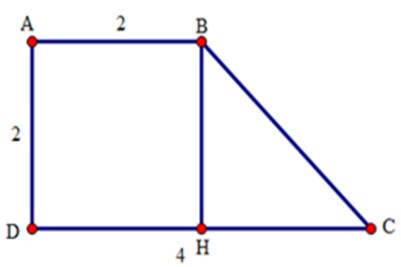
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có = 900 (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó = (1800 - ) : 2
= (1800 – 900) : 2 = 450
Xét hình thang ABCD có:
= 3600 – ()
= 3600 – (900 + 900 + 450) = 1350.
Vậy = 1350.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình thang vuông ABCD có = 900, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
Câu 3:
Cho hình thang ABCho hình thang ABCD có = 900, DC = BC = 2.AB, DC = 4cmCD có = 900, DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
Câu 5:
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
Chọn câu đúng nhất. Tứ giác ACMI là hình gì?
Câu 6:
Cho tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chọn khẳng định đúng
Câu 7:
Góc kề cạnh bên của hình thang có số đo là 1300. Góc kề còn lại của cạnh bên đó là
Câu 8:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
1. Chọn khẳng định đúng nhất?
Câu 9:
Góc kề cạnh bên của hình thang có số đo là 700. Góc kề còn lại của cạnh bên đó là
Câu 10:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
Chọn khẳng định đúng
