Câu hỏi:
20/07/2024 509
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.
a) Tính khoảng cách từ S đến mặt phẳng (ABC).
b) Tính khoảng cách từ M đến mặt phẳng (SAG).
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.
a) Tính khoảng cách từ S đến mặt phẳng (ABC).
b) Tính khoảng cách từ M đến mặt phẳng (SAG).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
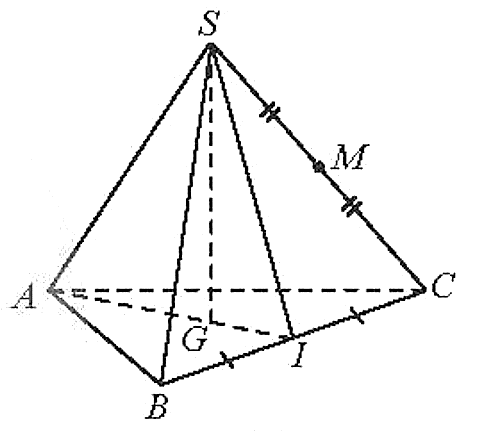
a) Do S.ABC là hình chóp tam giác đều nên SG ^ (ABC) hay d(S, (ABC))=SG.
Tam giác ABC là tam giác đều cạnh 3a nên
Tam giác SAG vuông tại G nên
Vậy d(S, (ABC)) = a.
b) Vì SC Ç (SAG) = S nên
Gọi I là trung điểm của BC.
Ta có: CB ^ AI và CB ^ SG
Þ CB ^ (SAG) và CB Ç (SAG) = I.
Do đó
Vậy

a) Do S.ABC là hình chóp tam giác đều nên SG ^ (ABC) hay d(S, (ABC))=SG.
Tam giác ABC là tam giác đều cạnh 3a nên
Tam giác SAG vuông tại G nên
Vậy d(S, (ABC)) = a.
b) Vì SC Ç (SAG) = S nên
Gọi I là trung điểm của BC.
Ta có: CB ^ AI và CB ^ SG
Þ CB ^ (SAG) và CB Ç (SAG) = I.
Do đó
Vậy
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA =
Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA =
Câu 2:
Một hình hộp chữ nhật có ba kích thước là 2 cm, 3 cm và 6 cm. Tính thể tích của khối tứ diện
Một hình hộp chữ nhật có ba kích thước là 2 cm, 3 cm và 6 cm. Tính thể tích của khối tứ diện
Câu 3:
Tính thể tích một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80 cm, đáy nhỏ có cạnh bằng 40 cm và cạnh bên bằng 80 cm.

Tính thể tích một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80 cm, đáy nhỏ có cạnh bằng 40 cm và cạnh bên bằng 80 cm.

Câu 4:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = , đáy ABCD là hình thang vuông tại A và B có AB = a, AD = 3a, BC = a. Tính thể tích khối chóp S.BCD theo a.
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = , đáy ABCD là hình thang vuông tại A và B có AB = a, AD = 3a, BC = a. Tính thể tích khối chóp S.BCD theo a.
Câu 5:
Cho hình chóp cụt tam giác đều có đường cao . Cho biết AB = 2a, . Gọi B1, C1 lần lượt là trung điểm của AB, AC. Tính thể tích của:
a) Khối chóp cụt đều .
b) Khối lăng trụ .
Cho hình chóp cụt tam giác đều có đường cao . Cho biết AB = 2a, . Gọi B1, C1 lần lượt là trung điểm của AB, AC. Tính thể tích của:
a) Khối chóp cụt đều .
b) Khối lăng trụ .
Câu 7:
Cho hình chóp S.ABC có tam giác vuông cân tại B, AC = , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60°. Tính theo a thể tích V của khối chóp S.ABC.
Cho hình chóp S.ABC có tam giác vuông cân tại B, AC = , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60°. Tính theo a thể tích V của khối chóp S.ABC.
Câu 8:
Cho hình lập phương cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C'. Tính khoảng cách giữa hai đường thẳng MN và B'D'.
Cho hình lập phương cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C'. Tính khoảng cách giữa hai đường thẳng MN và B'D'.


