Câu hỏi:
19/07/2024 130
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho.
a) Chứng minh ∆AMB = ∆CND.
b) Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng AM = 2MI.
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho.
a) Chứng minh ∆AMB = ∆CND.
b) Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng AM = 2MI.
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
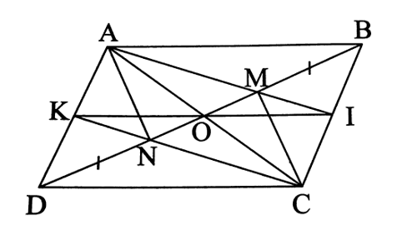
a) Vì ABCD là hình bình hành nên AB = CD và AB // CD.
Suy ra (hai góc so le trong).
Xét ∆AMB và ∆CND, ta có:
AB = CD (chứng minh trên);
(chứng minh trên);
BM = DN (giả thiết).
Suy ra ∆AMB = ∆CND (c.g.c).
b) Ta có ∆AMB = ∆CND (theo câu a), suy ra AM = CN (1)
Ta có: BM + MN = BN và DN + MN = DM; mà BM = DN, suy ra BN = DM.
Xét ∆ABN và ∆CDM, ta có:
AB = CD (chứng minh trên);
BN = DM (chứng minh trên)
Suy ra ∆ABN = ∆CDM (c.g.c), suy ra AN = CM (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
c) Vì AMCN là hình bình hành nên OA = OC.
∆ABC có OA = OC, suy ra BO là đường trung tuyến của ∆ABC.
ABCD là hình bình hành nên khi O là trung điểm của đường chéo AC thì O cũng là trung điểm của đường chéo BD, khi đó
Ta lại có: , suy ra
Do đó M là trọng tâm ∆ABC.
Khi đó Suy ra AM = 2MI.
d) Vì AMCN là hình bình hành nên AM // CN, mà M ∈ AI, N ∈ CK, nên AI // CK. (3)
Hơn nữa, AD // BC, K ∈ AD, I ∈ BC, nên AK // CI (4)
Từ (3), (4) suy ra AKCI là hình bình hành.
Mà O là trung điểm của AC, suy ra O cũng là trung điểm của KI hay I và K đối xứng nhau qua O.

a) Vì ABCD là hình bình hành nên AB = CD và AB // CD.
Suy ra (hai góc so le trong).
Xét ∆AMB và ∆CND, ta có:
AB = CD (chứng minh trên);
(chứng minh trên);
BM = DN (giả thiết).
Suy ra ∆AMB = ∆CND (c.g.c).
b) Ta có ∆AMB = ∆CND (theo câu a), suy ra AM = CN (1)
Ta có: BM + MN = BN và DN + MN = DM; mà BM = DN, suy ra BN = DM.
Xét ∆ABN và ∆CDM, ta có:
AB = CD (chứng minh trên);
BN = DM (chứng minh trên)
Suy ra ∆ABN = ∆CDM (c.g.c), suy ra AN = CM (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
c) Vì AMCN là hình bình hành nên OA = OC.
∆ABC có OA = OC, suy ra BO là đường trung tuyến của ∆ABC.
ABCD là hình bình hành nên khi O là trung điểm của đường chéo AC thì O cũng là trung điểm của đường chéo BD, khi đó
Ta lại có: , suy ra
Do đó M là trọng tâm ∆ABC.
Khi đó Suy ra AM = 2MI.
d) Vì AMCN là hình bình hành nên AM // CN, mà M ∈ AI, N ∈ CK, nên AI // CK. (3)
Hơn nữa, AD // BC, K ∈ AD, I ∈ BC, nên AK // CI (4)
Từ (3), (4) suy ra AKCI là hình bình hành.
Mà O là trung điểm của AC, suy ra O cũng là trung điểm của KI hay I và K đối xứng nhau qua O.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN. Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.
Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN. Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.
Câu 2:
Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) .
Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) .
Câu 3:
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Câu 4:
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Câu 5:
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Câu 6:
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Câu 7:
Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.
Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.











