Câu hỏi:
30/11/2024 351
Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) .
Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
*Lời giải
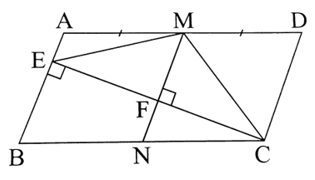
a) Ta có: MF ⊥ CE, AB ⊥ CE, suy ra MN // AB // CD.
Xét tứ giác MDCN ta có: MD // CN (do AD // BC; M ∈ AD, N ∈ BC) và MN // CD (chứng minh trên).
Do đó tứ giác MDCN là hình bình hành.
Mặt khác M là trung điểm của AD nên
Lại có AD = 2AB mà AB = CD (do ABCD là hình bình hành) nên
Do đó MD = CD.
Suy ra hình bình hành MDCN là hình thoi.
b) Xét tứ giác ADCE ta có AE // CD (theo câu a).
Do đó, tứ giác ADCE là hình thang với hai đáy AE và CD.
Xét hình thang ADCE có:
M là trung điểm AD (giả thiết);
AE // MF // CD (theo câu a).
Theo chứng minh ở Bài 5, trang 63, SBT Toán 8 Tập Một, ta có: F là trung điểm của CE.
Xét ∆EMC có MF là đường trung tuyến ứng với cạnh CE và MF ⊥ CE (giả thiết).
Do đó ∆EMC cân tại M.
c) Tứ giác MDCN là hình thoi nên (tính chất đường chéo của hình thoi).
Mà ∆EMC cân tại M nên
Ta có . (1)
Lại có (hai góc so le trong). (2)
Từ (1) và (2) suy ra .
*Phương pháp giải:
Nắm vững kiến thức và cách làm các bài toán về hình bình hành và hình thoi
* Một số lý thuyết và dạng bài thêm về hình bình hành - hình thoi:
1. Định nghĩa
Hình bình hành là tứ giác có các cặp cạnh đối song song
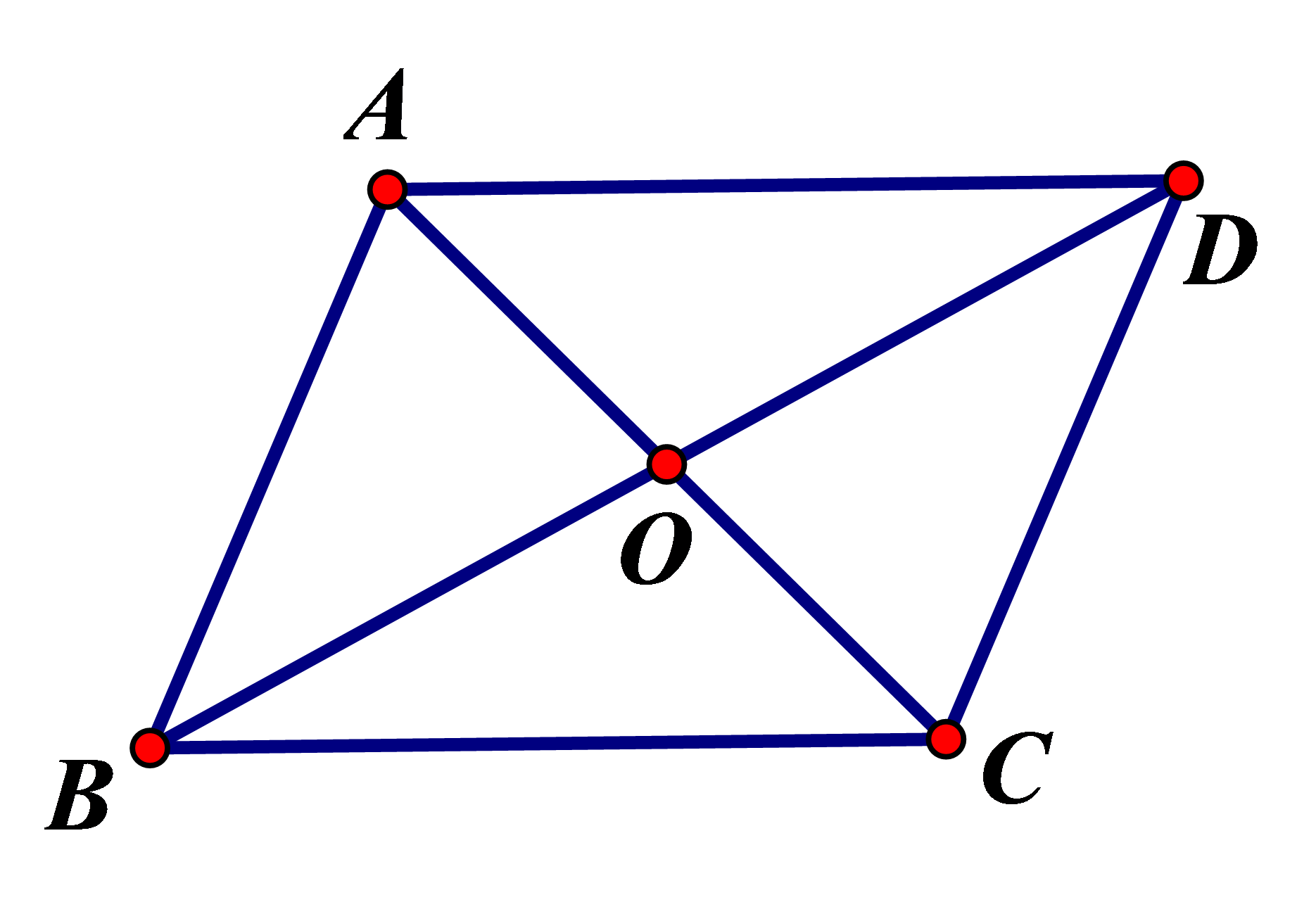
Tứ giác ABCD là hình bình hành
2. Tính chất: Trong hình bình hành
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Các dạng toán và phương pháp giải
Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa, các tính chất về cạnh, góc và đường chéo của hình bình hành.
Dạng 2. Chứng minh tứ giác là hình bình hành
Phương pháp giải: Áp dụng các dấu hiệu nhận biết của hình bình hành
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Dạng 3. Chứng minh ba điểm thẳng hàng, các đường thẳng đồng quy
Phương pháp giải: Vận dụng tính chất về đường chéo của hình bình hành: Hai đường chéo cắt nhau tại trung điểm mỗi đường.
HÌNH THOI:
1. Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
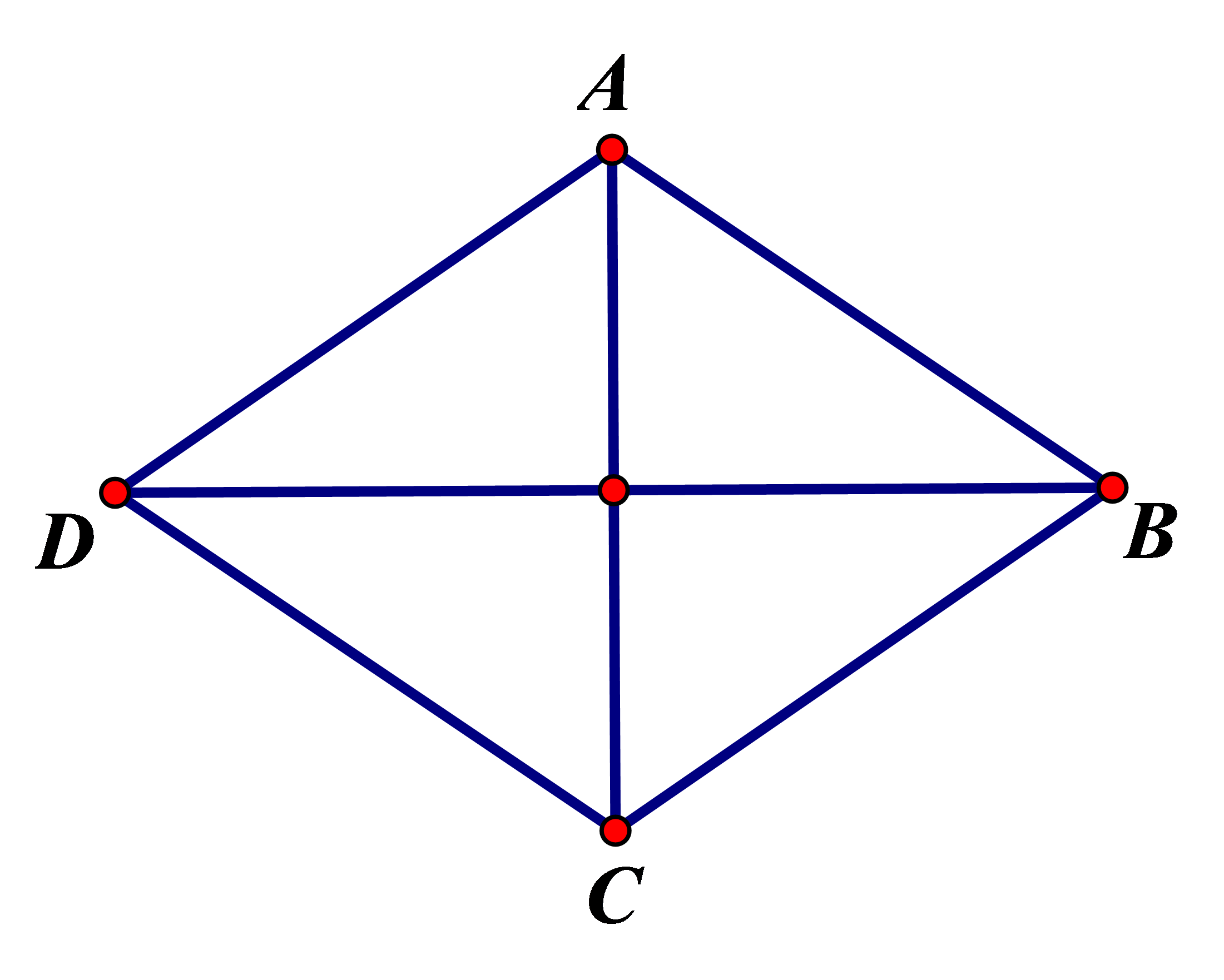
ABCD là hình thoi AB = BC = CD = DA.
Nhận xét: Hình thoi cũng là một hình bình hành.
2. Tính chất:
- Hình thoi có tất cả các tính chất của hình bình hành.
- Trong hình thoi:
a) Hai đường chéo vuông góc với nhau;
b) Hai đường chéo là đường phân giác của các góc ở đỉnh của hình thoi.
3. Dấu hiệu nhận biết:
a) Tứ giác có bốn cạnh bằng nhau là hình thoi;
b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi;
c) Hình bình hành có hai đường chéo vuông góc là hình thoi;
d) Hình bình hành có một đường chéo là đường phân giác của một góc ở đỉnh là hình thoi.
Các dạng bài tập và phương pháp giải
Dạng 1. Chứng minh tứ giác là hình thoi
Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi
Dạng 2. Vận dụng tính chất của hình thoi để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình thoi
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Toán 8 Bài 4 giải vở bài tập (Chân trời sáng tạo): Hình bình hành – Hình thoi

a) Ta có: MF ⊥ CE, AB ⊥ CE, suy ra MN // AB // CD.
Xét tứ giác MDCN ta có: MD // CN (do AD // BC; M ∈ AD, N ∈ BC) và MN // CD (chứng minh trên).
Do đó tứ giác MDCN là hình bình hành.
Mặt khác M là trung điểm của AD nên
Lại có AD = 2AB mà AB = CD (do ABCD là hình bình hành) nên
Do đó MD = CD.
Suy ra hình bình hành MDCN là hình thoi.
b) Xét tứ giác ADCE ta có AE // CD (theo câu a).
Do đó, tứ giác ADCE là hình thang với hai đáy AE và CD.
Xét hình thang ADCE có:
M là trung điểm AD (giả thiết);
AE // MF // CD (theo câu a).
Theo chứng minh ở Bài 5, trang 63, SBT Toán 8 Tập Một, ta có: F là trung điểm của CE.
Xét ∆EMC có MF là đường trung tuyến ứng với cạnh CE và MF ⊥ CE (giả thiết).
Do đó ∆EMC cân tại M.
c) Tứ giác MDCN là hình thoi nên (tính chất đường chéo của hình thoi).
Mà ∆EMC cân tại M nên
Ta có . (1)
Lại có (hai góc so le trong). (2)
Từ (1) và (2) suy ra .
*Phương pháp giải:
Nắm vững kiến thức và cách làm các bài toán về hình bình hành và hình thoi
* Một số lý thuyết và dạng bài thêm về hình bình hành - hình thoi:
1. Định nghĩa
Hình bình hành là tứ giác có các cặp cạnh đối song song

Tứ giác ABCD là hình bình hành
2. Tính chất: Trong hình bình hành
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Các dạng toán và phương pháp giải
Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa, các tính chất về cạnh, góc và đường chéo của hình bình hành.
Dạng 2. Chứng minh tứ giác là hình bình hành
Phương pháp giải: Áp dụng các dấu hiệu nhận biết của hình bình hành
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Dạng 3. Chứng minh ba điểm thẳng hàng, các đường thẳng đồng quy
Phương pháp giải: Vận dụng tính chất về đường chéo của hình bình hành: Hai đường chéo cắt nhau tại trung điểm mỗi đường.
HÌNH THOI:
1. Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

ABCD là hình thoi AB = BC = CD = DA.
Nhận xét: Hình thoi cũng là một hình bình hành.
2. Tính chất:
- Hình thoi có tất cả các tính chất của hình bình hành.
- Trong hình thoi:
a) Hai đường chéo vuông góc với nhau;
b) Hai đường chéo là đường phân giác của các góc ở đỉnh của hình thoi.
3. Dấu hiệu nhận biết:
a) Tứ giác có bốn cạnh bằng nhau là hình thoi;
b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi;
c) Hình bình hành có hai đường chéo vuông góc là hình thoi;
d) Hình bình hành có một đường chéo là đường phân giác của một góc ở đỉnh là hình thoi.
Các dạng bài tập và phương pháp giải
Dạng 1. Chứng minh tứ giác là hình thoi
Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi
Dạng 2. Vận dụng tính chất của hình thoi để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình thoi
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Toán 8 Bài 4 giải vở bài tập (Chân trời sáng tạo): Hình bình hành – Hình thoi
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN. Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.
Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN. Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.
Câu 2:
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Câu 3:
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Câu 4:
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho.
a) Chứng minh ∆AMB = ∆CND.
b) Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng AM = 2MI.
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho.
a) Chứng minh ∆AMB = ∆CND.
b) Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng AM = 2MI.
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.
Câu 5:
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Câu 6:
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Câu 7:
Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.
Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.











