Câu hỏi:
20/07/2024 240Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau
(I) ΔAME ~ ΔADC, tỉ số đồng dạng k1 =
(II) ΔCBA ~ ΔADC, tỉ số đồng dạng bằng k2 = 1
(III) ΔCNE ~ ΔADC, tỉ số đồng dạng k3 =
Chọn câu đúng.
A. (I) đúng, (II) và (III) sai
B. (I) và (II) đúng, (III) sai
C. Cả (I), (II), (III) đều đúng
D. Cả (I), (II), (III) đều sai.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: C
Giải thích:
Lời giải
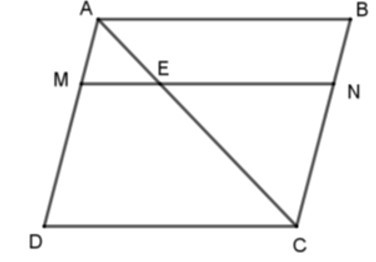
Vì ABCD là hình bình hành nên ME // DE và EN // AB.
+ ME // DC nên ΔAME ~ ΔADC,
tỉ số đồng dạng
+ Vì ABCD là hình bình hành
nên góc B = D; AD = BC; AB = DC
=> ΔCBA ~ ΔADC
ΔCBA ~ ΔADC, tỉ số đồng dạng bằng 1
+ EN // AB nên ΔCNE ~ ΔADC, do đó ΔCNE ~ ΔADC,
tỉ số đồng dạng
Vậy cả (I), (II), (III) đều đúng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:
Câu 2:
Cho tam giác ABC và hai điểm M, N lần lượt thuộc các cạnh BC, AC sao cho MN // AB. Chọn kết luận đúng
Câu 4:
Hãy chọn câu đúng. Tam giác ABC đồng dạng với tam giác MNP theo tỉ số , biết chu vi của tam giác ABC bằng 40 cm. Chu vi của tam giác MNP là:
Câu 5:
Cho ΔABC đồng dạng với ΔDEF và = 800, = 700, AC = 6cm. Số đo góc là:
Câu 7:
Cho tam giác ABC đồng dạng với tam giác A’B’C’. Hãy chọn phát biểu sai:
Câu 8:
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có = 800,
= 700, = 300; BC = 6cm. Nếu ΔABC đồng dạng với ΔDEF thì:
Câu 9:
Hình thang ABCD (AB // CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O.
Chọn khẳng định đúng.
Câu 10:
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là
Câu 11:
Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau
(I) ΔAME ~ ΔADC, tỉ số đồng dạng k1 =
(II) ΔCBA ~ ΔADC, tỉ số đồng dạng bằng k2 = 1
(III) ΔCNE ~ ΔADC, tỉ số đồng dạng k3 =
Số khẳng định đúng là:
Câu 12:
Hình thang ABCD (AB // CD) có AB = 9cm, CD = 12cm, hai đường chéo cắt nhau tại O. Chọn khẳng định không đúng.
Câu 13:
Hãy chọn câu đúng. Cho tam giác ABC có AB = AC = 5cm, BC = 4 cm đồng dạng với tam giác MNP theo tỉ số . Chu vi của tam giác MNP là:
Câu 14:
Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của tam giác A’B’C’ và ABC bằng











