Câu hỏi:
28/09/2024 187
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
A. 0.
B. 1.
C. 2.
D. Vô số.
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
A. 0.
B. 1.
C. 2.
D. Vô số.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Theo lí thuyết, cho hai đường thẳng chéo nhau, khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Vậy nếu hai đường thẳng a và b chéo nhau thì có duy nhất một mặt phẳng chứa a và song song với b.
*Lý thuyết liên quan
1. Đường thẳng song song với mặt phẳng
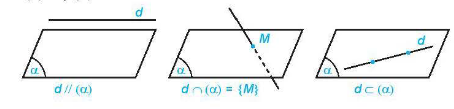
Cho đường thẳng d và mặt phẳng . Nếu d và không có điểm chung thì ta nói d song song với hay song song với d. Kí hiệu là hay .
*Nhận xét:
Nếu d và có một điểm chung duy nhất thì ta nói d và cắt nhau tại M. Kí hiệu hay .
Nếu d và có nhiều hơn 1 điểm chung thì ta nói d nằm trong hay chứa d. Kí hiệu hay .
2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng
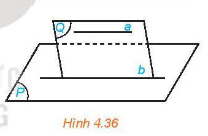
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì ta nói .
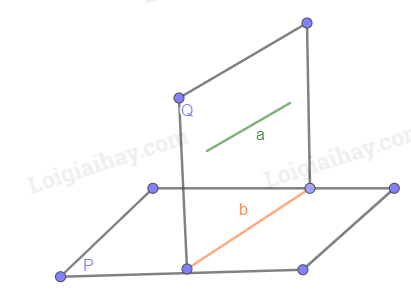
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.
Đáp án đúng là: B
Theo lí thuyết, cho hai đường thẳng chéo nhau, khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Vậy nếu hai đường thẳng a và b chéo nhau thì có duy nhất một mặt phẳng chứa a và song song với b.
*Lý thuyết liên quan
1. Đường thẳng song song với mặt phẳng
Cho đường thẳng d và mặt phẳng . Nếu d và không có điểm chung thì ta nói d song song với hay song song với d. Kí hiệu là hay .
*Nhận xét:
Nếu d và có một điểm chung duy nhất thì ta nói d và cắt nhau tại M. Kí hiệu hay .
Nếu d và có nhiều hơn 1 điểm chung thì ta nói d nằm trong hay chứa d. Kí hiệu hay .

2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì ta nói .

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.

CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của CD, SB.
a) Xác định giao tuyến của hai mặt phẳng (SAB) và (CDN).
b) Chứng minh rằng đường thẳng CN song song với mặt phẳng (SAM).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của CD, SB.
a) Xác định giao tuyến của hai mặt phẳng (SAB) và (CDN).
b) Chứng minh rằng đường thẳng CN song song với mặt phẳng (SAM).
Câu 2:
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ACD, điểm M nằm trên cạnh AB sao cho AM = 2MB. Đường thẳng MG song song với mặt phẳng:
A. (ACD).
B. (ABD).
C. (BCD).
D. (ABC).
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ACD, điểm M nằm trên cạnh AB sao cho AM = 2MB. Đường thẳng MG song song với mặt phẳng:
A. (ACD).
B. (ABD).
C. (BCD).
D. (ABC).
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CD, SA.
a) Chứng minh rằng SC song song với mặt phẳng (MNP).
b) Xác định giao tuyến của hai mặt phẳng (MNP) và (SCD).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CD, SA.
a) Chứng minh rằng SC song song với mặt phẳng (MNP).
b) Xác định giao tuyến của hai mặt phẳng (MNP) và (SCD).
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm chuyển động trên cạnh SC (M khác C), (P) là mặt phẳng chứa đường thẳng AM và song song với BD. Chứng minh rằng mặt phẳng (P) luôn đi qua một đường thẳng cố định khi điểm M chuyển động trên cạnh SC.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm chuyển động trên cạnh SC (M khác C), (P) là mặt phẳng chứa đường thẳng AM và song song với BD. Chứng minh rằng mặt phẳng (P) luôn đi qua một đường thẳng cố định khi điểm M chuyển động trên cạnh SC.
Câu 5:
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, BC, CD. Chứng minh rằng giao tuyến của hai mặt phẳng (APQ) và (CMN) song song với đường thẳng BD.
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, BC, CD. Chứng minh rằng giao tuyến của hai mặt phẳng (APQ) và (CMN) song song với đường thẳng BD.
Câu 6:
Trong các không gian hẹp, người ta thường thiết kế tủ đựng quần áo có cánh cửa trượt. Tủ này bao gồm khoang tủ, cánh cửa trượt và hai đường ray trượt cho mép trên và mép dưới cánh cửa (Hình 25). Biết rằng cánh cửa trượt có dạng hình chữ nhật và có thể kéo trượt bình thường, khi đó bạn Minh nói: “Đường ray trượt ở mép trên cửa song song với mặt đáy của tủ quần áo”. Em hãy cho biết phát biểu của bạn Minh đúng hay sai? Vì sao?

Trong các không gian hẹp, người ta thường thiết kế tủ đựng quần áo có cánh cửa trượt. Tủ này bao gồm khoang tủ, cánh cửa trượt và hai đường ray trượt cho mép trên và mép dưới cánh cửa (Hình 25). Biết rằng cánh cửa trượt có dạng hình chữ nhật và có thể kéo trượt bình thường, khi đó bạn Minh nói: “Đường ray trượt ở mép trên cửa song song với mặt đáy của tủ quần áo”. Em hãy cho biết phát biểu của bạn Minh đúng hay sai? Vì sao?

Câu 7:
Cho đường thẳng a song song với mặt phẳng (P). Khẳng định nào sau đây là sai?
A. Nếu có mặt phẳng (Q) chứa đường thẳng a và cắt (P) theo giao tuyến b thì b song song với a.
B. Trong mặt phẳng (P) có vô số đường thẳng chéo nhau với a.
C. Đường thẳng a không có điểm chung với mặt phẳng (P).
D. Trong mặt phẳng (P) có duy nhất một đường thẳng song song với a.
Cho đường thẳng a song song với mặt phẳng (P). Khẳng định nào sau đây là sai?
A. Nếu có mặt phẳng (Q) chứa đường thẳng a và cắt (P) theo giao tuyến b thì b song song với a.
B. Trong mặt phẳng (P) có vô số đường thẳng chéo nhau với a.
C. Đường thẳng a không có điểm chung với mặt phẳng (P).
D. Trong mặt phẳng (P) có duy nhất một đường thẳng song song với a.
Câu 8:
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt (P) theo giao tuyến b. Vị trí tương đối giữa a và b là:
A. Cắt nhau.
B. Trùng nhau.
C. Song song.
D. Chéo nhau.
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt (P) theo giao tuyến b. Vị trí tương đối giữa a và b là:
A. Cắt nhau.
B. Trùng nhau.
C. Song song.
D. Chéo nhau.


