Câu hỏi:
17/07/2024 221Cho A, B là hai điểm biểu diễn hình học số phức theo thứ tự z0, khác 0 và thỏa mãn đẳng thức . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. cân tại O.
B. Vuông cân tại O.
C. đều.
D. Vuông tại O.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Với ta có ![]()
![]()
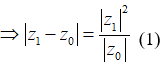
Với , ta có ![]()
![]()
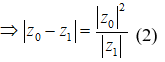
Từ (1), (2) ta có: 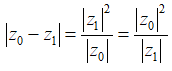
![]()
=> OA = OB = AB => OAB là tam giác đều.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho số phức z thỏa mãn |z - 3 - 4i| = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = - . Tính mô đun của số phức = M + mi
Câu 2:
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | - 3i| là đường thẳng có phương trình
Câu 4:
Cho số phức z thỏa mãn điều kiện (1+i) - 1 - 3i = 0. Tìm phần ảo của số phức w = 1 - zi +
Câu 5:
Xét các số phức z = a + bi(a,b) thỏa mãn điều kiện |z - 4 - 3i| = . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i + |z - 1 + i|| đạt giá trị lớn nhất.
Câu 8:
Cho số phức z = a + bi(trong đó a, b là các số thực) thỏa mãn 3z - (4+5i) = -17 + 11i. Tính ab
Câu 9:
Cho các số phức với 0. Tập hợp các điểm biểu diễn số phức w = là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là đường nào sau đây?
Câu 10:
Gọi là bốn nghiệm phức của phương trình - 8 = 0. Trên mặt phẳng tọa độ z gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.
Câu 12:
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + + 2| trên mặt phẳng tọa độ là một
Câu 13:
Cho số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
Câu 14:
Cho số phức z = a + bi(a,b ∈ℝ) thỏa mãn a + (b-1)i = . Giá trị nào dưới đây là mô đun của z?
Câu 15:
Cho số phức z = a + bi(a,b ) và xét hai số phức . Trong các khẳng định dưới đây, khẳng định nào đúng?


