Câu hỏi:
22/07/2024 141
b) Gọi I = MQ ∩ NP. Chứng minh rằng I luôn luôn thuộc một đường thẳng cố định khi M di động trên AD.
b) Gọi I = MQ ∩ NP. Chứng minh rằng I luôn luôn thuộc một đường thẳng cố định khi M di động trên AD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b) Gọi d là giao tuyến của (SAD) ∩ (SBC)
Ta có:
Mà S ∈ (SAD) ∩ (SBC) nên S ∈ d
Ta lại có:
Do đó I ∈ d
Vì vậy I thuộc đường thẳng d cố định đi qua S và song song với AD.
b) Gọi d là giao tuyến của (SAD) ∩ (SBC)
Ta có:
Mà S ∈ (SAD) ∩ (SBC) nên S ∈ d
Ta lại có:
Do đó I ∈ d
Vì vậy I thuộc đường thẳng d cố định đi qua S và song song với AD.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm hai đường chéo. Gọi M là trung điểm của SC.
a) Chứng minh đường thẳng OM song song với hai mặt phẳng (SAD) và (SBD).
b) Tìm giao tuyến của hai mặt phẳng (OMD) và (SAD).
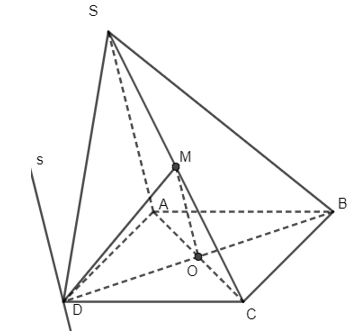
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm hai đường chéo. Gọi M là trung điểm của SC.
a) Chứng minh đường thẳng OM song song với hai mặt phẳng (SAD) và (SBD).
b) Tìm giao tuyến của hai mặt phẳng (OMD) và (SAD).

Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt N, P, Q.
a) MNPQ là hình gì?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt N, P, Q.
a) MNPQ là hình gì?
Câu 5:
Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và DB.
a) Chứng minh MNPQ là hình bình hành.
Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và DB.
a) Chứng minh MNPQ là hình bình hành.
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của CD, (P) là mặt phẳng qua M song song với SA và BC. Tìm giao tuyến của (P) với các mặt của hình chóp S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của CD, (P) là mặt phẳng qua M song song với SA và BC. Tìm giao tuyến của (P) với các mặt của hình chóp S.ABCD.
Câu 7:
Cho hai hình bình hành ABCD và ABEF không nằm trong cùn một mặt phẳng. Gọi O và O’ lần lượt là tâm của ABCD và ABEF.
a) Chứng minh đường thẳng OO’ song song với các mặt phẳng (CDEF), (ADF) và (BCE).
Câu 8:
Cho E và F lần lượt là trung điểm các cạnh AB và AC của tứ diện ABCD. Xác định vị trí tương đối của các đường thẳng BC, AD và EF với mặt phẳng (BCD).
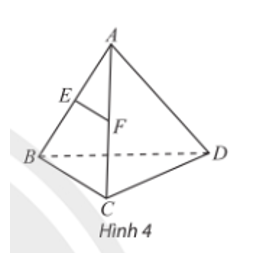
Cho E và F lần lượt là trung điểm các cạnh AB và AC của tứ diện ABCD. Xác định vị trí tương đối của các đường thẳng BC, AD và EF với mặt phẳng (BCD).

Câu 9:
b) Gọi M và N lần lượt là trung điểm của AF và BE. Chứng minh MN // (CDFE).
b) Gọi M và N lần lượt là trung điểm của AF và BE. Chứng minh MN // (CDFE).
Câu 10:
Cho đường thẳng a song song với mặt phẳng (P), mặt phẳng (Q) chứa a và cắt (P) theo giao tuyết b (Hình 10). Trong (Q), hai đường thẳng a, b có bao nhiêu điểm chung?
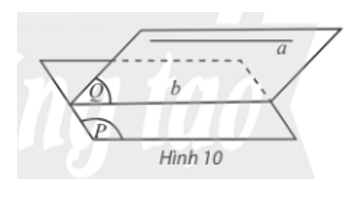
Cho đường thẳng a song song với mặt phẳng (P), mặt phẳng (Q) chứa a và cắt (P) theo giao tuyết b (Hình 10). Trong (Q), hai đường thẳng a, b có bao nhiêu điểm chung?

Câu 11:
Cho hình chóp S.ABC có ABCD là hình bình hành và M, N, E lần lượt là trung điểm của các đoạn thẳng AB, CD, SA (Hình 17). Chứng minh rằng:
a) MN song song với hai mặt phẳng (SBC) và (SAD);
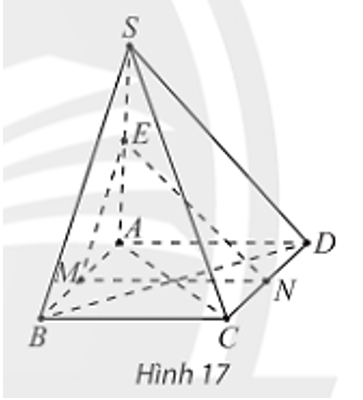
Cho hình chóp S.ABC có ABCD là hình bình hành và M, N, E lần lượt là trung điểm của các đoạn thẳng AB, CD, SA (Hình 17). Chứng minh rằng:
a) MN song song với hai mặt phẳng (SBC) và (SAD);

Câu 12:
Mô tả vị trí tương đối của các đường thẳng a, b, c, d, e với mặt phẳng (P) là mặt trước của tòa nhà (Hình 19).

Mô tả vị trí tương đối của các đường thẳng a, b, c, d, e với mặt phẳng (P) là mặt trước của tòa nhà (Hình 19).

Câu 14:
Cho hai hình bình hành ABCD và ABMN không đồng phẳng. Tìm số giao điểm của mặt phẳng (ABCD) lần lượt với các đường thẳng MN, MA và AC.
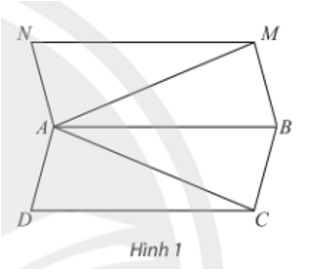
Cho hai hình bình hành ABCD và ABMN không đồng phẳng. Tìm số giao điểm của mặt phẳng (ABCD) lần lượt với các đường thẳng MN, MA và AC.

Câu 15:
b) Gọi (P’) là mặt phẳng chứa a và song song với b. Có nhận xét gì về mối liên hệ giữa b’ và (P’); (P) và (P’)?
b) Gọi (P’) là mặt phẳng chứa a và song song với b. Có nhận xét gì về mối liên hệ giữa b’ và (P’); (P) và (P’)?


