Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b) Gọi
Xét ΔAHD và ΔDKC:
AH = DK
AD = CD
ΔAHD = ΔDKC (c.g.c)
Ta có:
DH ⊥ CK
Mà SH ⊥ (ABCD) SH ⊥ CK
Vậy CK ⊥ (SDH).
b) Gọi
Xét ΔAHD và ΔDKC:
AH = DK
AD = CD
ΔAHD = ΔDKC (c.g.c)
Ta có:
DH ⊥ CK
Mà SH ⊥ (ABCD) SH ⊥ CK
Vậy CK ⊥ (SDH).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD).
b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD).
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông với AB là cạnh góc vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Cho M, N, P, Q lần lượt là trung điểm của SB, AB, CD, SC. Chứng minh rằng:
a) AB ⊥ (MNPQ);
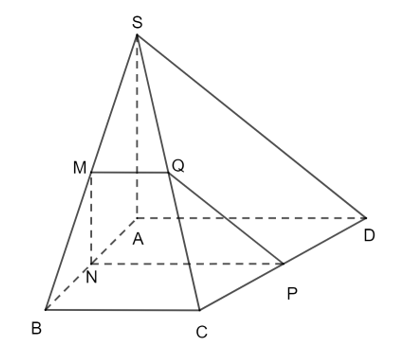
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông với AB là cạnh góc vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Cho M, N, P, Q lần lượt là trung điểm của SB, AB, CD, SC. Chứng minh rằng:
a) AB ⊥ (MNPQ);

Câu 3:
Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD.
a) Chứng minh CD ⊥ (SAD).
Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD.
a) Chứng minh CD ⊥ (SAD).
Câu 4:
Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:
a) AC ⊥ (SHK);
Câu 6:
Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m.
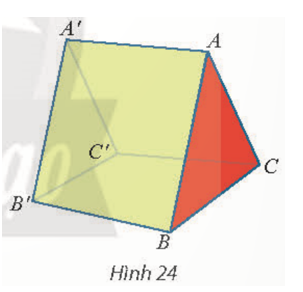
a) Tính góc giữa hai đường thẳng AA′ và BC; A′B′ và AC.
Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m.

a) Tính góc giữa hai đường thẳng AA′ và BC; A′B′ và AC.
Câu 7:
b) Tính diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB′CC′).
b) Tính diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB′CC′).
Câu 8:
Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC. Vẽ OH là đường cao của tam giác OBC. Chứng minh rằng:
a) OA ⊥ (A′B′C′);
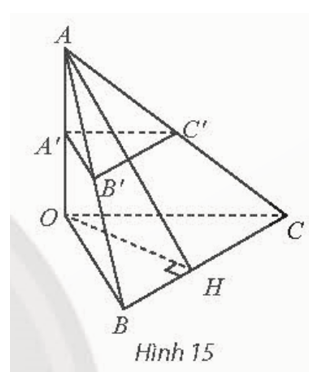
Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC. Vẽ OH là đường cao của tam giác OBC. Chứng minh rằng:
a) OA ⊥ (A′B′C′);

Câu 9:
Cho hình chóp S.ABC có SA = SB = SC = a, và . Gọi I là trung điểm cạnh AC. Chứng minh SI ⊥ (ABC).
Cho hình chóp S.ABC có SA = SB = SC = a, và . Gọi I là trung điểm cạnh AC. Chứng minh SI ⊥ (ABC).
Câu 10:
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Xác định hình chiếu vuông góc của điểm C, đường thẳng CD và tam giác SCD trên mặt phẳng (SAB).
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Xác định hình chiếu vuông góc của điểm C, đường thẳng CD và tam giác SCD trên mặt phẳng (SAB).
Câu 11:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng , có các cạnh bên đều bằng 2a.
a) Tính góc giữa SC và AB.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng , có các cạnh bên đều bằng 2a.
a) Tính góc giữa SC và AB.
Câu 12:
Cho hình chóp S.ABCD có đáy là hình vuông, O là giao điểm của AC và BD, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần luợt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC, SD. Chứng minh rằng:
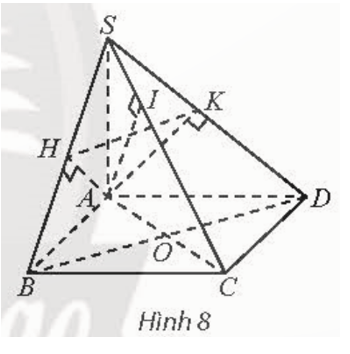
a) CB ⊥ (SAB) và CD ⊥ (SAD);
Câu 13:
b) Có nhận xét gì về tam giác DEF? Từ đó suy ra góc giữa d và c.
b) Có nhận xét gì về tam giác DEF? Từ đó suy ra góc giữa d và c.
Câu 14:
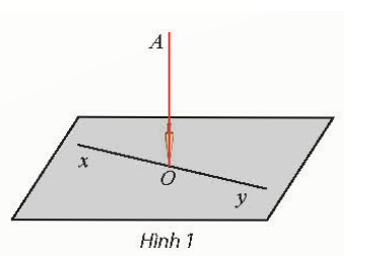
Thả một dây dọi AO chạm sàn nhà tại điểm O. Kẻ một đường thẳng xOy bất kì trên sàn nhà.
a) Dùng êke để kiểm tra xem AO có vuông góc với xOy không.
Thả một dây dọi AO chạm sàn nhà tại điểm O. Kẻ một đường thẳng xOy bất kì trên sàn nhà.
a) Dùng êke để kiểm tra xem AO có vuông góc với xOy không.

Câu 15:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Vẽ đường thẳng qua O và vuông góc với (ABC) tại H. Chứng minh AH ⊥ BC.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Vẽ đường thẳng qua O và vuông góc với (ABC) tại H. Chứng minh AH ⊥ BC.


