Nội dung bài viết

    Xem thêm

    Vẽ đồ thị của các hàm số y = x + 1 và y = -x + 3 trên cùng một mặt phẳng tọa độ

    Với giải bài 17 trang 51, 52 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 1,148 03/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Luyện tập: Đồ thị của hàm số bậc nhất

    Bài 17 trang 51, 52 Toán lớp 9 Tập 1:

    a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x + 3 trên cùng một mặt phẳng tọa độ.

    b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C.

    c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)

    Lời giải:

    a) - Với hàm số y = x + 1:

    Cho x = 0⇒ y = 1 ta được M (0; 1).

    Cho y = 0 => x + 1 = 0 ⇒ x = -1 ta được A (-1; 0).

    Nối MA ta được đồ thị hàm số y = x + 1.

    - Với hàm số y = -x + 3:

    Cho x = 0 ⇒ y = 3 ta được N (0; 3).

    Cho y = 0 ⇒ -x + 3 = 0 ⇒ x = 3 ta được B (3; 0).

    Nối NB ta được đồ thị hàm số y = -x + 3.

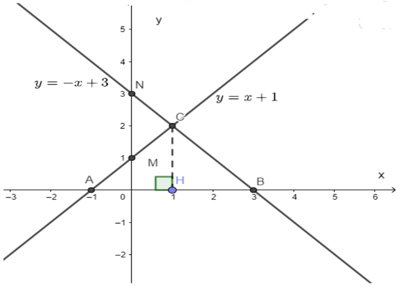
    Tài liệu VietJack

    b) Theo câu a ta có đồ thị hàm số y = x + 1 cắt trục Ox tại A (-1; 0)

    Theo câu a ta có đồ thị hàm số y = -x + 3 cắt trục Ox tại B (3; 0)

    C là giao điểm của hai hàm số nên ta có phương trình hoành độ giao điểm

    x + 1 = - x + 3

    ⇔x + x = 3 – 1

    ⇔2x = 2

    ⇔x = 1

    ⇔y = 2.

    Vậy C (1; 2)

    c) Vì A, B đều năm trên trục hoành, nên nhìn vào đồ thị ta thấy AB = 4cm.

    Gọi H là hình chiếu của C lên trục hoành, do đó CH vuông góc với AB, CH là đường cao của tam giác ABC.

    Qua đồ thị ta thấy H(1; 2) ⇒ CH = 2cm

    Diện tích tam giác ABC là: 

    SABC=12AB.CH=12.2.4=4cm2

    Vì A, và H đều nằm trên trục hoành nên qua đồ thị ta thấy AH = 2cm

    Vì CHA là tam giác vuông tại H nên ta có:

    AC2=AH2+CH2 (định lý Py – ta – go)

    ⇔AC2=22+22=8⇒AC=8 cm

    Tương tự ta tính được CB = 8cm

    Chu vi tam giác ABC là

    C = AB + BC + CA = 4 +8 +8 = 4 + 28 (cm).

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Bài 18 trang 52 Toán 9 Tập 1: a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 1...

    Bài 19 trang 52 Toán 9 Tập 1: Đồ thị của hàm số...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,148 03/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: