Nội dung bài viết

    Xem thêm

    TOP 10 đề thi Học kì 1 Toán 9 (Kết nối tri thức) 2024 có đáp án

    Bộ đề thi Học kì 1 Toán lớp 9 Kết nối tri thức năm 2024 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 9 Học kì 1. Mời các bạn cùng đón xem:

    1 367 09/12/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Chỉ từ 180k mua trọn bộ Đề thi Toán 9 Học kì 1 Kết nối tri thức bản word có lời giải chi tiết:

    B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

    B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

    Xem thử tài liệu tại đây: Link tài liệu

    Đề thi Học kì 1 Toán 9 (Kết nối tri thức) 2024 có đáp án

    Phòng Giáo dục và Đào tạo ...

    Đề thi Học kì 1 - Kết nối tri thức

    Năm học ...

    Môn: Toán lớp 9

    Thời gian làm bài: phút

    (Đề 1)

    A. TRẮC NGHIỆM (3,0 điểm)

    Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn

    Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

    Câu 1. Trong các cặp số sau, cặp số nào là nghiệm của phương trình $3x + 2y = 7$?

    A. $\left( {1\,;\,\, - 2} \right).$

    B. $\left( {1\,;\,\,2} \right).$

    C. $\left( { - 1\,;\,\,2} \right).$

    D. $\left( {2\,;\,\,1} \right).$

    Câu 2. Cho $m > n$, khẳng định nào sau đây là đúng?

    A. $m - 3 > n - 3.$

    B. $m + 3 < n + 3.$

    C. $m - 2 < n - 2.$

    D. $n + 2 > m + 2.$

    Câu 3. Cho tam giác $MNP$ vuông tại $M$. Khi đó, $\cot \widehat {MNP}$ bằng

    A. $\frac{{MP}}{{MN}}.$

    B. $\frac{{MN}}{{MP}}.$

    C. $\frac{{MN}}{{NP}}.$

    D. $\frac{{MP}}{{NP}}.$

    Câu 4. Góc ở tâm là góc

    A. có đỉnh nằm trên đường tròn.

    B. có đỉnh nằm trên bán kính của đường tròn.

    C. có hai cạnh là hai đường kính của đường tròn.

    D. có đỉnh trùng với tâm đường tròn.

    Phần 2. Câu trắc nghiệm đúng sai

    Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

    Câu 5. Cho biểu thức $P = \sqrt {{a^2}{b^4}} .$

    a) Khi $P = 0$ thì $a = 0$ và $b = 0.$

    b) Điều kiện của $a$ và $b$ để biểu thức $P$ có nghĩa là $a \ge 0$ và

    c) Với a = - 2, b = - 1 thì giá trị của biểu thức P là 2.

    d) Biểu thức \[P = \left| a \right| \cdot {b^2}.\]

    Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

    Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

    Câu 6. Cho hệ phương trình x−5y=21−6x+3y=−45. Biết cặp số (xo; yo) là nghiệm của hệ phương trình. Tính giá trị của T = xo + yo

    Câu 7. Cho phương trình $\left( {\frac{2}{5}x + 1} \right)\left( {2 - 5x} \right) = 0$. Tính hiệu giữa nghiệm lớn và nghiệm bé của phương trình đó (kết quả đưa về dạng số thập phân).

    B. TỰ LUẬN (7,0 điểm)

    Bài 1. (2,0 điểm)

    1. Giải các phương trình, bất phương trình sau.

    a) $\frac{{x + 2}}{{x - 2}} + \frac{{x - 2}}{{x + 2}} = \frac{{{x^2} + 16}}{{{x^2} - 4}}.$

    b) $\frac{{2x - 1}}{3} - \frac{{x + 2}}{2} \ge \frac{{5x + 4}}{6}.$

    2. Giải bài toán sau bằng cách lập hệ phương trình.

    Bác Nam mua một thùng trái cây nặng \[\;18\,\,{\rm{kg}}\] gồm hai loại là táo và xoài. Biết táo có giá $65\,\,000$ đồng/kg, xoài có giá $70\,\,000$ đồng/kg và giá tiền của thùng trái cây là $1\,\,205\,\,000$ đồng. Hỏi bác mua bao nhiêu kg táo và xoài mỗi loại?

    Bài 2. (2,0 điểm) Cho biểu thức A=x−2x+3 và B=3x+6x−4+xx−2:x−9x−3 với x≥0 ;  x≠4 ;  x≠9.

    a) Tính giá trị của biểu thức $A$ khi $x = \frac{{81}}{{16}}.$

    b) Rút gọn biểu thức $B.$

    c) Tìm giá trị lớn nhất của biểu thức $M = A \cdot B.$

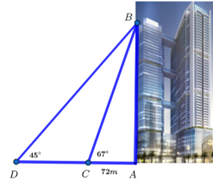
    Bài 3. (1,0 điểm) Tháp chung cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ $67^\circ $ và bóng của tòa nhà trên mặt đất dài khoảng $72{\rm{ m}}$.

    a) Tính chiều cao của tòa tháp chung cư (làm tròn đến kết quả hàng đơn vị).

    TOP 10 đề thi Học kì 1 Toán 9 (Kết nối tri thức) 2024 có đáp án (ảnh 1)

    b) Một flycam từ vị trí $D$ bay lên đỉnh $B$ theo quãng đường $DB$, tạo với phương nằm ngang một góc bằng $45^\circ $. Biết flycam mất $140$ giây để lên đến đỉnh tòa tháp. Tính vận tốc trung bình của chiếc flycam đó (làm tròn kết quả đến hàng phần trăm).

    Bài 4. (2,0 điểm) Cho đường tròn $\left( {O;R} \right)$, đường kính $AB$. Qua $A$ và $B$ vẽ lần lượt hai tiếp tuyến $\left( d \right)$ và $\left( {d'} \right)$ với đường tròn $\left( O \right)$. Một đường thẳng $\alpha $ qua $O$ cắt đường thẳng $\left( d \right)$ ở $M$ và cắt đường thẳng $\left( {d'} \right)$ ở $P$. Từ $O$ vẽ một tia vuông góc với $MP$ và cắt đường thẳng $\left( {d'} \right)$ ở $N.$ Đường thẳng $\alpha $ cắt đường tròn $\left( O \right)$ tại hai điểm $E,F$ ($E$ nằm giữa $O$ và $M).$

    a) Chứng minh $OM = OP$.

    b) Hạ $OI \bot MN$. Chứng minh $MN$ là tiếp tuyến của $\left( O \right)$ và $MA.BN = {R^2}.$

    c) Cho $OM = 2R$. Tính diện tích hình quạt giới hạn bởi $OI,OF$ và cung nhỏ \[IF\].

    d) Gọi $K = AN \cap BM$. Cho $IB = \sqrt 3 IA$, tính diện tích tam giác $KAB$ theo $R$.

    ĐÁP ÁN

    Phần I. TRẮC NGHIỆM (3,0 điểm)

    Bảng đáp án trắc nghiệm:

    Câu

    1

    2

    3

    4

    5a

    5b

    5c

    5d

    6

    7

    Đáp án

    B

    A

    B

    D

    S

    S

    Đ

    S

    3

    2,9

    ...........................................

    ...........................................

    ...........................................

    Tham khảo các loạt bài Đề thi các môn lớp 9 - Kết nối tri thức khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 367 09/12/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: