Nội dung bài viết

    Xem thêm

    TOP 10 đề thi Học kì 1 Toán 9 (Chân trời sáng tạo) năm 2024 có đáp án

    Bộ đề thi Học kì 1 Toán 9 (Chân trời sáng tạo) năm 2024 có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 9 Học kì 1. Mời các bạn cùng đón xem:

    1 35 09/12/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Chỉ từ 180k mua trọn bộ Đề thi Toán 9 học kì 1 Chân trời sáng tạo bản word có lời giải chi tiết:

    B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

    B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

    Xem thử tài liệu tại đây: Link tài liệu

    Bộ đề thi Học kì 1 Toán 9 (Chân trời sáng tạo) năm 2024 có đáp án

    Phòng Giáo dục và Đào tạo ...

    Đề thi Học kì 1 - Chân trời sáng tạo

    Năm học ...

    Môn: Toán lớp 9

    Thời gian làm bài: phút

    (Đề 1)

    A. TRẮC NGHIỆM (2,0 điểm)

    Câu 1. Điều kiện xác định của phương trình $\frac{{x + 2}}{{x + 4}} - 1 = \frac{{30}}{{\left( {x - 3} \right)\left( {x + 4} \right)}}$ là

    A. x≠−3,x≠4.

    B. x<−3,x>4.

    C. x≠3,x≠−4.

    D. x≠−3,x≠2,x≠4.

    Câu 2. Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?

    A. $\frac{x}{2} + \frac{y}{3} = 4.$

    B. $3x - 0y - 2 = 0.$

    C. $3y - 2z = \frac{1}{2}.$

    D. $\frac{2}{x} + \frac{y}{3} - 2 = 0.$

    Câu 3. Bất đẳng thức $n \le 3$ có thể được phát biểu là

    A. $n$ lớn hơn $3.$

    B. $n$ nhỏ hơn $3.$

    C. $n$ không lớn hơn $3.$

    D. $n$ không nhỏ hơn $3.$

    Câu 4. Điều kiện xác định của biểu thức $A = \sqrt {{x^2} + 6} $ là

    A. x > - 6

    B. x≥−6

    C. $x \in \emptyset $.

    D. x∈ℝ.

    Câu 5. Cho $A = 2\sqrt[3]{3}$ và $B = \sqrt[3]{{25}}$. Chọn khẳng định đúng trong các khẳng định sau:

    A. $A > B.$

    B. $A = B.$

    C. $A < B.$

    D. Không so sánh được.

    Câu 6. Nếu $\alpha $ là góc nhọn thì sin90°−α bằng

    A. $\sin \alpha .$

    B. $\tan \alpha .$

    C. $\cos \alpha .$

    D. $\cot \alpha .$

    Câu 7. Số đo góc nội tiếp bằng

    A. số đo cung bị chắn.

    B. một nửa số đo cung bị chắn.

    C. hai lần số đo cung bị chắn.

    D. góc ở tâm cùng chắn cùng một cung.

    Câu 8. Cho đường tròn $\left( O \right)$ có bán kính bằng $5{\rm{ cm}}$ khoảng cách từ tâm $O$ đến dây cung $CD$ là ${\rm{4 cm}}{\rm{.}}$ Độ dài dây cung $CD$ là

    A. \[{\rm{6\;cm}}.\]

    B. \[\frac{{\sqrt 5 {\rm{\;}}}}{2}{\rm{cm}}.\]

    C. \[\sqrt 5 {\rm{\;cm}}.\]

    D. \[{\rm{3\;cm}}.\]

    B. TỰ LUẬN (8,0 điểm)

    Bài 1. (2,0 điểm) Cho hai biểu thức A=x+52x−1 và B=x+1x−1+x−1x+1−3x+1x−1 với x≥0;x≠1;x≠14.

    a) Tính giá trị của biểu thức $A$ khi $x = \frac{1}{{16}}.$

    b) Chứng minh rằng B=2x−1x+1.

    c) Tìm $x$ để biểu thức $M = A.B$ đạt giá trị lớn nhất.

    Bài 2. (2,0 điểm)

    1. Giải các phương trình và bất phương trình sau:

    a) \[\frac{1}{{x + 1}} - \frac{5}{{x - 2}} = \frac{{15}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}.\]

    b) $\frac{{5x - 3}}{5} + \frac{{2x + 1}}{4} \le \frac{{2 - 3x}}{2} - 5$.

    2. Giải bài toán sau bằng cách lập hệ phương trình:

    Người ta trộn $4{\rm{ kg}}$ chất lỏng loại I với ${\rm{3 kg}}$ chất lỏng loại II thì được một hỗn hợp có khối lượng riêng là ${\rm{700 kg/}}{{\rm{m}}^3}$. Biết khối lượng riêng của chất lỏng loại I lớn hơn khối lượng riêng của chất lỏng loại II là ${\rm{200 kg/}}{{\rm{m}}^3}$. Tính khối lượng riêng của mỗi chất.

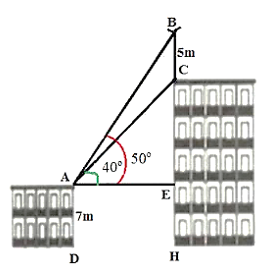
    Bài 3. (1,0 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao $5{\rm{ m}}$. Từ vị trí quan sát $A$ cao $7{\rm{ m}}$ so với mặt đất, có thể nhìn thấy đỉnh $B$ và đỉnh $C$ của một cột ăng – ten dưới góc $50^\circ $ và $40^\circ $ so với phương nằm ngang. Tính chiều cao của tòa nhà.

    TOP 10 đề thi Học kì 1 Toán 9 (Chân trời sáng tạo) năm 2024 có đáp án (ảnh 1)

    Bài 4. (2,5 điểm) Cho đường tròn \[\left( O \right)\] và điểm \[A\] nằm bên ngoài đường tròn. Từ \[A\] kẻ hai tiếp tuyến \[AM,AN\] với đường tròn \[\left( O \right)\]. Một đường thẳng \[d\] đi qua \[A\] cắt đường tròn \[\left( O \right)\] tại hai điểm \[B\] và \[C\] (\[AB < AC\], \[d\] không đi qua tâm \[O\]). Gọi \[I\] là trung điểm của \[BC\]. Đường thẳng \[NI\] cắt đường tròn \[\left( O \right)\] tại điểm thứ hai là \[F\].

    a) Chứng minh bốn điểm \[A,M,O,N\] cùng thuộc một đường tròn.

    b) Chứng minh \[A{N^2} = AB.AC\] và \[MF\parallel AC\].

    c) Hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[B\] và \[C\] cắt nhau tại \[K\]. Chứng minh \[K\] thuộc một đường tròn cố định khi \[d\] thay đổi và thỏa mãn điều kiện đầu bài.

    Bài 5. (0,5 điểm) Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng $72{\rm{ }}{{\rm{m}}^3}$. Đáy bể có dạng hình chữ nhật với chiều rộng là $x{\rm{ }}\left( {\rm{m}} \right)$, chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì $x$ phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

    TOP 10 đề thi Học kì 1 Toán 9 (Chân trời sáng tạo) năm 2024 có đáp án (ảnh 1)

    ĐÁP ÁN

    PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

    Bảng đáp án trắc nghiệm:

    Câu

    1

    2

    3

    4

    5

    6

    7

    8

    Đáp án

    C

    D

    C

    D

    C

    C

    B

    A

    ................................

    ................................

    ................................

    Tham khảo các loạt bài Đề thi các môn lớp 9 - Chân trời sáng tạo khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 35 09/12/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: