TOP 10 đề thi Học kì 1 Toán 12 (Cánh diều) 2024 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Toán 12 Học kì 1 Cánh diều bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Học kì 1 Toán 12 (Cánh diều) có đáp án

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Cánh diều

Năm học ...

Môn: Toán 12

Thời gian làm bài: phút

(Đề 1)

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Cho hàm số \(y = f(x)\) có đồ thị là đường cong hình bên

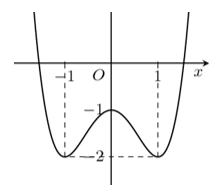
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. \((1; + \infty )\).

B. \((0;1)\).

C. \(( - 1;0)\).

D. \(( - \infty ;0)\).

Câu 2. Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ sau

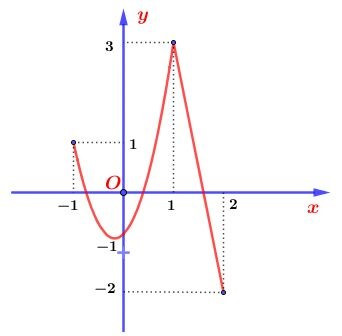
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \[\left[ { - 1;2} \right]\] là

A. \[3\].

B. \[ - 1\].

C. \[1\].

D. \[2\]

Câu 3. Hàm số \[y = {\log _5}\left( {10x - {x^2}} \right)\] đồng biến trên khoảng nào trong các khoảng dưới đây?

A. \(\left( {5;10} \right)\).

B. \(\left( {0;10} \right)\).

C. \(\left( {0;5} \right)\).

D. \(\left( {10;\, + \infty } \right)\).

Câu 4. Gọi \(m\) và \(M\) lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = {e^{2 - 3x}}\) trên đoạn \(\left[ {0\,;\,2} \right].\) Mối liên hệ giữa \(M\) và \(m\) là

A. \(M - m = e\).

B. \(m + M = 1\).

C. \(m.M = \frac{1}{{{e^2}}}\).

D. \(\frac{M}{m} = {e^2}\).

Câu 5. Cho hình hộp \[ABCD.A'B'C'D'\]. Vectơ $\overrightarrow{u}=\overrightarrow{B{B}^{\text{'}}}+\overrightarrow{BA}+\overrightarrow{BC}$ bằng vectơ nào dưới đây?

A. \(\overrightarrow {BD} \).

B. \(\overrightarrow {BD'} \).

C. \(\overrightarrow {BC} \).

D. \(\overrightarrow {BA'} \).

Câu 6. Trong không gian \(Oxyz\), biết $\overrightarrow{OM}=2\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}$. Toạ độ của điểm \(M\) là

A. \(\left( { - 2;3; - 1} \right)\).

B. \(\left( {2; - 3;1} \right)\).

C. \(\left( { - 3;2;1} \right)\).

D. \(\left( {2;1; - 3} \right)\).

Câu 7. Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( { - 2;\,1;\,0} \right)\), \(B\left( {0;\, - 2;\,5} \right)\), \(C\left( {6; - 2;1} \right)\). Tích vô hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là

A. \(\sqrt {38} .\sqrt {52} \).

B. \( - \sqrt {38} .\sqrt {52} \).

C. \(8\).

D. \( - 8\).

Câu 8. Cho hình lập phương \[ABCD.EFGH\]. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và\(\overrightarrow {EG} \)?

A. \(60^\circ \).

B. \[45^\circ \].

C. \[90^\circ \].

D. \[120^\circ \].

Câu 9. Cho hai điểm \(M\left( {0\,;\,0\,;\,2} \right)\) và \(N\left( {4\,;\, - 2;\,6} \right)\). Tìm tọa độ điểm \(P\) sao cho \(N\) là trung điểm của \(MP\)?

A. \(P\left( {2\,;\, - 1\,;\,4} \right)\).

B. \(\left( {4\,;\, - 2\,;\,4} \right)\).

C. \(\left( {2\,;\, - 1\,;\,2} \right)\).

D. \(P\left( {8\,;\, - 4\,;\,10} \right)\).

Câu 10. Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ $\overrightarrow{u}=\left(3;-1;1\right)$ và \$\overrightarrow{v}=\left(1;2;-2\right)$. Độ dài của vectơ $\overrightarrow{u}+\overrightarrow{v}$ là

A. \(\sqrt {10} \).

B. $\sqrt{11}+3$.

C. \(3\sqrt 2 \).

D. \(5\).

Câu 11. Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được thống kê ở bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A.\(0,192\).

B. \(0,197\).

C. \(0,037\).

D. \(0,2\).

Câu 12. Bốn bạn Ánh, Ba, Châu, Dũng cùng là thành viên của một câu lạc bộ rubik. Trong một lần luyện tập rubik với nhau, mỗi bạn đã cùng giải rubik 30 lần liên tiếp và thống kê kết quả lại ở bảng sau:

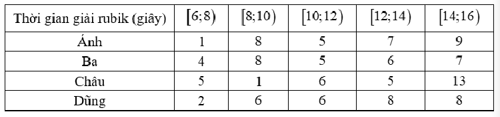
Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì bạn nào có tốc độ giải rubik đồng đều nhất?

A. Ánh.

B. Ba.

C. Châu.

D. Dũng.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây :

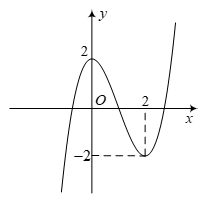
a) Hàm số đạt cực đại tại\(x = 2\).

b) Có 3 giá trị nguyên của \(m\)để phương trình \(f\left( x \right) = m\)có 3 nghiệm phân biệt .

c) Đường cong trên là đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\).

d) Gọi \(M\)và \(m\)lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {2\sin x + 1} \right)\)thì \(M + m = 5\).

Câu 2. Cho hàm số \(y = \frac{{x - 1}}{{2x - 3}}\) \[\left( C \right)\].

a) Tiệm cận đứng của hàm số là \(x = \frac{3}{2}\).

b) Tọa độ giao điểm hai đường tiệm cận thuộc đường thẳng \(x - y - 1 = 0\)

c) Đường thẳng \(2x + y - 1 = 0\) cắt tiệm cận đứng, tiệm cận ngang của hàm số tại các điểm A và B. Diện tích của tam giác \(IAB\) bằng \(\frac{{25}}{4}\), với \(I\)là giao điểm hai đường tiệm cận.

d) Gọi \(I\) là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ \(I\) đến một tiếp tuyến bất kỳ của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng \(\frac{1}{{\sqrt 2 }}\).

Câu 3. Trong không gian \(Oxyz\), cho vectơ $\overrightarrow{OA}=\left(2;-1;5\right)$ và điểm \(B\left( {5; - 5;7} \right)\).

a) Tọa độ của điểm \(A\) là \(\left( {2; - 1;5} \right)\).

b) Gọi \(C\left( {a;b;c} \right)\) thỏa mãn \(\Delta ABC\) nhận \(G\left( {1;1;1} \right)\) làm trọng tâm. Khi đó \(a + b + c = - 4\).

c) Nếu \(A,B,M\left( {x;y;1} \right)\) thẳng hàng thì tổng \(x + y = 3\).

d) Cho \(N \in \left( {Oxy} \right)\) để \(\Delta ABN\) vuông tại \(A\). Tổng hoành độ và tung độ của điểm \(N\) bằng 3.

Câu 4. Giả sử kết quả khảo sát hai khu vực \(A\) và \(B\) về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: \(15\) (tuổi).

b) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: \(12\)(tuổi).

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm ứng với khu vực A là: \(\frac{{61}}{3}\) (tuổi).

d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.

Câu 1. Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \(h\,\,\left( {\rm{m}} \right)\) của mực nước trong kênh tại thời điểm \(t\,\,\left( {\rm{h}} \right)\,\,\left( {0 \le t \le 24} \right)\) trong ngày được xác định bởi công thức \(h = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\). Gọi \(\left( {a\,;\,b} \right)\) là khoảng thời gian trong ngày mà độ sâu của mực nước trong kênh tăng dần. Tính giá trị của \(a + b\).

Câu 2. Một ông nông dân có \(240\)m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu m²?

Câu 3. Một doanh nghiệp cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy \(A\) và \(B\). Máy \(A\) làm việc trong \(x\) ngày cho số tiền lãi là \({x^2} + 2x\) (triệu đồng), máy \(B\) làm việc trong \(y\) ngày cho số tiền lãi là \( - 27{y^2} + 326y\) (triệu đồng). Hỏi doanh nghiệp đó cần sử dụng máy \(A\) làm việc trong bao nhiêu ngày để số tiền lãi thu được nhiều nhất? Biết rằng hai máy \(A\) và \(B\) không đồng thời làm việc và máy \(B\) làm việc không quá 6 ngày.

Câu 4. Trong không gian tọa độ \(Oxyz\), gọi \(A,B,C\) lần lượt là hình chiếu của \[M\left( {3;3;3} \right)\] lên

các trục tọa độ \(Ox,Oy,Oz\). Giả sử \[H\left( {a;b;c} \right)\] là trực tâm tam giác \(ABC\). Tính \[{a^2} + {b^2} + {c^2}\].

Câu 5. Cho tứ diện ABCD có \(AB = AC = AD = 1.\) và \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên cạnh \(AB\) sao cho \(AI = 3IB\) và \(J\) là trung điểm của \(CD\). Tính độ dài đoạn thẳng \[IJ\]và làm tròn kết quả đến hàng phần trăm.

Câu 6. Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông

Tính phương sai của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm).

.............................................

.............................................

.............................................

==========================

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Cánh diều

Năm học ...

Môn: Toán 12

Thời gian làm bài: phút

(Đề 2)

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

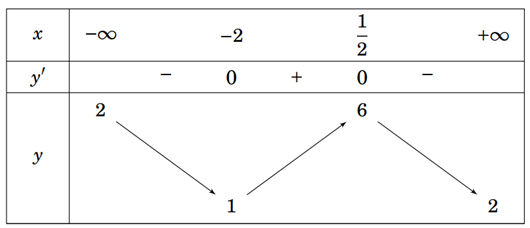
Câu 1. Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình vẽ.

Chọn khẳng định đúng trong các khẳng định sau:

A. Giá trị nhỏ nhất của hàm số y = f(x) trong khoảng (-∞;-2) là 1.

B. Giá trị lớn nhất của hàm số y = f(x) trong khoảng $\left(-\infty ;\frac{1}{2}\right)$ là 6.

C. Giá trị nhỏ nhất của hàm số y = f(x) trong khoảng $\left(-2;\frac{1}{2}\right)$ là 1.

D. Hàm số y = f(x) không có giá trị nhỏ nhất trên khoảng (-2;+∞).

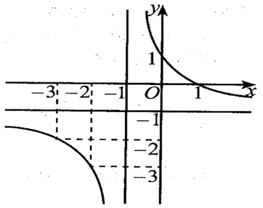
Câu 2. Cho hàm số y = f(x) có đồ thị như hình bên dưới. Đường thẳng nào sau đây là đường tiệm cận ngang của đồ thị hàm số đã cho?

A. x = 1.

B. x = -1.

C. y = 1.

D. y = -1.

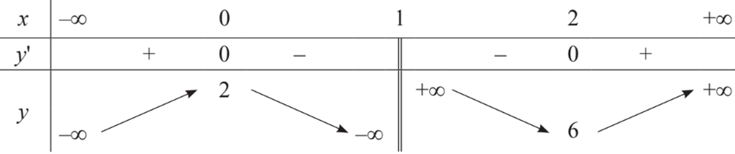
Câu 3. Bảng biến thiên sau là của hàm số nào dưới đây?

A. $y=\frac{x^2+2x-2}{x-1}$.

B. $y=\frac{x^2+2x-2}{x+1}$.

C. $y=\frac{x^2+2x+2}{x-1}$.

D. $y=\frac{x^2+2x+2}{x+1}$.

Câu 4. Có bao nhiêu giá trị nguyên của tham số m sao cho ứng với mỗi m, hàm số $y=\frac{1}{3}{x}^3+x^2-mx-1$ có đúng một điểm cực trị thuộc khoảng (0;4) ?

A. 23.

B. 8.

C. 9.

D. Vô số.

Câu 5. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(3;-4-0). Toạ độ $\overrightarrow{OA}$ là

A. (3;0;0).

B. (3;-4;0).

C. (0;-4;0).

D. (0;0;0).

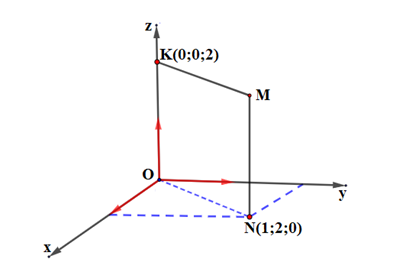
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho hình chữ nhật OKMN (hình vẽ bên).

Tọa độ đỉnh M của hình chữ nhật là:

A. M(1;2;2).

B. M(-1;-2;-2).

C. M(0;2;2).

D. M(1;2;0).

Câu 7. Trong không gian với hệ tọa độ Oxyz, với $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz. Tính tọa độ của vecto $\overrightarrow{i}+\overrightarrow{j}-\overrightarrow{k}$.

A. (-1;-1;1).

B. (-1;1;1).

C. (1;1;-1).

D. (1;-1;1).

Câu 8. Cho điểm M(3;-2;0); N(2;4;1). Tọa độ của $\overrightarrow{MN}$ là:

A. (1;-6;-1).

B. (-1;6;1).

C. (1;0;6).

D. (-1;6;-1).

Câu 9. Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{OM}=\left(1;5;2\right)$, $\overrightarrow{ON}=\left(3;7;-4\right)$, K(-1;3;1). Gọi P là điểm đối xứng với M qua N. Tìm tọa độ vectơ $\overrightarrow{KP}$.

A. $\overrightarrow{KP}=\left(6;6;-11\right)$.

B. $\overrightarrow{KP}=\left(8;6;-11\right)$.

C. $\overrightarrow{KP}=\left(6;6;-4\right)$.

D. $\overrightarrow{KP}=\left(3;3;-2\right)$.

Câu 10. Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có điểm A trùng với gốc tọa độ O, điểm B nằm trên tia Ox, điểm D nằm trên tia Oy, điểm A' nằm trên tia Oz. Biết AB = 2, AD = 4, AA' = 3. Gọi tọa độ của C' là (a;b;c) khi đó biểu thức A + b - c có giá trị là.

A. -4.

B. 9.

C. 3.

D. 6.

Câu 11. Đại lượng nào đo độ phân tán của nửa giữa của mẫu số liệu, không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu?

A. Khoảng biến thiên.

B. Khoảng tứ phân vị.

C. Phương sai.

D. Độ lệch chuẩn.

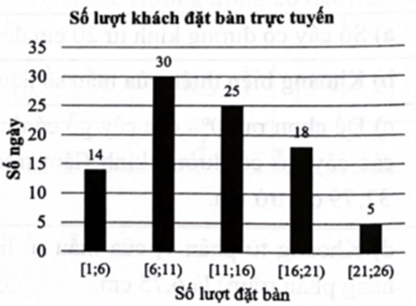
Câu 12. Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn;... Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.

A. 8.

B. 8,5.

C. 7,5.

D. 16.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số y = f(x) = $-x+1-\frac{1}{x-1}$.

a) Đường thẳng y = x - 1 là tiệm cận xiên của đồ thị hàm số y = f(x).

b) Đạo hàm của hàm số y = f(x) là $f^{\text{'}}\left(x\right)=\frac{2x-x^2}{{\left(x-1\right)}^2},x\ne 1$.

c) Giá trị cực tiểu của hàm số y = f(x) là -2.

d) Bất phương trình x² + (m - 2)x - m + 2 ≥ 0 nghiệm đúng với mọi x > 1 nếu m ≥ -2.

Câu 2. Nồng độ thuốc C(t) tính theo mg/cm³ trong máu của bệnh nhân được tính bởi $C\left(t\right)=\frac{\mathrm{0,05}t}{t^2+t+1}$, trong đó t là thời gian tính theo giờ kể từ khi tiêm cho bệnh nhân.

a) Hàm số C(t) có đạo hàm $C^{\text{'}}\left(t\right)=\frac{1-t^2}{20{\left(t^2+t+1\right)}^2},t\ge 0$.

b) Sau khi tiêm, nồng độ thuốc trong máu của bệnh nhân giảm dần theo thời gian.

c) Nồng độ thuốc trong máu lớn nhất ở thời điểm 1 giờ sau khi tiêm.

d) Có thời điểm nồng độ trong máu của bệnh nhân đạt 0,02 mg/cm³.

Câu 3. Cho tứ diện đều ABCD cạnh a. E là điểm trên đoạn CD sao cho ED = 2CE.

a) Có 6 vectơ (khác vectơ $\overrightarrow{0}$) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.

b) Góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{BC}$ bằng 60°.

c) Nếu $\overrightarrow{BE}=m\overrightarrow{BA}+n\overrightarrow{BC}+p\overrightarrow{BD}$ thì $m+n+p=\frac{2}{3}$.

d) Tích vô hướng $\overrightarrow{AD}.\overrightarrow{BE}=\frac{a^2}{6}$.

Câu 4. Cho bảng số liệu dưới đây về thời gian (phút) tập thể dục buổi sáng của hai bạn Bình và Chi trong 30 ngày.

a) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục của Chi là 25 (phút).

b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là: $Q_1=\frac{354}{16}$.

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Chi là 8,75.

d) Phương sai của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là $\frac{314}{9}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.

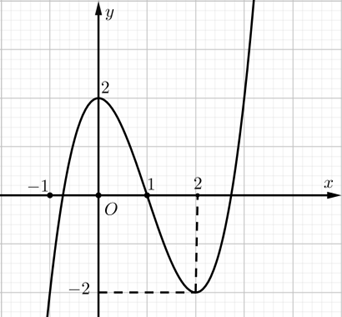
Câu 1. Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình sau. Phương trình f(f(x)) = 0 có bao nhiêu nghiệm thực phân biệt?

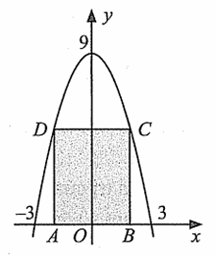
Câu 2. Cho hình chữ nhật ABCD có hai đỉnh di động trên đồ thị hàm số y = 9 - x² trên khoảng (-3;3), hai đỉnh còn lại nằm trên trục hoành (tham khảo hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật ABCD (kết quả làm tròn đến hàng phần mười).

Câu 3. Bác Tôm có một cái ao có diện tích 50 m² để nuôi cá. Vụ vừa qua bác nuôi với mật độ 20 con/m² và thu được tất cả 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá thu được, bác thấy cứ thả giảm đi 8 con/m² thì tương ứng sẽ có mỗi con cá thành phẩm thu được tăng thêm 0,5 kg. Hỏi vụ tới bác phải mua bao nhiêu con cá giống để đạt được tổng khối lượng cá thành phẩm cao nhất? (giả sử không có hao hụt trong quá trình nuôi).

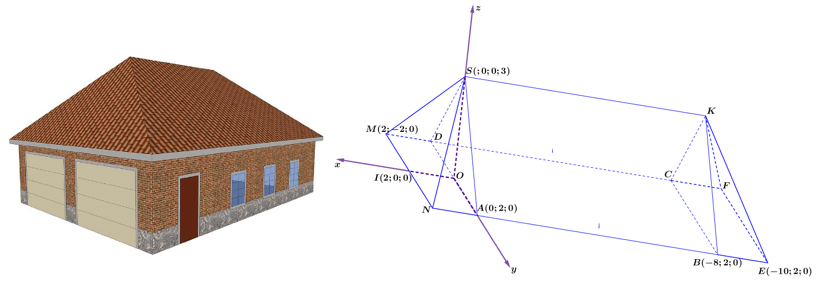
Câu 4. Phần mái của một căn nhà có dạng là khối đa diện được mô tả và gắn trên hệ trục tọa độ Oxyz như hình vẽ. Tính thể tích khối đa diện của mái nhà.

Câu 5. Một công ty viễn thông đang lên kế hoạch xây dựng một tháp viễn thông tại một thành phố để cung cấp dịch dụ tốt hơn. Công ty cần xác định vị trí của tháp sao cho có thể phủ sóng hiệu quả đến ba toà nhà quan trọng trong thành phố. Giả sử các toà nhà này được đặt tại các vị trí có toạ độ như sau:

Toà nhà A(0;0;0)

Toà nhà B(6;0;0)

Toà nhà $C\left(3;\sqrt{3};2\sqrt{6}\right)$

Tháp viễn thông phải đặt ở vị trí sao cho tổng khoảng cách từ tháp đến 3 toà nhà là nhỏ nhất. Khi đó tổng khoảng cách từ vị trí của tháp đến ba toà nhà bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm)

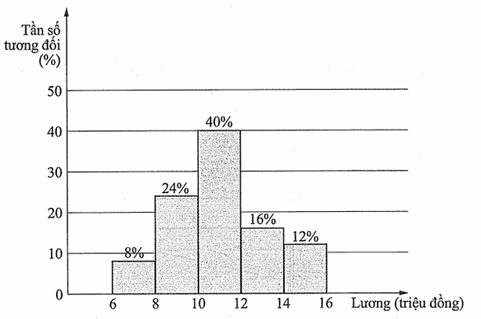
Câu 6. Lương tháng của 50 nhân viên một công ty được biểu diễn ở biểu đồ sau:

Tính khoảng tứ phân vị của mẫu số liệu ghép nhón trên (đơn vị: triệu đồng). Làm tròn kết quả đến hàng phần trăm.

BẢNG ĐÁP ÁN

PHẦN I.

PHẦN II.

PHẦN III.

................................

................................

................................