30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập cuối năm Hình học 10 có đáp án

Cho tam giác ABC, M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Khẳng định nào sau đây là sai?

A. $\vec{A M} = \frac{1}{2} (\vec{A B} + \vec{A C})$

B. $\vec{A M} + \vec{B N} + \vec{C P} = \vec{0}$

C. $\vec{A N} + \vec{B P} + \vec{C M} = \vec{0}$

D. $\vec{A M} + \vec{B N} = \vec{C P}$

Xem đáp án

* Phương án A đúng theo tinh chất trung điểm của đoạn thẳng

* Phương án B: Gọi G là trọng tâm tam giác ABC ta có:

Đáp án D

Câu 2:

13/07/2024

Cho tam giác đều ABC cạnh a, G là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?

A. $|\vec{A G}| = \frac{a \sqrt{3}}{2}$

B. $|\vec{A G} + \vec{B G}| = a$

C. $|\vec{A G} + \vec{B G} + \vec{C G}| = 0$

D. $|\vec{A G} + \vec{B G} + \vec{C G}| = \vec{0}$

Xem đáp án

Nếu G là trong tâm tam giác ABC thì

$\begin{array}{l} \vec{G A} + \vec{G B} + \vec{G C} = \vec{0} \Leftrightarrow \vec{A G} + \vec{B G} + \vec{C G} = \vec{0} \\ \Leftrightarrow |\vec{A G} + \vec{B G} + \vec{C G}| = |\vec{0}| = 0 \end{array}$

Đáp án C

Câu 3:

19/07/2024

Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $|\vec{A M} + \vec{B M}| = 2 |\vec{C M}|$

A. Một đường thẳng

B. Một đường tròn

C. Một tia

D. Một điểm

Xem đáp án

Đáp án A

Câu 4:

Cho hình bình hành ABCD và các điểm M, N thỏa mãn $\vec{A M} = 2 \vec{A B} + 3 \vec{A D}; \vec{A N} = x \vec{A B} + 5 \vec{A D}$ . Để ba điểm M, N, C thẳng hàng thì:

A. x = 1

B. x = 3

C. x = 5

D. x = 7

Xem đáp án

Đáp án A

Câu 5:

18/07/2024

Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của CM. Khẳng định nào sau đây là đúng?

A. $\vec{A N} = \frac{1}{2} \vec{A B} + \frac{2}{3} \vec{A C}$

B. $\vec{A N} = \frac{3}{4} \vec{A B} + \frac{1}{4} \vec{A C}$

C. $\vec{A N} = \frac{1}{4} \vec{A B} + \frac{1}{2} \vec{A C}$

D. $\vec{A N} = \frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C}$

Xem đáp án

Ta có, N là trung điểm của MC nên:

$\begin{array}{l} \vec{A N} = \frac{1}{2} (\vec{A M} + \vec{A C }) = \frac{1}{2} \vec{A M} + \frac{1}{2} \vec{A C} \\ = \frac{1}{2} . \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C} = \frac{1}{4} \vec{A B} + \frac{1}{2} \vec{A C} \end{array}$

Đáp án C

Câu 6:

Cho hai vectơ không cùng phương $\vec{a}, \vec{b}$ . Vectơ nào sau đây cùng phương với vectơ $3 \vec{a} - 4 \vec{b}$ ?

A. $4 \vec{a} - 3 \vec{b}$

B. $3 \vec{a} + 4 \vec{b}$

C. $- 4 \vec{a} - 3 \vec{b}$

D. $\frac{3}{4} \vec{a} - \vec{b}$

Xem đáp án

Đáp án D

Câu 7:

Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?

A. $\vec{A C} = \vec{B D} .$

B. $\vec{A B} + \vec{A C} + \vec{A D} = \vec{0} .$

C. $|\vec{A B} - \vec{A D}| = |\vec{A B} + \vec{A D}| .$

D. $|\vec{B C} + \vec{B D}| = |\vec{A C} - \vec{A B}| .$

Xem đáp án

Câu 8:

11/07/2024

Cho các điểm A, B, C, D, E, F. Khi đó $\vec{E B} + \vec{D E} + \vec{A C} + \vec{B F} + \vec{C D}$ bằng vectơ nào trong các vectơ sau đây?

A. $\vec{A E}$

B. $\vec{A F}$

C. $\vec{A D}$

D. $\vec{A C}$

Xem đáp án

Đáp án B

Câu 9:

11/07/2024

Cho hình vuông ABCD có tọa độ đỉnh A(1;2) và tâm hình vuông là I(-1; -4). Khi đó phương trình của đường chéo BD là:

A. x + 3y + 13 = 0

B. 3x – y + 1 = 0

C. x – y – 3 = 0

D. x + y + 5 = 0

Xem đáp án

Đáp án A

Câu 10:

13/07/2024

Cho tam giác ABC vuông cân tại C và $A B = \sqrt{2} .$ Tính độ dài của $\vec{A B} + \vec{A C} .$

A. $|\vec{A B} + \vec{A C}| = \sqrt{5} .$

B. $|\vec{A B} + \vec{A C}| = 2 \sqrt{5} .$

C. $|\vec{A B} + \vec{A C}| = \sqrt{3} .$

D. $|\vec{A B} + \vec{A C}| = 2 \sqrt{3} .$

Xem đáp án

Đáp án A

Câu 11:

Cho tam giác ABC có đỉnh A(1; 1), B(-2; 4) và G(1; 2) là trọng tâm của tam giác. Khi đó tọa độ đỉnh C là:

A. C(0; 7/3)

B. C(4; 1)

C. C(2; -3)

D. C(-2; 2)

Xem đáp án

Đáp án B

Câu 12:

Cho $\vec{a} = (x; 2), \vec{b} = (- 5; 1), \vec{c} = (x; 7) .$ Tìm x biết $\vec{c} = 2 \vec{a} + 3 \vec{b}$

A. x= - 15

B. x= 3

C. x = 15

D. x= 5

Xem đáp án

Đáp án C

Câu 13:

Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0; 3); D(2; 1) và I(-1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC

A. (1 ; 2)

B. (-2; -3)

C. (-3 ; -2)

D. (- 4 ; -1)

Xem đáp án

Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2)

Gọi N ( $x_{N}; y_{N}$ ) là tọa độ trung điểm của cạnh BC

Do I là tâm của hình chữ nhật nên I là trung điểm của MN.

Suy ra

$\{\begin{cases} x_{N} = 2 x_{I} - x_{M} = - 3 \\ y_{N} = 2 y_{I} - y_{M} = - 2 \end{cases} \Rightarrow N (- 3; - 2) .$

Đáp án C

Câu 14:

21/07/2024

Khẳng định nào sau đây là sai?

A. $\vec{a}, \vec{b}$ cùng phương khi và chỉ khi $|\vec{a} . \vec{b}| = |\vec{a}| . |\vec{b}|$

B. $\vec{a}, \vec{b}$ cùng hướng khi và chỉ khi $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

C. $\vec{a}, \vec{b}$ ngược hướng khi và chỉ khi $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

D. $\vec{a}, \vec{b}$ ngược hướng khi và chỉ khi $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$ hoặc $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

Xem đáp án

Đáp án D

Câu 15:

Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\vec{M A} (\vec{M B} + \vec{M C}) = 0$ là

A. Một điểm

B. Một tia

C. Một đường thẳng

D. Một đường tròn

Xem đáp án

Đáp án D

Câu 16:

21/07/2024

Tam giác ABC có . Điểm M thuộc đoạn BC sao cho MC =2MB. Tính độ dài cạnh AM.

A. $A M = 4 \sqrt{2} .$

B. $A M = 3.$

C. $A M = 2 \sqrt{3} .$

D. $A M = 3 \sqrt{2} .$

Xem đáp án

Câu 17:

19/07/2024

Cho tam giác vuông cân ABC cạnh huyền bằng a. khi đó giá trị của biểu thức tích vô hướng $\vec{A B} . \vec{B C} + \vec{B C} . \vec{C A} + \vec{C A} . \vec{A B}$ là

A. 0

B. $- a^{2}$

C. $- 2 a^{2}$

D. $2 a^{2}$

Xem đáp án

$\begin{array}{l} {(\vec{A B} + \vec{B C} + \vec{C A})}^{2} = {\vec{A B}}^{2} + {\vec{B C}}^{2} + {\vec{C A}}^{2} + 2. (\vec{A B} . \vec{B C} + \vec{B C} . \vec{C A} + \vec{C A} . \vec{A B}) \\ \Leftrightarrow 2. (\vec{A B} . \vec{B C} + \vec{B C} . \vec{C A} + \vec{C A} . \vec{A B}) \\ = {(\vec{A B} + \vec{B C} + \vec{C A})}^{2} = - {\vec{A B}}^{2} - {\vec{B C}}^{2} - \vec{C A} \\ = {\vec{0}}^{2} - A B^{2} - B C^{2} - C A^{2} = 0 - a^{2} - a^{2} = - 2 a^{2} \\ \Leftrightarrow \vec{A B} . \vec{B C} + \vec{B C} . \vec{C A} + \vec{C A} . \vec{A B} = - a^{2} \end{array}$

Đáp án B

Câu 18:

Lý thuyết Tính chất ba đường trung tuyến của tam giác – Toán 7 Cánh diều

Cho hình chữ nhật ABCD có AB = 3, AD = 4. Gọi α là góc tạo bởi hai đường chéo của hình chữ nhật $(0 ° < α \leq 90 °)$ . Khi đó khẳng định nào sau đây là đúng?

A. $\sin α = \frac{24}{25}$

B. $\sin α = \frac{7}{25}$

C. $\cos α = \frac{24}{25}$

D. $\cos α = \frac{- 7}{25}$

Xem đáp án

Ta có: AB = CD = 3cm; AD = BC = 4cm.

Áp dụng định lí Pyta go vào tam giác ABC ta có:

AC² = AB² + BC² = 25 nên AC = 5

Suy ra: BD = AC= 5.

Gọi I là giao điểm hai đường chéo.

Theo tính chất hình chữ nhật thì

Đáp án A

Câu 19:

13/11/2024

Tam giác ABC cân tại C, có AB = 9cm và $A C = \frac{15}{2} cm$ . Gọi D là điểm đối xứng của B qua C. Tính độ dài cạnh AD

A. AD = 6 cm.

B. AD = 9 cm.

C. AD = 12 cm.

D. $A D = 12 \sqrt{2}$ cm.

Xem đáp án

Đáp án đúng là C

Lời giải

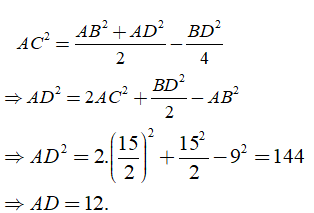
*Phương pháp giải:

Sử dụng công thức trung tuyến đối với tam giác ABD để tính AD

*Lý thuyết

. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

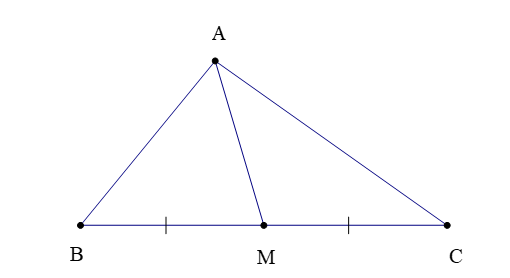
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

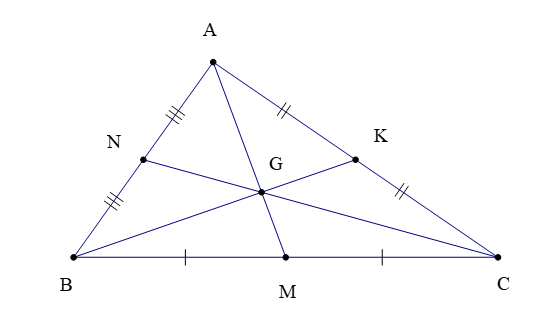
Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Xem thêm

TOP 15 câu Trắc nghiệm Tính chất ba đường trung tuyến của tam giác (Chân trời sáng tạo 2024) có đáp án - Toán 7

Câu 20:

16/07/2024

Cho a $\vec{a} = (x_{1}; y_{1}), \vec{b} (x_{2}; y_{2})$ . Khẳng định nào sau đây là sai?

A. $\vec{a} . \vec{b} = x_{1} y_{1} + x_{2} y_{2}$

B. $|\vec{a}| = \sqrt{{x_{1}}^{2} + {y_{1}}^{2}}$

C. $\vec{a} ⊥ \vec{b} ⟺ x_{1} y_{1} + x_{2} y_{2} = 0$

D. ${|\vec{a} . \vec{b}|}^{2} \leq ({x_{1}}^{2} + {y_{1}}^{2}) ({x_{2}}^{2} + {y_{2}}^{2})$

Xem đáp án

$\vec{a} (x_{1}; y_{1}); \vec{b} (x_{2}; y_{2}) \Rightarrow \vec{a} . \vec{b} = x_{1} x_{2} + y_{1} y {}_{2}$

khẳng định A sai

Đáp án A

Câu 21:

21/07/2024

Cho các điểm A(-2; 1), B(3; 4), C(1; 0). Khi đó $\cos \overset{⏜}{A B C}$ bằng

A. $- \frac{11}{\sqrt{170}}$

B. $\frac{11}{\sqrt{170}}$

C. $- \frac{7}{\sqrt{170}}$

D. $\frac{7}{\sqrt{170}}$

Xem đáp án

Đáp án B

Câu 22:

19/07/2024

Cho các điểm A(-3; 2), B(1; 4). Điểm M trên trục Ox cách đều A và B có tọa độ là

A. $M (\frac{1}{2}; 0)$

B. $M (- \frac{1}{2}; 0)$

C. $M (\frac{3}{2}; 0)$

D. M(4; 0)

Xem đáp án

Đáp án A

Câu 23:

Cho tam giác ABC với A(-2;1),B(3;4), C(1;0). Phương trình đường cao CH của tam giác ABC là

A. 5x – 3y – 5 =0

B. 3x +2y – 3= 0

C. x +2y – 1 = 0

D. 5x +3y – 5 = 0

Xem đáp án

Đáp án D

Câu 24:

Cho α $(0 ° \leq α \leq 90 °)$ là góc tạo bởi hai đường thẳng d1: x + 2y + 4 = 0, d2: 4x - y = 0. Khi đó khẳng định nào sau đây là đúng?

A. $\sin α = \frac{2}{\sqrt{85}}$

B. $\cos α = \frac{- 9}{\sqrt{85}}$

C. $\sin α = \frac{9}{\sqrt{85}}$

D. $\cos α = \frac{- 2}{\sqrt{85}}$

Xem đáp án

Đáp án C

Câu 25:

13/07/2024

Cho hình chữ nhật (H) có đỉnh A(-2;1) và phương trình hai cạnh của hình chữ nhật là x – 2y + 1 = 0 và 2x + y – 4 = 0. Diện tích hình chữ nhật (H) là

A. 19/5

B. 21/5

C. 23/5

D. 5

Xem đáp án

Ta thấy điểm A không thuộc 2 đường thẳng đã cho.

Khoảng cách từ A đến 2 đường thẳng là:

Đáp án B

Câu 26:

Đường tròn (C) đi qua hai điểm A(1; 2); B(3;4) và tiếp xúc với đường thẳng $Δ : 3 x + y - 3 = 0$ . Viết phương trình đường tròn (C), biết tâm của (C) có tọa độ là những số nguyên.

A. $x^{2} + y^{2} - 3 x - 7 y + 12 = 0.$

B. $x^{2} + y^{2} - 6 x - 4 y + 5 = 0.$

C. $x^{2} + y^{2} - 8 x - 2 y - 10 = 0.$

D. $x^{2} + y^{2} - 2 x - 8 y + 20 = 0.$

Xem đáp án

Đáp án D

Câu 27:

Cho đường tròn (C): $x^{2} + y^{2} - 6 x + 8 y - 24 = 0$ và đường thẳng ∆ : x + y – m = 0. Để đường thẳng ∆ cắt (C) theo dây cung AB có độ dài bằng 10 thì giá trị của m là:

A. $m = 1 \pm 4 \sqrt{3}$

B. $m = - 1 \pm 4 \sqrt{3}$

C. $m = - 1 \pm 2 \sqrt{6}$

D. Không tồn tại giá trị của m

Xem đáp án

Đáp án B

Câu 28:

Cho đường tròn (C): $x^{2} + y^{2} - 4 x + 2 y + 1 = 0$ . Để qua điểm A(m+2; 1) kẻ được hai tiếp tuyến với đường tròn (C) và hai tiếp tuyến tạo với nhau một góc 120° thì giá trị m là:

A. $m = \pm 2 \sqrt{2}$

B. $m = \pm 2 \sqrt{3}$

C. $m = \pm \frac{2 \sqrt{3}}{3}$

D. Không tồn tại giá trị của m

Xem đáp án

Đáp án D

Câu 29:

18/07/2024

Cho phương trình $\frac{x^{2}}{4 m + 1} + \frac{y^{2}}{3 m} = 1$ . Để phương trình đã cho là phương trình chính tắc của một elip có tiêu cự bằng 8 thì:

A. m = 7

B. m = 63

C. m = 15

D. m = 1

Xem đáp án

Đáp án C

Câu 30: