Giải SGK Toán lớp 11 – KNTT – Tập 2 Bài 21. Phương trình, bất phương trình mũ và lôgarit
Giải SGK Toán lớp 11 – KNTT – Tập 2 Bài 21. Phương trình, bất phương trình mũ và lôgarit
-
251 lượt thi
-
34 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử dụng được mô hình hóa bằng công thức:
V(t) = 780 ∙ (0,905)t.
Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị).
 Xem đáp án
Xem đáp án
Theo yêu cầu bài ra, ta cần tìm t sao cho V(t) ≤ 300
⇔ 780 ∙ (0,905)t ≤ 300
.
Ta có 9,6 ≈ 10. Vậy sau khoảng 10 năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng.
Câu 2:
22/07/2024Xét phương trình: .
a) Khi viết thành luỹ thừa của 2 thì phương trình trên trở thành phương trình nào?
 Xem đáp án
Xem đáp án
a) Ta có . Khi đó phương trình đã cho trở thành
2x + 1 = 2– 2. (*)
Câu 3:
22/07/2024b) So sánh số mũ của 2 ở hai vế của phương trình nhận được ở câu a để tìm x.
 Xem đáp án
Xem đáp án
b) Vì cơ số ở vế của (*) đều bằng nhau nên số mũ phải bằng nhau, tức là
x + 1 = – 2 ⇔ x = – 3.
Câu 4:
22/07/2024Giải các phương trình sau:
a) ;
 Xem đáp án
Xem đáp án
a)
Đưa vế phải về cơ số 2, ta có .
Khi đó phương trình đã cho trở thành
23x – 1 = 2– x – 1 ⇔ 3x – 1 = – x – 1 ⇔ 4x = 0 ⇔ x = 0.
Vậy phương trình đã cho có nghiệm duy nhất x = 0.
Câu 5:
22/07/2024Giải các phương trình sau:
b) 2e2x = 5.
 Xem đáp án
Xem đáp án
b) 2e2x = 5 ⇔ e2x = .
Lấy lôgarit tự nhiên hai vế của phương trình trên ta được 2x = ln hay x = ln .
Vậy phương trình đã cho có nghiệm duy nhất x = ln .
Câu 6:
22/07/2024Xét phương trình: 2log2x = – 3.
a) Từ phương trình trên, hãy tính log2x.
 Xem đáp án
Xem đáp án
a) Ta có 2log2x = – 3 .
Câu 7:
22/07/2024b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.
 Xem đáp án
Xem đáp án
b) Từ định nghĩa lôgarit ta có:
.
Câu 8:
22/07/2024Giải các phương trình sau:
a) 4 – log(3 – x) = 3;
 Xem đáp án
Xem đáp án
a) 4 – log(3 – x) = 3
Điều kiện: 3 – x > 0 ⇔ x < 3.
Phương trình đã cho trở thành log(3 – x) = 1 ⇔ 3 – x = 101 ⇔ x = – 7 (t/m).
Vậy phương trình đã cho có nghiệm duy nhất x = – 7.
Câu 9:
23/07/2024Giải các phương trình sau:
b) log2(x + 2) + log2(x – 1) = 1.
 Xem đáp án
Xem đáp án
b) log2(x + 2) + log2(x – 1) = 1
Điều kiện: .
Áp dụng tính chất của lôgarit, phương trình đã cho trở thành
log2 [(x + 2)(x – 1)] = 1
⇔ (x + 2)(x – 1) = 21
⇔ x2 + x – 2 = 2
⇔ x2 + x – 4 = 0
.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất .
Câu 10:
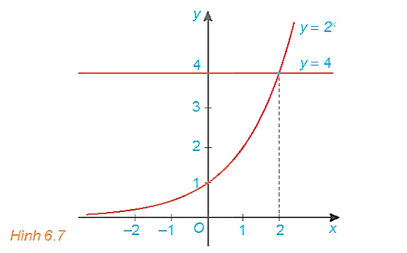
22/07/2024Cho đồ thị của các hàm số y = 2x và y = 4 như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số y = 2x nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình 2x > 4.
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 6.7, ta thấy khoảng giá trị của x mà đồ thị hàm số y = 2x nằm phía trên đường thẳng y = 4 là (2; + ∞).
Vậy tập nghiệm của bất phương trình 2x > 4 là (2; + ∞).
Câu 11:
22/07/2024Giải các bất phương trình sau:
a) 0,12x – 1 ≤ 0,12 – x;
 Xem đáp án
Xem đáp án
a) Ta có:
0,12x – 1 ≤ 0,12 – x
⇔ 2x – 1 ≥ 2 – x (do 0 < 0,1 < 1)
⇔ 3x ≥ 3
⇔ x ≥ 1.
Vậy tập nghiệm của bất phương trình đã cho là [1; + ∞).
Câu 12:
22/07/2024Giải các bất phương trình sau:
b) 3 ∙ 2x + 1 ≤ 1.
 Xem đáp án
Xem đáp án
b) 3 ∙ 2x + 1 ≤ 1
(do 2 > 1)
⇔ x ≤ log23– 1 – 1
⇔ x ≤ – log23 – log22
⇔ x ≤ – log2(3 ∙ 2)
⇔ x ≤ – log26
Vậy tập nghiệm của bất phương trình đã cho là (– ∞; – log26].
Câu 13:
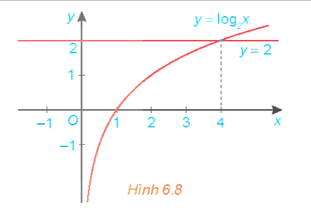
22/07/2024Cho đồ thị của các hàm số y = log2x và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số y = log2x nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình log2 x > 2.
 Xem đáp án
Xem đáp án
Quan sát đồ thị ở Hình 6.8, ta thấy khoảng giá trị của x mà đồ thị hàm số y = log2x nằm phía trên đường thẳng y = 2 là (4; + ∞).
Vậy tập nghiệm của bất phương trình log2 x > 2 là (4; + ∞).
Câu 14:
21/07/2024Giải các bất phương trình sau:
a) ;
 Xem đáp án
Xem đáp án
a)
Điều kiện: .
Bất phương trình đã cho tương đương với
⇔ – log7(x + 1) > log7(2 – x)
⇔ log7(x + 1)– 1 > log7(2 – x)
⇔ (x + 1)– 1 > 2 – x (do 7 > 1).
(*)
Mà – 1 < x < 2 nên x + 1 > 0, do đó (*) ⇔ x2 – x – 1 > 0 .
Kết hợp với điều kiện ta được .
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 15:
22/07/2024Giải các bất phương trình sau:
b) 2log(2x + 1) > 3.
 Xem đáp án
Xem đáp án
b) 2log(2x + 1) > 3
Điều kiện: 2x + 1 > 0 ⇔ x > .
Bất phương trình đã cho tương đương với
.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là .
Câu 16:
22/07/2024Áp suất khí quyển p (tính bằng kilôpascan, viết tắt là kPa) ở độ cao h (so với mực nước biển, tính bằng km) được tính theo công thức sau:
.
(Theo britannica.com)
a) Tính áp suất khí quyển ở độ cao 4 km.
 Xem đáp án
Xem đáp án
a) Ở độ cao 4 km, tức h = 4, thay vào công thức đã cho ta được
.
Vậy áp suất khí quyển ở độ cao 4 km khoảng 56,47 kPa.
Câu 17:
23/07/2024b) Ở độ cao trên 10 km thì áp suất khí quyển sẽ như thế nào?
 Xem đáp án
Xem đáp án
b) Ở độ cao trên 10 km, tức h > 10, khi đó ta có
.
Vậy ở độ cao trên 10 km thì áp suất khí quyển nhỏ hơn 23,97 kPa.
Câu 18:
23/07/2024Giải các phương trình sau:
a) 3x – 1 = 27;
 Xem đáp án
Xem đáp án
a) 3x – 1 = 27
⇔ 3x – 1 = 33
⇔ x – 1 = 3
⇔ x = 4
Vậy phương trình đã cho có nghiệm duy nhất là x = 4.
Câu 19:
22/07/2024Giải các phương trình sau:
b) ;
 Xem đáp án
Xem đáp án
b)
⇔ 4x2 – 6 = – 2x2 + 18
⇔ 6x2 = 24
⇔ x2 = 4
⇔ x = ± 2.
Vậy tập nghiệm của phương trình đã cho là S = {– 2; 2}.
Câu 20:
22/07/2024Giải các phương trình sau:
c) ;
 Xem đáp án
Xem đáp án
c)
.
Vậy phương trình đã cho có nghiệm duy nhất là .
Câu 21:
22/07/2024Giải các phương trình sau:
d) 5x = 32x – 1.
 Xem đáp án
Xem đáp án
d) 5x = 32x – 1
Lấy lôgarit cơ số 3 hai vế của phương trình ta được
log35x = log332x – 1
⇔ x log35 = 2x – 1
⇔ (2 – log35)x = 1
⇔ x = .
Vậy phương trình đã cho có nghiệm duy nhất là x = .
Câu 22:
22/07/2024Giải các phương trình sau:
a) log(x + 1) = 2;
 Xem đáp án
Xem đáp án
a) log(x + 1) = 2
Điều kiện: x + 1 > 0 ⇔ x > – 1.
Phương trình đã cho tương đương với x + 1 = 102 ⇔ x = 100 – 1 ⇔ x = 99 (t/m).
Vậy phương trình đã cho có nghiệm duy nhất x = 99.
Câu 23:
22/07/2024 Xem đáp án
Xem đáp án
b) 2log4x + log2(x – 3) = 2
Điều kiện: .
Ta có 2log4x + log2(x – 3) = 2
⇔ log2x + log2(x – 3) = 2
⇔ log2x(x – 3) = 2
⇔ x(x – 3) = 22
⇔ x2 – 3x – 4 = 0
⇔ x = – 1 hoặc x = 4.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 4.
Câu 24:
22/07/2024Giải các phương trình sau:
c) lnx + ln(x – 1) = ln4x;
 Xem đáp án
Xem đáp án
c) lnx + ln(x – 1) = ln4x
Điều kiện: .
Ta có: lnx + ln(x – 1) = ln4x
⇔ lnx(x – 1) = ln4x
⇔ x(x – 1) = 4x
⇔ x2 – 5x = 0
⇔ x(x – 5) = 0
⇔ x = 0 hoặc x = 5.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 5.
Câu 25:
19/07/2024Giải các phương trình sau:
d) log3(x2 – 3x + 2) = log3(2x – 4).
 Xem đáp án
Xem đáp án
d) log3(x2 – 3x + 2) = log3(2x – 4)
Điều kiện: .
Phương trình đã cho tương đương với
x2 – 3x + 2 = 2x – 4
⇔ x2 – 5x + 6 = 0
⇔ x = 2 hoặc x = 3.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 3.
Câu 26:
22/07/2024Giải các bất phương trình sau:
a) 0,12 – x > 0,14 + 2x;
 Xem đáp án
Xem đáp án
a) 0,12 – x > 0,14 + 2x
⇔ 2 – x < 4 + 2x (do 0 < 0,1 < 1)
⇔ 3x > – 2
⇔ x > .
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 27:
22/07/2024Giải các bất phương trình sau:
b) 2 . 52x + 1 ≤ 3;
 Xem đáp án
Xem đáp án
b) 2 . 52x + 1 ≤ 3
.
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 28:
16/07/2024Giải các bất phương trình sau:
c) log3(x + 7) ≥ – 1;
 Xem đáp án
Xem đáp án
c) log3(x + 7) ≥ – 1
Điều kiện: x + 7 > 0 ⇔ x > – 7.
Ta có: log3(x + 7) ≥ – 1
⇔ x + 7 ≥ 3– 1
⇔ x ≥
.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là .
Câu 29:
21/07/2024Giải các bất phương trình sau:
d) log0,5(x + 7) ≥ log0,5(2x – 1).
 Xem đáp án
Xem đáp án
d) log0,5(x + 7) ≥ log0,5(2x – 1)
Điều kiện: .
Ta có: log0,5(x + 7) ≥ log0,5(2x – 1)
⇔ x + 7 ≤ 2x – 1 (do 0 < 0,5 < 1)
⇔ x ≥ 8.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là S = [8; + ∞).
Câu 30:
22/07/2024Bác Minh gửi tiết kiệm 500 triệu đồng ở một ngân hàng với lãi suất không đổi 7,5% một năm theo thể thức lãi kép kì hạn 12 tháng. Tổng số tiền bác Minh thu được (cả vốn lẫn lãi) sau n năm là:
A = 500 ∙ (1 + 0,075)n (triệu đồng).
Tính thời gian tối thiểu gửi tiết kiệm để bác Minh thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
 Xem đáp án
Xem đáp án
Số tiền bác Minh nhận được sau n năm gửi tiết kiệm là
A = 500 ∙ (1 + 0,075)n = 500 ∙ 1,075n (triệu đồng).
Để có được 800 triệu đồng thì A = 800
⇔ 500 ∙ 1,075n = 800 ⇔ 1,075n = 1,6 ⇔ n = log1,0751,6 ≈ 6,5.
Vậy sau khoảng 7 năm gửi tiết kiệm thì bác An thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
Câu 31:
22/07/2024Số lượng vi khuẩn ban đầu trong một mẻ nuôi cấy là 500 con. Người ta lấy một mẫu vi khuẩn trong mẻ nuôi cấy đó, đếm số lượng vi khuẩn và thấy rằng tỉ lệ tăng trưởng vi khuẩn là 40% mỗi giờ. Khi đó số lượng vi khuẩn N(t) sau t giờ nuôi cấy được ước tính bằng công thức sau:
N(t) = 500e0,4t.
Hỏi sau bao nhiêu giờ nuôi cấy, số lượng vi khuẩn vượt mức 80 000 con?
 Xem đáp án
Xem đáp án
Số lượng vi khuẩn vượt mức 80 000 con khi N(t) > 80 000
⇔ 500e0,4t > 80 000 ⇔ e0,4t > 160 ⇔ 0,4t > ln160 ⇔ t > ≈ 12,69.
Vậy sau khoảng 12,69 giờ nuôi cấy, số lượng vi khuẩn vượt mức 80 000 con.
Câu 32:
22/07/2024Giả sử nhiệt độ T (℃) của một vật giảm dần theo thời gian cho bởi công thức: T = 25 + 70e– 0,5t, trong đó thời gian t được tính bằng phút.
a) Tìm nhiệt độ ban đầu của vật.
 Xem đáp án
Xem đáp án
a) Nhiệt độ ban đầu T0 của vật ứng với nhiệt độ tại thời điểm t = 0, từ đó ta được
T0 = 25 + 70e– 0,5 ∙ 0 = 95 (℃).
Vậy nhiệt độ ban đầu của vật là 95 ℃.
Câu 33:
22/07/2024b) Sau bao lâu nhiệt độ của vật còn lại 30 ℃.
 Xem đáp án
Xem đáp án
b) Nhiệt độ của vật còn lại 30 ℃, tức T = 30, khi đó t thỏa mãn phương trình
25 + 70e– 0,5t = 30 .
Vậy sau khoảng 5,28 phút nhiệt độ của vật còn lại 30 ℃.
Câu 34:
22/07/2024Tính nồng độ ion hydrogen (tính bằng mol/lít) của một dung dịch có độ pH là 8.
 Xem đáp án
Xem đáp án
Ta có: pH = – log[H+] = 8. Suy ra [H+] = 10– 8 (mol/lít).
Vậy nồng độ ion hydrogen của dung dịch có độ pH là 8 là 10– 8 mol/lít.
