Giải SGK Toán 11 CTST Bài 2. Hai đường thẳng song song
Giải SGK Toán 11 CTST Bài 2. Hai đường thẳng song song
-
90 lượt thi
-
21 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
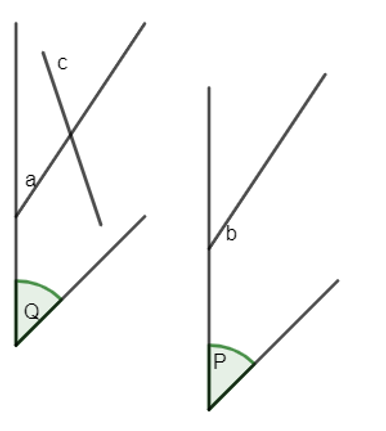
19/07/2024Mô tả vị trí giữa các cặp đường thẳng a và b, b và c, c và d có trong hình bên

 Xem đáp án
Xem đáp án
Sau khi học xong bài học này ta có thể trả lời được câu hỏi trên là:
+) Đường thẳng a và b là hai đường thẳng chéo nhau.
+) Đường thẳng b và c là hai đường thẳng song song.
+) Đường thẳng c và d là hai đường thẳng đồng phẳng.
Câu 2:
21/07/2024a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng a, b cùng nằm trong một mặt phẳng.
 Xem đáp án
Xem đáp án
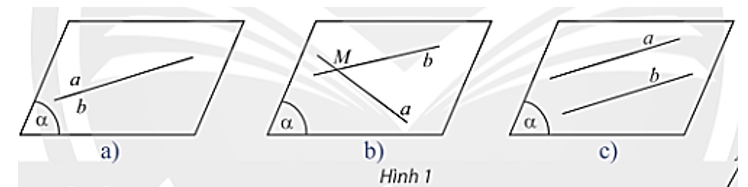
a) Các trường hợp có thể xảy ra đối với hai đường thẳng a và b cùng nằm trong một mặt phẳng là:
+) Hình 1a): Hai đường thẳng a và b trùng nhau.
+) Hình 1b): Hai đường thẳng a và b cắt nhau tại một điểm M.
+) Hình 1c): Hai đường thẳng a và b song song.
Câu 3:
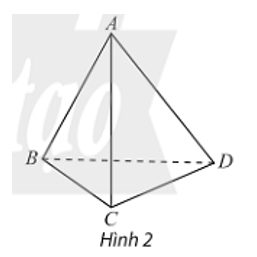
16/07/2024b) Cho tứ diện ABCD. Hai đường thẳng AB và CD có cùng nằm trong bất kì mặt phẳng nào không?
 Xem đáp án
Xem đáp án
b) Hai đường thẳng AB và CD không cùng nằm trong một mặt phẳng nào cả.
Câu 4:
23/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) AB và CD;
b) SA và SC;
c) SA và BC.
 Xem đáp án
Xem đáp án
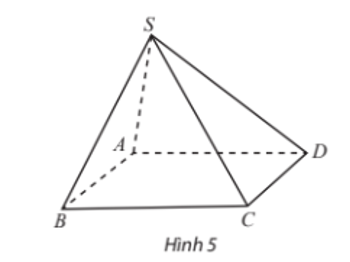
a) Trong mặt phẳng (ABCD) có nên AB // CD (vì ABCD là hình bình hành).
b) Trong mặt phẳng (SAC) có: SA cắt SC tại S.
c) Giả sử SA và BC cùng nằm trong mặt phẳng (P).
Suy ra (P) chưa bốn đỉnh của tứ diện SABC. Điều này là vô lí.
Vậy SA và BC không nằm trong bất kì mặt phẳng nào, suy ra SA và BC chéo nhauCâu 5:
19/07/2024Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

 Xem đáp án
Xem đáp án

+) Hai đường thẳng a và b nằm trong mặt phẳng phía trên của cầu sắt và song song với nhau.
+) Hai đường thẳng c và d nằm trong mặt phẳng phía trên của cầu sắt và cắt nhau tại điểm A.
+) Hai đường thẳng e và f không cùng nằm trong một mặt phẳng nên e và f là hai đường thẳng chéo nhau.
Câu 6:
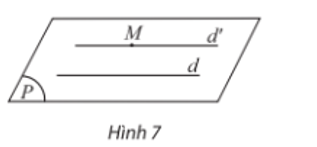
22/07/2024a) Trong không gian, cho điểm M ở ngoài đường thẳng d. Đặt (P) = mp(M, d). Trong (P), qua M vẽ đường thẳng d’ song song với d, đặt (Q) = mp(d, d’). Có thể khẳng định hai mặt phẳng (P) và (Q) trùng nhau không?
 Xem đáp án
Xem đáp án
a) Ta có:
(P) = mp(M, d) nên (P) xác định duy nhất.
(Q) = mp(d, d’), mà M ∈ d’ nên (Q) = mp(M, d). Do đó (P) và (Q) trùng nhau.
Câu 7:
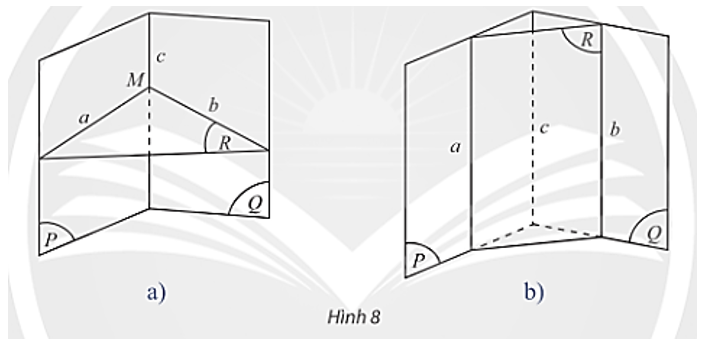
22/07/2024b) Cho ba mặt phẳng (P), (Q), (R) cắt nhau theo ba giao tuyến a, b, c phân biệt với a = (P) ∩ (R); b = (Q) ∩ (R); c = (P) ∩ (Q) (Hình 8).
Nếu a và b có điểm chung M thì điểm M có thuộc c không?
 Xem đáp án
Xem đáp án
b) Ta có:
Mà c = (P) ∩ (Q) nên M ∈ c.
Câu 8:
22/07/2024Cho hình chóp S.ABCD. Vẽ hình thang ADMS có hai đáy là AD và MS. Gọi d là đường thẳng trong không gian đi qua S và song song với AD. Chứng minh đường thẳng d nằm trong mặt phẳng (SAD).
 Xem đáp án
Xem đáp án
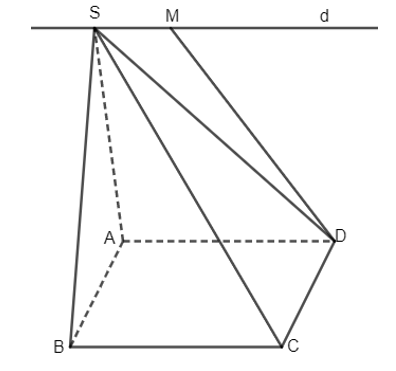
Ta có ADMS là hình thang nên SM // AD
Do trong không gian chỉ có duy nhất một đường thẳng đi qua S và song song với AD nên SM phải trùng với d.
Mà SM ⊂ (SAD)
Do đó d ⊂ (SAD).
Câu 9:
20/07/2024Ta đã biết trong cùng một mặt phẳng, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau (Hình 13a).
Trong không gian, cho ba đường thẳng a, b, c không đồng phẳng, a và b cùng song song với c. Gọi M là điểm thuộc a, d là giao tuyến của mp(a, c) và mp(M, b) (Hình 13b). Do b // c nên ta có d//b và d//c. Giải thích tại sao d phải trùng với a. Từ đó, nêu kết luận về vị trí giữa a và b.

 Xem đáp án
Xem đáp án
Ta có: mp(a, c) = mp(M, c) và mp(a, b) = mp(m, b)
Mà d là giao tuyến của mp(a, c) và mp(M, b)
Suy ra M ∈ d
Ta lại có d//b và d//c
Do đó d phải trùng a.
Câu 10:
19/07/2024Cho tứ diện ABCD có I và J lần lượt là trung điểm của các cạnh BC và BD. Gọi (P) là mặt phẳng đi qua I, J và cắt hai cạnh AC và AD lần lượt tại M và N.
a) Chứng minh IJNM là một hình thang.
 Xem đáp án
Xem đáp án
a) Ta có: .
Xét tứ giác IJNM có: MN // IJ nên IJNM là hình thang.
Câu 11:
22/07/2024b) Tìm vị trí của điểm M để IJNM là hình bình hành.
 Xem đáp án
Xem đáp án
b) Để IJNM là hình bình hành thì MN = IJ
Ta có: IJ = CD (IJ là đường trung bình của tam giác BCD) nên MN = CD và MN // CD nên MN là đường trung bình của tam giác ACD. Khi đó M là trung điểm của AC.
Câu 12:
12/07/2024Một chiếc lều (Hình 16a) được minh họa như Hình 16b.
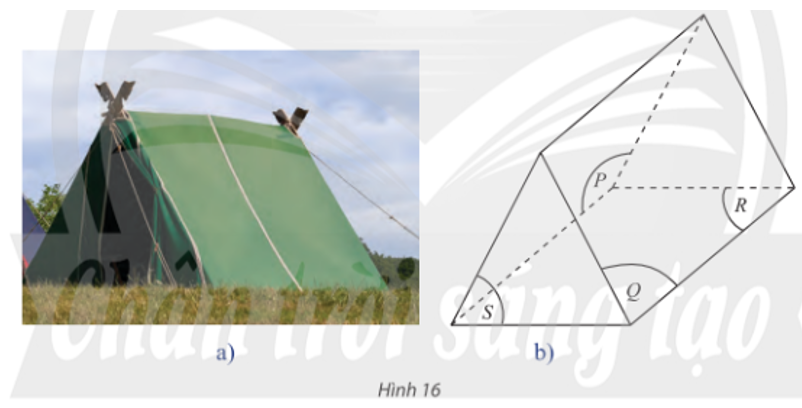
a) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song.
b) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy.
 Xem đáp án
Xem đáp án
a) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song là (P), (Q) và (R).
b) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy là:
(P), (S) và (R) hoặc (Q), (S) và (R).
Câu 13:
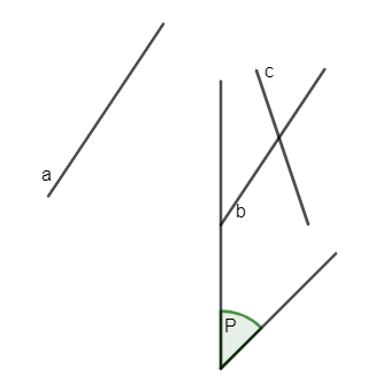
19/07/2024Cho hai đường thẳng song song a và b. Mệnh đề sau đây đúng hay sai?
a) Đường thẳng c cắt a thì cũng cắt b.
 Xem đáp án
Xem đáp án
a) Mệnh đề: “Hai đường thẳng a và b song song, đường thẳng c cắt a thì c cũng cắt b” là một mệnh đề sai vì c và b cũng có thể chéo nhau (không đồng phẳng).
Câu 14:
14/07/2024b) Đường thẳng c chéo với a thì cũng chéo với b.
 Xem đáp án
Xem đáp án
b) Mệnh đề: “Hai đường thẳng a và b song song, đường thẳng c chéo với a thì cũng chéo với b là một mệnh đề sai.
Câu 15:
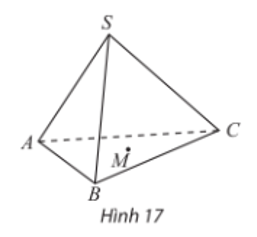
17/07/2024Hình chóp S.ABC và điểm M thuộc miền trong tam giác ABC (Hình 17). Qua M, vẽ đường thẳng d song song với SA, cắt (SBC). Trên hình vẽ, hãy chỉ rõ vị trí của điểm N và xác định giao tuyến của hai mặt phẳng (SAC) và (CMN).
 Xem đáp án
Xem đáp án
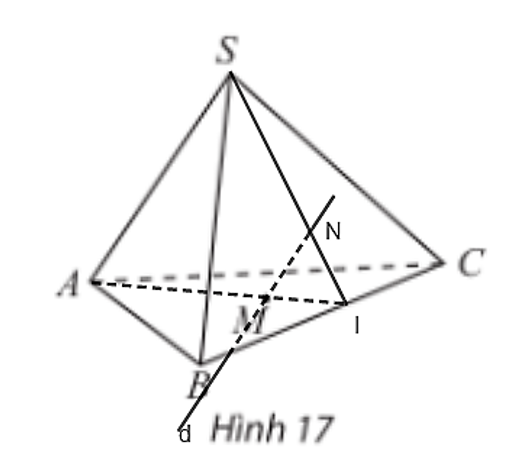
+) Trong mặt phẳng (ABC) kéo dài AM cắt cạnh BC tại I.
Ta có: mp(d, SA) = mp(SAI)
Trong mặt phẳng (SAI) gọi N là giao điểm của SI và d mà SI ⊂ (SBC). Do đó giao điểm của đường thẳng d và (SBC) là N.
Gọi d’ là giao tuyến của hai mặt phẳng (SAC) và (CMN).
Ta có:
Mà
Do đó C ∈ d’.
Vậy giao tuyến của hai mặt phẳng (SAC) và (CMN) là đường thẳng d’ đi qua C và song song với SA.
Câu 16:
06/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của hai mặt phẳng (SCD) và (SAB).
 Xem đáp án
Xem đáp án
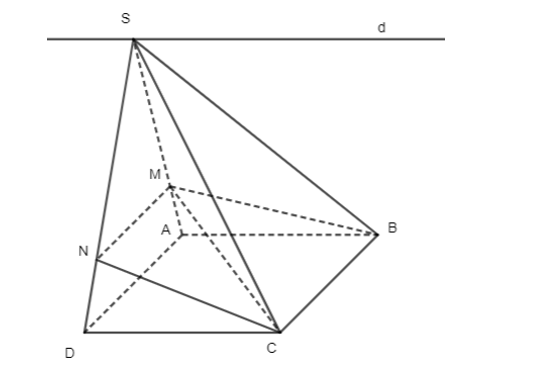
a) Ta có: CD // AB
CD ⊂ (SCD), AB ⊂ (SAB)
S ∈ (SAB) ∩ (SCD)
Do đó giao tuyến của hai mặt phẳng (SCD) và (SAB) là đường thẳng d đi qua S và song song với AB và CD.
Câu 17:
23/07/2024b) Lấy một điểm M trên đoạn SA (M khác S và A), mặt phẳng (BCM) cắt SD tại N. Tứ giác CBMN là hình gì?
 Xem đáp án
Xem đáp án
b) Trong mặt phẳng (SAD), kẻ đường thằng qua M song song với AD cắt SD tại N.
Mà AD // BC nên MN // BC.
Do đó mp(M, BC) = mp(MN, BC).
Vậy N là giao điểm của SD với (MBC).
Câu 18:
21/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm của SD. Hai mặt phẳng (IAC) và (SBC) cắt nhau theo giao tuyến Cx. Chứng minh rằng Cx // SB.
 Xem đáp án
Xem đáp án
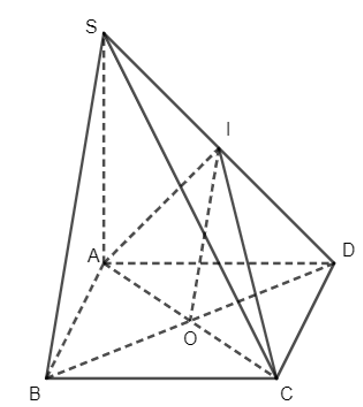
Gọi O là giao điểm của AC và BD
Ta có: .Câu 19:
20/07/2024Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng ICD cắt SA, SB lần lượt tại M, N.
a) Hãy nói cách xác định hai điểm M và N. Cho AB = a. Tính MN theo a.
 Xem đáp án
Xem đáp án
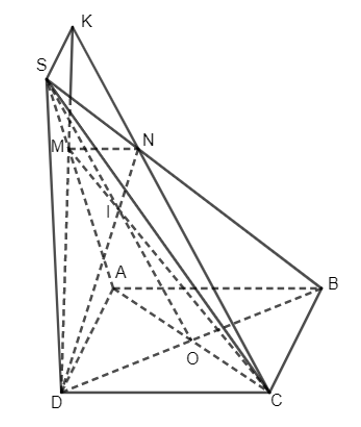
a) +) Trong mặt phẳng (SBD) có DI cắt SB tại N.
Mà DI ⊂ (ICD)
Do đó (ICD) cắt SB tại N.
+) Trong mặt phẳng (SAC) có CI cắt SA tại M.
Mà CI ⊂ (ICD)
Do đó (ICD) cắt SA tại M.
+)
Câu 20:
06/07/2024b) Trong mặt phẳng (CDMN), gọi K là giao điểm của CN và DM. Chứng minh SK // BC //AD.
 Xem đáp án
Xem đáp án
b) Ta có:
(SAD) ∩ (ABCD) = AD
(SBC) ∩ (ABCD) = BC
(SAD) ∩ (SBC) = SK
Mà AD // BC
⇒ SK // AD // BC.
Câu 21:
11/07/2024Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một ví dụ khác về các đường thẳng song song trong thực tế.

 Xem đáp án
Xem đáp án
Hình 18a) các sợi dây cáp điện đồng phẳng và là các đường thẳng song song.
Hình 18b) các đường bờ ruộng là các đường thẳng song song.
Hình 18c) các đường rìa của mỗi bậc thang là các đường thẳng song song.
Hình 18d) các rìa phím của mỗi phím đàn là các đường thẳng song song.
Hình 18e) các rìa mỗi kệ của tủ là các đường thẳng song song.
Hình 18g) mỗi hàng gạch tạo ra một đường thẳng và các đường thẳng này song song với nhau.
