Giải SGK Toán 11 Cánh diều Bài 2. Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
Giải SGK Toán 11 Cánh diều Bài 2. Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
-
150 lượt thi
-
22 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất một lần (Hình 1).

Xét các biến cố ngẫu nhiên:
A: “Mặt xuất hiện của xúc xắc có số chấm là số chẵn”;
B: “Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 3”;
C: “Mặt xuất hiện của xúc xắc có số chấm là số chẵn hoặc chia hết cho 3”.
Biến cố C có liên hệ như thế nào với hai biến cố A và B?
 Xem đáp án
Xem đáp án
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có C = A ∪ B.
Câu 2:
23/07/2024Xét phép thử “Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất một lần”. Gọi Ω là không gian mẫu của phép thử đó. Xét hai biến cố A và B nêu trong bài toán ở phần mở đầu.
a) Viết các tập con A, B của tập hợp Ω tương ứng với các biến cố A, B.
b) Đặt C = A ∪ B. Phát biểu biến cố C dưới dạng mệnh đề nêu sự kiện.
 Xem đáp án
Xem đáp án
a) Khi gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất một lần thì ta có không gian mẫu là Ω = {1; 2; 3; 4; 5; 6};
Biến cố A: “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” có tập hợp những kết quả thuận lợi là A = {2; 4; 6};
Biến cố B: “Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 3” có tập hợp những kết quả thuận lợi là B = {1; 3; 5}.
b) Ta có C = A ∪ B = {1; 2; 3; 4; 5; 6}.
Phát biểu dưới dạng mệnh đề nêu sự kiện của biến cố C là: “Mặt xuất hiện của xúc xắc có số chấm là số chẵn hoặc chia hết cho 3”.
Câu 3:
23/07/2024Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3,…,12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Phát biểu biến cố A ∪ B dưới dạng mệnh đề nêu sự kiện.
 Xem đáp án
Xem đáp án
Phát biểu dưới dạng mệnh đề nêu sự kiện của biến cố A ∪ B là: “Số xuất hiện trên thẻ rút ra là số chia hết cho 3 hoặc chia hết cho 4”.
Câu 4:
15/07/2024Đối với các tập hợp A, B trong Hoạt động 1, ta đặt D = A ∩ B. Phát biểu biến cố D dưới dạng mệnh đề nêu sự kiện.
 Xem đáp án
Xem đáp án
Phát biểu dưới dạng mệnh đề nêu sự kiện của biến cố A ∩ B là: “Số xuất hiện trên thẻ rút ra vừa là số chẵn vừa là số chia hết cho 3”.
Câu 5:
23/07/2024Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Xét các biến cố A: “Số chấm xuất hiện ở lần thứ nhất là số lẻ” và B: “Số chấm xuất hiện ở lần thứ hai là số lẻ”. Phát biểu biến cố A ∩ B dưới dạng mệnh đề nêu sự kiện.
 Xem đáp án
Xem đáp án
Phát biểu dưới dạng mệnh đề nêu sự kiện của biến cố A ∩ B là: “Số chấm xuất hiện ở cả hai lần gieo đều là số lẻ”.
Câu 6:
23/07/2024Xét phép thử “Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp”.
Gọi Ω là không gian mẫu của phép thử đó. Xét các biến cố:
A: “Số chấm xuất hiện ở lần gieo thứ nhất là số lẻ”;
B: “Số chấm xuất hiện ở lần gieo thứ nhất là số chẵn”.
a) Viết các tập con A, B của không gian mẫu Ω tương ứng với các biến cố A, B.
b) Tìm tập hợp A ∩ B.
 Xem đáp án
Xem đáp án
Ω = {(x; y)| 1 ≤ x, y ≤ 6; x, y ∈ ℕ}.
a) A = {(x; y)| x là số lẻ; 1 ≤ x, y ≤ 6; x, y ∈ ℕ}.
B = {(x; y)| x là số chẵn; 1 ≤ x, y ≤ 6; x, y ∈ ℕ}.
b) A ∩ B = ∅.
Câu 7:
22/07/2024Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Hai biến cố sau có xung khắc không?
A: “Tổng số chấm trong hai lần gieo nhỏ hơn 5”;
B: “Tổng số chấm trong hai lần gieo lớn hơn 6”.
 Xem đáp án
Xem đáp án
Ta có: A = {2; 3; 4} và B = {7; 8; 9; 10; 11; 12}.
Do đó A ∩ B = ∅.
Vậy A và B là hai biến cố xung khắc.
Câu 8:
17/07/2024Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:
A: “Đồng xu xuất hiện mặt S ở lần gieo thứ nhất”;
B: “Đồng xu xuất hiện mặt N ở lần gieo thứ hai”.
Đối với hai biến cố A và B, hãy cho biết một kết quả thuận lợi cho biến cố này có ảnh hưởng gì đến xác xuất xảy ra của biến cố kia hay không.
 Xem đáp án
Xem đáp án
Ta có Ω = {(N; S); (N; N); (S; N); (S; S)}, n(Ω) = 4.
A = {(S; N); (S; S)} nên n(A) = 2. Do đó
B = {(N; N); (S; N)} nên n(B) = 2. Do đó
Câu 9:
19/07/2024Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Xét các biến cố sau:
A: “Số chấm xuất hiện ở lần gieo thứ nhất là số nguyên tố”;
B: “Số chấm xuất hiện ở lần gieo thứ hai là hợp số”.
Hai biến cố A và B có độc lập không? Có xung khắc không? Vì sao?
 Xem đáp án
Xem đáp án
− Ta có Ω = {(x; y)| 1 ≤ x, y ≤ 6; x, y ∈ ℕ}, do đó n(Ω) = 6.6 = 36.
⦁ A = {(x; y)| x là số nguyên tố; 1 ≤ x, y ≤ 6; x, y ∈ ℕ}
A = {(2; 1); (2; 2); …; (2; 6); (3; 1); (3; 2); ...; (3; 6); (5; 1); (5; 2); …; (5; 6)}, nên n(A) = 18.
⦁ B = {(x; y)| y là số hợp tố; 1 ≤ x, y ≤ 6; x, y ∈ ℕ}
B = {(1; 4); (2; 4); …; (6; 4); (1; 6); (2; 6); ...; (6; 6)}, nên n(B) = 12.
Xác suất của biến cố A khi biến cố B xảy ra bằng Xác suất của biến cố A khi biến cố B không xảy ra cũng bằng Do đó việc xảy ra hay không xảy ra của biến cố B không làm ảnh hưởng đến xác suất xảy ra của biến cố A. Mặt khác xác suất của biến cố B bằng không phụ thuộc vào việc xảy ra hay không xảy ra của biến cố A.
− Ta có kết quả (2; 4) là kết quả thuận lợi cho cả hai biến cố A và B nên A ∩ B ≠ ∅. Do đó biến cố A và B không là hai biến cố xung khắc.
Câu 10:
23/07/2024Chọn ngẫu nhiên một số nguyên dương không vượt quá 20. Xét biến cố A: “Số được viết ra là số chia hết cho 2” và biến cố B: “Số được viết ra là số chia hết cho 7”.
a) Tính P(A), P(B), P(A ∪ B) và P(A ∩ B).
b) So sánh P(A ∪ B) và P(A) + P(B) – P(A ∩ B).
 Xem đáp án
Xem đáp án
Không gian mẫu của phép thử chọn ngẫu nhiên một số nguyên dương không vượt quá 20 là: Ω = {1; 2; 3; …; 20}, n(Ω) = 20.
Tập hợp các kết quả thuận lợi của biến cố A là A = {2; 4; 6; …; 18; 20}, n(A) = 10.
Tập hợp các kết quả thuận lợi của biến cố B là B = {7; 14}, n(B) = 2.
Khi đó A ∪ B = {2; 4; 6; 7; 8; 10; 12; 14; 16; 18; 20}, n(A ∪ B) = 11.
A ∩ B = {14}, n(A ∩ B) = 1.
a)
và
b) Ta có
Câu 11:
21/07/2024Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 7” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 11”. Tính P(A ∪ B).
 Xem đáp án
Xem đáp án
Không gian mẫu của phép thử trên là Ω = {1; 2; 3; …; 52}, n(Ω) = 52.
Tập hợp các kết quả thuận lợi cho biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 7” là A = {7; 14; 21; 28; 35; 42; 49}, n(A) = 7. Do đó
Tập hợp các kết quả thuận lợi cho biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 11” là B = {11; 22; 33; 44}, n(B) = 4. Do đó
Trong các số 1; 2; 3; …; 52, không có số nào chia hết cho cả 7 và 11 nên A, B là hai biến cố xung khắc.
Do đó
Câu 12:
30/06/2024Xét các biến cố độc lập A và B trong Ví dụ 4.
a) Tính P(A), P(B) và P(A ∩ B).
b) So sánh P(A ∩ B) và P(A).P(B).
 Xem đáp án
Xem đáp án
a) Số phần tử của không gian mẫu là nên n(Ω) = 49.
Số kết quả thuận lợi cho biến cố A là nên n(A) = 21.
Số kết quả thuận lợi cho biến cố B là nên n(B) = 28.
Ta có và
Số kết quả thuận lợi cho cả hai biến cố A và B là nên n(A ∩ B) = 12. Do đó
b) Ta có
Câu 13:
20/07/2024Một xưởng sản xuất có hai máy chạy độc lập với nhau. Xác suất để máy I và máy II chạy tốt lần lượt là 0,8 và 0,9. Tính xác suất của biến cố C: “Cả hai máy của xưởng sản xuất đều chạy tốt”.
 Xem đáp án
Xem đáp án
Xét biến cố A: “Máy I của xưởng sản xuất chạy tốt”, ta có P(A) = 0,8.
Xét biến cố B: “Máy II của xưởng sản xuất chạy tốt”, ta có P(A) = 0,9.
Ta thấy A, B là hai biến cố độc lập và C = A ∩ B nên ta có:
P(C) = P(A ∩ B) = P(A).P(B) = 0,8.0,9 = 0,72.
Câu 14:
15/07/2024Cho hai đường thẳng song song d1 và d2. Trên d1 lấy 17 điểm phân biệt, trên d2 lấy 20 điểm phân biệt. Chọn ngẫu nhiên 3 điểm, tính xác suất để các điểm này tạo thành 3 đỉnh của một tam giác.
 Xem đáp án
Xem đáp án
⦁ Tất cả có 17 + 20 = 37 điểm phân biệt nằm trên hai đường thẳng d1 và d2. Mỗi cách chọn 3 điểm trong 37 điểm là một tổ hợp chập 3 của 37 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 3 của 37 và
⦁ Xét các biến cố:
H: “Ba đỉnh của tam giác là 3 điểm của cả hai đường thẳng d1 và d2”.
A: “Trong ba đỉnh của tam giác có 1 điểm thuộc d1, 2 điểm thuộc d2”
B: “Trong ba đỉnh của tam giác có 2 điểm thuộc d1, 1 điểm thuộc d2”.
Khi đó H = A ∪ B và A ∩ B = ∅.
Do hai biến cố A và B xung khắc nên n(H) = n(A) + n(B).
Số kết quả thuận lợi cho biến cố A là:
Số kết quả thuận lợi cho biến cố B là:
Số các kết quả thuận lợi cho biến cố H là:
n(H) = n(A) + n(B) = 3 230 + 2 720 = 5 950.
⦁ Vậy xác suất của biến cố H là:
Câu 15:
16/07/2024Để trang trí một tờ giấy có dạng hình chữ nhật, bạn Thuỳ chia tờ giấy đó thành bốn hình chữ nhật nhỏ bằng nhau. Mỗi hình chữ nhật nhỏ được tô bằng một trong hai màu xanh hoặc vàng. Vẽ sơ đồ hình cây biểu thị các khả năng mà bạn Thuỳ có thể tô màu trang trí cho tờ giấy đó.
 Xem đáp án
Xem đáp án
Sơ đồ cây biểu thị các khả năng mà bạn Thuỳ có thể tô màu trang trí cho tờ giấy đó như sau:
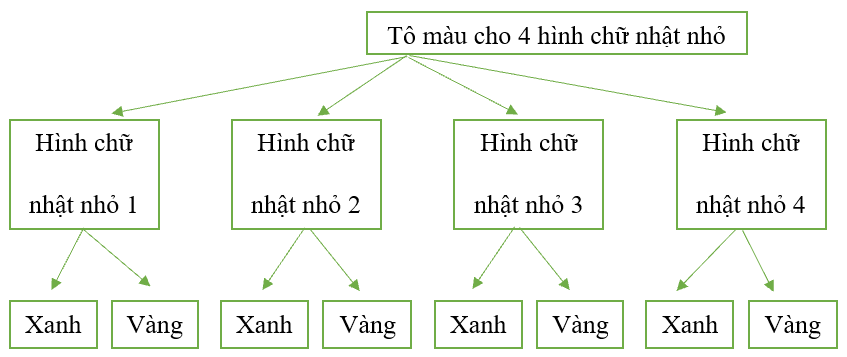
Câu 16:
21/07/2024Một hộp có 5 viên bi màu xanh, 6 viên bi màu đỏ và 7 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi trong hộp. Tính xác suất để 5 viên bi được chọn có đủ ba màu và số bi màu đỏ bằng số bi màu vàng.
 Xem đáp án
Xem đáp án
⦁ Mỗi cách chọn ra đồng thời 5 viên bi trong hộp có 5 + 6 + 7 = 18 viên bi cho ta một tập hợp chập 5 của 18 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 5 của 18 phần tử và
⦁ Xét biến cố A: “Chọn được 5 viên bi có đủ ba màu và số bi màu đỏ bằng số bi màu vàng”.
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố A:

Như vậy, số kết quả thuận lợi cho biến cố A là: n(A) = 1 575 + 420 = 1 995.
Vậy xác suất của biến cố A là:
Câu 17:
21/07/2024Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:
A: “Lần thứ nhất xuất hiện mặt ngửa”;
B : “Lần thứ hai xuất hiện mặt ngửa”;
C: “Cả hai lần đều xuất hiện mặt ngửa”;
D : “Có ít nhất một lần xuất hiện mặt ngửa”.
Trong hai biến cố C, D biến cố nào là biến cố hợp của hai biến cố A, B? Biến cố nào là biến cố giao của hai biến cố A, B?
 Xem đáp án
Xem đáp án
⦁ Biến cố hợp của hai biến cố A và B là biến cố mà lần thứ nhất hoặc lần thứ hai tung đồng xu xuất hiện mặt ngửa, tức là “Có ít nhất một lần xuất hiện mặt ngửa”. Vậy biến cố D là biến cố hợp của A và B.
⦁ Biến cố giao của hai biến cố A và B là biến cố mà cả hai lần đều xuất hiện mặt ngửa. Do đó biến cố C: “Cả hai lần đều xuất hiện mặt ngửa” là biến cố hợp của A và B.
Câu 18:
18/07/2024Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:
A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 4”;
B: “Số chấm xuất hiện ở lần gieo thứ hai nhỏ hơn 4”;
C: “Số chấm xuất hiện ở lần gieo thứ nhất nhỏ hơn 4”.
Trong các biến cố trên, hãy:
a) Tìm cặp biến cố xung khắc;
b) Tìm cặp biến cố độc lập.
 Xem đáp án
Xem đáp án
a) Cặp biến cố xung khắc là A và C, vì nếu A xảy ra thì C không thể xảy ra, và ngược lại, nếu C xảy ra thì A không thể xảy ra.
b) Cặp biến cố độc lập là A và B, vì xảy ra hay không xảy ra biến cố A không ảnh hưởng đến khả năng xảy ra biến cố B, và ngược lại, xảy ra hay không xảy ra biến cố B cũng không ảnh hưởng đến khả năng xảy ra biến cố A.
Tương tự, các cặp biến cố A và C, B và C cũng là biến cố độc lập.
Vậy các biến cố độc lập là: A và B; A và C; B và C.
Câu 19:
25/11/2024Chọn ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của biến cố M: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11 hoặc chia hết cho 12”.
 Xem đáp án
Xem đáp án
Lời giải
Ta có: Ω = {10; 11; 12; …; 99}.
Không gian mẫu của phép thử có phần tử, tức là n(Ω) = 90.
Xét các biến cố:
M: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11 hoặc chia hết cho 12”.
A: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11”;
B: “Số tự nhiên có hai chữ số được viết ra chia hết cho 12”;
Khi đó M = A ∪ B và A ∩ B = ∅
Do hai biến cố A và B xung khắc nên n(M) = n(A ∪ B) = n(A) + n(B).
Số các kết quả thuận lợi cho biến cố A là n(A) = 9.
Số các kết quả thuận lợi cho biến cố B là n(B) = 8.
Số các kết quả thuận lợi cho biến cố M là: n(M) = 9 + 8 = 17.
Suy ra
*Phương pháp giải:
- Sử dụng quy tắc chỉnh hợp để tìm ra phần tử của không gian mẫu.
- Sử dụng quy tắc liệt kê để liệt kê các phần tử của tập hợp M.
*Lý thuyết:
1. Xác suất của biến cố
– Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố.
Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:
P(A) =
Trong đó n(A) và n() lần lượt là kí hiệu số phần tử của tập A và .
Chú ý:
+ Định nghĩa trên được gọi là định nghĩa cổ điển của xác suất.
+ Với mọi biến cố A, 0 ≤ P(A) ≤ 1.
+ P() = 1, P(∅) = 0.
+ Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 1.
2. Tính xác suất bằng sơ đồ hình cây
– Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đồ hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất
Xem thêm
Lý thuyết Xác suất của biến cố – Toán 10 Chân trời sáng tạo
Câu 20:
16/07/2024Một hộp có 12 viên bi có cùng kích thước và khối lượng, trong đó có 7 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi từ hộp đó. Tính xác suất để trong 5 viên bi được chọn có ít nhất 2 viên bi màu vàng.
 Xem đáp án
Xem đáp án
− Mỗi cách chọn ra đồng thời 5 viên bi trong hộp có 12 viên bi cho ta một tổ hợp chập 5 của 12 phần tử. Do đó, không gian mẫu gồm các tổ hợp chập 5 của 12 phần tử và
− Xét biến cố A: “Trong 5 viên bi được chọn có ít nhất 2 viên bi màu vàng”.
Khi đó biến cố đối của biến cố A là : “Trong 5 viên bi không có viên bi màu vàng hoặc có 1 viên bi màu vàng”.
⦁ Trường hợp 1: Trong 5 viên bi không có viên bi màu vàng.
Có cách chọn.
⦁ Trường hợp 1: Trong 5 viên bi có 1 viên bi màu vàng.
Có cách chọn.
Như vậy, số kết quả thuận lợi cho biến cố là:
Suy ra
Do đó
Câu 21:
17/07/2024Hai bạn Việt và Nam cùng tham gia một kì thi trắc nghiệm môn Toán và môn Tiếng Anh một cách độc lập nhau. Đề thi của mỗi môn gồm 6 mã đề khác nhau và các môn khác nhau thì mã đề cũng khác nhau. Đề thi được sắp xếp và phát cho học sinh một cách ngẫu nhiên. Tính xác suất để hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó.
 Xem đáp án
Xem đáp án
− Chọn 1 mã đề thi trong 6 mã đề thi môn Toán cho bạn Việt có 6 cách.
Chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh cho bạn Việt có 6 cách.
Chọn 1 mã đề thi trong 6 mã đề thi môn Toán cho bạn Nam có 6 cách.
Chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh cho bạn Nam có 6 cách.
Do đó không gian mẫu của phép thử có số phần tử là 64, tức là n(Ω) = 64.
− Gọi A là biến cố: “Hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó”.
⦁ Trường hợp 1: Hai bạn trùng mã đề thi môn Toán, không trùng mã đề thi môn Tiếng Anh.
Bạn Việt chọn 1 mã đề thi trong 6 mã đề thi môn Toán có 6 cách; chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh có 6 cách.
Bạn Nam chọn 1 mã đề thi môn Toán trùng với mã đề thi bạn Việt đã cho có 1 cách; chọn 1 mã đề thi trong 5 mã đề thi môn Tiếng Anh (trừ mã đề thi bạn Việt đã chọn) có 5 cách.
Như vậy, có 6.6.1.5 = 180 cách.
⦁ Trường hợp 2: Hai bạn trùng mã đề thi môn Tiếng Anh, không trùng mã đề thi môn Toán.
Tương tự trường hợp 1, cũng có 6.1.6.5 = 180 cách.
Như vậy, số kết quả thuận lợi cho biến cố A là: n(A) = 180 + 180 = 360.
Vậy xác suất của biến cố A là:
Câu 22:
23/07/2024Trong một chiếc hộp có 20 viên bi có cùng kích thước và khối lượng, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có đúng hai màu.
 Xem đáp án
Xem đáp án
− Mỗi cách chọn ra đồng thời 3 viên bi trong hộp có 20 viên bi cho ta một tổ hợp chập 3 của 20 phần tử. Do đó, không gian mẫu Ω của phép thử trên gồm các tổ hợp chập 3 của 20 phần tử và
− Xét biến cố A: “3 viên bi lấy ra có đúng hai màu”.
Khi đó biến cố đối của A là: “3 viên bi lấy ra có 3 màu khác nhau hoặc có cùng màu”.
⦁ Trường hợp 1: Ba viên bi lấy ra có 3 màu khác nhau.
Có cách chọn.
⦁ Trường hợp 1: Ba viên bi lấy ra có cùng màu (cùng màu đỏ hoặc cùng màu xanh hoặc cùng màu vàng).
Có cách chọn.
Như vậy, số kết quả thuận lợi cho biến cố là:
Do đó, xác suất của biến cố đối là:
Vậy xác suất của biến cố A là:
