Giải SBT Vật lý 11 KNTT Vận tốc, gia tốc trong dao động điều hoà
Giải SBT Vật lý 11 KNTT Vận tốc, gia tốc trong dao động điều hoà
-
54 lượt thi
-
11 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Chọn kết luận đúng về dao động điều hoà của con lắc lò xo.
A. Quỹ đạo là đường hình sin.
B. Quỹ đạo là một đoạn thẳng.
C. Vận tốc tỉ lệ thuận với thời gian.
D. Gia tốc tỉ lệ thuận với thời gian.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
A – sai vì quỹ đạo là đoạn thẳng.
C, D – sai vì vận tốc và gia tốc biến thiên điều hoà theo thời gian.Câu 2:
11/07/2024Một vật dao động điều hoà có phương trình \(x = 2{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}} \right)\). Phương trình vận tốc của vật là:
A. \(v = 5{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
B. \(v = 10{\rm{cos}}\left( {5t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
C. \(v = 20{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
D. \(v = 5{\rm{cos}}\left( {5t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Phương trình vận tốc \(v = x' = 2.5\cos \left( {5t - \frac{\pi }{6} + \frac{\pi }{2}} \right) = 10\cos \left( {5t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right)\)
Câu 3:
07/07/2024Vận tốc của một vật dao động điều hoà tại vị trí cân bằng là \(1{\rm{\;cm}}/{\rm{s}}\) và gia tốc của vật tại vị trí biên là \(1,57{\rm{\;cm}}/{{\rm{s}}^2}\). Chu kì dao động của vật là:
A. 3,24 s.
B. \(6,28{\rm{\;s}}\).
C. \(4{\rm{\;s}}\).
D. \(2{\rm{\;s}}\).
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vận tốc của vật tại vị trí cân bằng là \({v_{{\rm{max}}}} = \omega A\); gia tốc của vật tại vị trí biên là: \({a_{{\rm{max}}}} = {\omega ^2}A\) \( \Rightarrow \omega = \frac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = 1,57{\rm{rad}}/{\rm{s}};T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{1,57}} = 4{\rm{\;s}}\).
Câu 4:
21/07/2024Một chất điểm dao động điều hoà với tần số \(4{\rm{\;Hz}}\) và biên độ \(10{\rm{\;cm}}\). Gia tốc cực đại của chất điểm là:
A. \(2,5{\rm{\;m}}/{{\rm{s}}^2}\).
B. \(25{\rm{\;m}}/{{\rm{s}}^2}\).
C. \(63,1{\rm{\;m}}/{{\rm{s}}^2}\).
D. \(6,31{\rm{\;m}}/{{\rm{s}}^2}\).
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gia tốc cực đại \({a_{{\rm{max}}}} = {\omega ^2}A = {(2\pi f)^2}A = {\left( {2\pi .4} \right)^2}.0,1 \approx 63,1{\rm{\;m/}}{{\rm{s}}^{\rm{2}}}\).
Câu 5:
07/07/2024Chất điểm \(M\) chuyển động tròn đều trên một đường tròn với tốc độ dài \(160{\rm{\;cm}}/{\rm{s}}\) và tốc độ góc \(4{\rm{rad}}/{\rm{s}}\). Hình chiếu \({\rm{P}}\) của \({\rm{M}}\) trên một đường thẳng cố định nằm trong mặt phẳng hình tròn dao động điều hoà với biên độ và chu kì lần lượt là:
A. \(40{\rm{\;cm}};0,25{\rm{\;s}}\).
B. \(40{\rm{\;cm}};1,57{\rm{\;s}}\).
C. \(40{\rm{\;m}};0,25{\rm{\;s}}\).
D. \(2,5{\rm{\;m}};0,25{\rm{\;s}}\). Xem đáp án
Xem đáp án
Đáp án đúng là B
Biên độ \(A = \frac{{{v_{{\rm{max}}}}}}{\omega } = \frac{{160}}{4} = 40{\rm{\;cm}}\); chu kì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{4} = 1,57{\rm{\;s}}\).
Câu 6:
04/07/2024Phương trình vận tốc của một vật dao động là: \(v = 120{\rm{cos}}20t\left( {{\rm{cm}}/{\rm{s}}} \right)\), đơn vị đo của thời gian \(t\) là giây. Vào thời điểm \(t = \frac{T}{6}\) (T là chu kì dao động), vật có li độ là:
A. \(3{\rm{\;cm}}\).
C. \(3\sqrt 3 {\rm{\;cm}}\).
D. \( - 3\sqrt 3 {\rm{\;cm}}\).
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Từ phương trình vận tốc, ta suy ra phương trình li độ: \(x = 6{\rm{cos}}\left( {20t - \frac{\pi }{2}} \right)\left( {{\rm{cm}}} \right)\).
Khi \(t = \frac{T}{6} \Rightarrow x = 6{\rm{cos}}\left( {\frac{\pi }{3} - \frac{\pi }{2}} \right) = 6{\rm{cos}}\left( { - \frac{\pi }{6}} \right) = 3\sqrt 3 \left( {cm} \right)\).
Câu 7:
28/06/2024Một chất điểm dao động điều hoà. Biết li độ và vận tốc của chất điểm tại thời điểm \({t_1}\) lần lượt là \({x_1} = 3{\rm{\;cm}}\) và \({v_1} = - 60\sqrt 3 {\rm{\;cm}}/{\rm{s}}\); tại thời điểm \({{\rm{t}}_2}\) lần lượt là \({x_2} = 3\sqrt 2 {\rm{\;cm}}\) và \({v_2} = 60\sqrt 2 {\rm{\;cm}}/{\rm{s}}\). Biên độ và tần số góc của dao động lần lượt là:
A. \(6{\rm{\;cm}};20{\rm{rad}}/{\rm{s}}\).
B. \(6{\rm{\;cm}};12{\rm{rad}}/{\rm{s}}\).
C. \(12{\rm{\;cm}};20{\rm{rad}}/{\rm{s}}\).
D. \(12{\rm{\;cm}};10{\rm{rad}}/{\rm{s}}\).
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Thiết lập và áp dụng công thức: \(\left\{ \begin{array}{l}\frac{{x_1^2}}{{{A^2}}} + \frac{{v_1^2}}{{{\omega ^2}{A^2}}} = 1\\\frac{{x_2^2}}{{{A^2}}} + \frac{{v_2^2}}{{{\omega ^2}{A^2}}} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x_1^2{\omega ^2} + v_1^2 = {\omega ^2}{A^2}\\x_2^2{\omega ^2} + v_2^2 = {\omega ^2}{A^2}\end{array} \right.\)
\( \Rightarrow \omega = \sqrt {\frac{{v_2^2 - v_1^2}}{{x_1^2 - x_2^2}}} = \sqrt {\frac{{{{2.60}^2} - {{3.60}^2}}}{{9 - 2.9}}} = 20\,\,{\rm{rad/s}}{\rm{.}}\)
\( \Rightarrow A = \sqrt {x_1^2 + \frac{{v_1^2}}{{{\omega ^2}}}} = \sqrt {{3^2} + \frac{{3 \cdot {{60}^2}}}{{{{20}^2}}}} = 6\;{\rm{cm}}.\)
Câu 8:
14/07/2024Một dao động điều hoà trên đoạn thẳng dài \(10{\rm{\;cm}}\) và thực hiện được 50 dao động trong thời gian \(78,5{\rm{\;s}}\). Tìm vận tốc và gia tốc của vật khi đi qua vị trí có li độ \(x = - 3{\rm{\;cm}}\) theo chiều hướng về vị trí cân bằng?
 Xem đáp án
Xem đáp án
\(A = 5{\rm{\;cm}};T = \frac{{78,5}}{{50}} = 1,57{\rm{\;s}};\omega = \frac{{2\pi }}{T} = 4{\rm{rad/s}}\).
Khi \(x = - 3{\rm{\;cm}}\) thì gia tốc \(a = - {\omega ^2}x = 48{\rm{\;cm/}}{{\rm{s}}^{\rm{2}}}\).
\(v = \pm \omega \sqrt {{A^2} - {x^2}} = \pm 4\sqrt {{5^2} - {3^2}} = \pm 16{\rm{\;cm/s}}{\rm{.\;}}\)
Vì vật có li độ âm, đang hướng về vị trí cân bằng nên \(v > 0\). Vậy \(v = 16{\rm{\;cm}}/{\rm{s}}\).
Câu 9:
20/07/2024Một vật dao động điều hoà với tần số góc \(\omega = 5{\rm{rad}}/{\rm{s}}\). Khi \({\rm{t}} = 0\), vật đi qua vị trí có li độ \(x = - 2{\rm{\;cm}}\) và có vận tốc \(10{\rm{\;cm}}/{\rm{s}}\) hướng về vị trí biên gần hơn. Hãy viết phương trình dao động của vật.
 Xem đáp án
Xem đáp án
Áp dụng công thức: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 \Rightarrow A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 2} \right)}^2} + \frac{{{{10}^2}}}{{{5^2}}}} = 2\sqrt 2 {\rm{\;cm}}{\rm{.\;}}\)
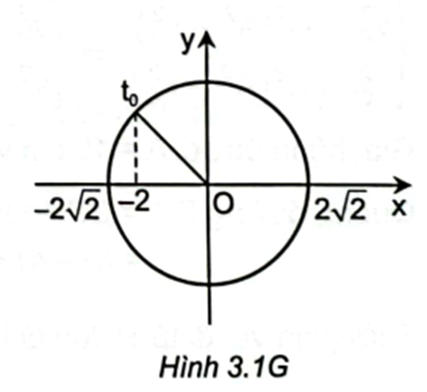
Theo đề bài khi \({\rm{t}} = 0\) thì: \(x = - 2{\rm{\;cm}} = - \frac{{A\sqrt 2 }}{2} < 0\) và có chiều hướng về vị trí biên gần nhất (Hình 3.1G) nên \(\varphi = \frac{{3\pi }}{4}\).
Phương trình dao động: \(x = 2\sqrt 2 {\rm{cos}}\left( {5t + \frac{{3\pi }}{4}} \right)\left( {{\rm{cm}}} \right).\)
Câu 10:
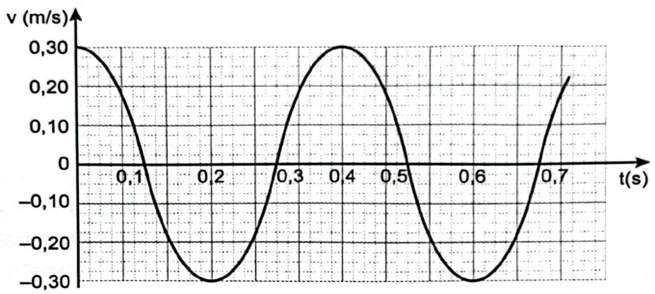
23/07/2024Hình 3.1 mô tả sự biến thiên vận tốc theo thời gian của một vật dao động điều hoà.
Hình 3.1
 Xem đáp án
Xem đáp án
Từ đồ thị ta xác định được:
\({\rm{T}} = 0,4{\rm{\;s}} \Rightarrow \omega = \frac{{2\pi }}{{\rm{T}}} = \frac{{2\pi }}{{0,4}} = 5\pi \left( {{\rm{rad}}/{\rm{s}}} \right);{v_{{\rm{max}}}} = 0,3{\rm{\;m}}/{\rm{s}}\).
Khi \({\rm{t}} = 0\) thì \({\rm{v}} = {{\rm{v}}_{{\rm{max}}}}\)\( \Rightarrow \varphi = 0\), vậy phương trình vận tốc theo thời gian là: \(v = 0,3{\rm{cos}}5\pi {\rm{t}}\left( {{\rm{m/s}}} \right)\).
Câu 11:
25/06/2024Hình 3.1 mô tả sự biến thiên vận tốc theo thời gian của một vật dao động điều hoà.

Hình 3.1
Viết phương trình li độ và gia tốc theo thời gian.
 Xem đáp án
Xem đáp án
Phương trình li độ: \(x = 1,91{\rm{cos}}\left( {5\pi t - \frac{\pi }{2}} \right)\left( {{\rm{cm}}} \right)\).
Phương trình gia tốc: \(a = - {\omega ^2}x = 4,71{\rm{cos}}\left( {5\pi t + \frac{\pi }{2}} \right)\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).
Có thể bạn quan tâm
Các bài thi hot trong chương
- Trắc nghiệm Vật lí 11 KNTT Bài 1: Dao động điều hòa (444 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 4: Bài tập về giao động điều hòa (281 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 2: Mô tả dao động điều hòa (265 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 5: Động năng. Thế năng. Sự chuyển hóa giữa động năng và thế năng trong dao động điều hòa (262 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 7: Bài tập về chuyển hóa năng lượng trong dao động điều hòa (252 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 6: Dao động tắt dần. Dao động cưỡng bức (238 lượt thi)
