Giải SBT Vật lý 11 KNTT Dao động tắt dần. Dao động cưỡng bức. Hiện tượng cộng hưởng
Giải SBT Vật lý 11 KNTT Dao động tắt dần. Dao động cưỡng bức. Hiện tượng cộng hưởng
-
65 lượt thi
-
9 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Tìm phát biểu sai. Dao động tắt dần là dao động có
A. tần số giảm dần theo thời gian.
B. cơ năng giảm dần theo thời gian.
C. biên độ dao động giảm dần theo thời gian.
D. ma sát và lực cản càng lớn thì dao động tắt dần càng nhanh.
Xem đáp án
Đáp án đúng là A
Dao động tắt dần là dao động có biên độ, cơ năng giảm dần theo thời gian, khi ma sát và lực cản càng lớn thì dao động tắt dần càng nhanh.
Câu 2:
22/07/2024Trong dao động tắt dần, một phần cơ năng đã biến đổi thành
A. điện năng.
B. nhiệt năng.
C. hoá năng.
D. quang năng.
Xem đáp án
Đáp án đúng là B
Trong dao động tắt dần, một phần cơ năng đã biến đổi thành nhiệt năng.
Câu 3:
19/07/2024Một con lắc lò xo đang dao động tắt dần, sau ba chu kì đầu tiên, biên độ của nó giảm đi \(10{\rm{\% }}\). Phần trăm cơ năng còn lại sau khoảng thời gian đó là
A. \(81{\rm{\% }}\).
B. \(6,3{\rm{\% }}\).
C. \(19{\rm{\% }}\).
D. \(27{\rm{\% }}\).
Xem đáp án
Đáp án đúng là A
Theo đề bài: \(\frac{{A - {A_3}}}{A} = 10{\rm{\% }} \Rightarrow \frac{{{A_3}}}{A} = 90{\rm{\% }} \Rightarrow \frac{{{W_3}}}{W} = {\left( {\frac{{{A_3}}}{A}} \right)^2} = 0,{9^2} = 0,81 = 81{\rm{\% }}\)
Câu 4:
19/07/2024Một con lắc lò xo dao động tắt dần theo phương ngang với chu kì \({\rm{T}} = 0,2{\rm{\;s}}\), lò xo nhẹ, vật nhỏ dao động có khối lượng \(100{\rm{\;g}}\). Hệ số ma sát giữa vật và mặt phẳng ngang là 0,01. Độ giảm biên độ của vật sau mỗi lần vật đi từ biên này tới biên kia là
A. \(0,02{\rm{\;mm}}\).
B. \(0,04{\rm{\;mm}}\).
C. \(0,2{\rm{\;mm}}\).
D. \(0,4{\rm{\;mm}}\).
Xem đáp án
Đáp án đúng là C
Nguyên nhân của dao động tắt dần là do lực cản của môi trường, trong bài toán này là lực ma sát. Độ giảm cơ năng sau một nửa chu kì bằng công của lực ma sát thực hiện trong chu kì đó, ta có:
\(\frac{1}{2}m{\omega ^2}{A^2} - \frac{1}{2}m{\omega ^2}{A^{{\rm{'}}2}} = {F_{ms}}\left( {A + A'} \right) \Leftrightarrow \frac{1}{2}m{\omega ^2}\left( {A + A'} \right)\left( {A - A'} \right) = {F_{ms}}\left( {A + A'} \right)\)
\(\; \Rightarrow {\rm{\Delta }}A = \frac{{2{F_{ms}}}}{k} = \frac{{2\mu mg}}{k}\)
Độ giảm biên độ sau mỗi lần qua vị trí cân bằng:
\(\frac{{{\rm{\Delta A}}}}{2} = \frac{{2\mu {\rm{mg}}}}{{\rm{k}}} = \frac{{2 \cdot 0,01 \cdot 0,1 \cdot 10}}{{100}} = 0,2 \cdot {10^{ - 3}}{\rm{\;m}}.\)
Câu 5:
22/07/2024Một người xách một xô nước đi trên đường, mỗi bước đi dài \({\rm{L}} = 50{\rm{\;cm}}\) thì nước trong xô bị sóng sánh mạnh nhất. Tốc độ đi của người đó là v = 2,5 km/h. Chu kì dao động riêng của nước trong xô là
A. \(1,44{\rm{\;s}}\).
B. \(0,35{\rm{\;s}}\).
C. \(0,45{\rm{\;s}}\).
D. 0,52 s. Xem đáp án
Đáp án đúng là A
Hai bước đi là một chu kì. Chu kì dao động riêng của nước trong xô là:
\({\rm{T}} = \frac{{2L}}{{{\rm{\;V}}}} = \frac{{2 \cdot 0,5}}{{0,69}} \approx 1,44{\rm{\;s}}{\rm{.\;}}\)
Câu 6:
10/07/2024Một con lắc lò xo gồm lò xo có khối lượng không đáng kể. Chu kì dao động của con lắc là \(0,1\pi \left( {\rm{s}} \right)\). Con lắc dao động cưỡng bức theo phương trùng với trục của lò xo dưới tác dụng của ngoại lực tuần hoàn \(F = {F_0}{\rm{cos}}\omega t\left( N \right)\). Khi \(\omega \) lần lượt là \(10{\rm{rad}}/{\rm{s}}\) và \(15{\rm{rad}}/{\rm{s}}\) thì biên độ dao động tương ứng của con lắc lần lượt là \({A_1}\) và \({A_2}\). Hãy so sánh \({A_1}\) và \({A_2}\).
Xem đáp án
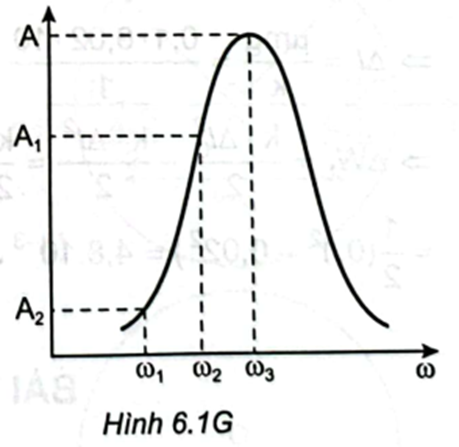
Khi xảy ra hiện tượng cộng hưởng: \({\omega _0} = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,1\pi }} = 20{\rm{rad}}/{\rm{s}}\)
Vì \({\omega _1} = 10{\rm{rad/s}}\) xa vị trí cộng hưởng hơn \({\omega _2} = 15{\rm{rad}}/{\rm{s}}\left( {{\omega _1} < {\omega _2} < {\omega _0}} \right)\) nên \({A_1} < {A_2}\) (Hình 6.1G).
Câu 7:
01/07/2024Một con lắc lò xo gồm vật nhỏ khối lượng \({\rm{m}} = 0,2{\rm{\;kg}}\), lò xo nhẹ có độ cứng \({\rm{k}} = 20{\rm{\;N}}/{\rm{m}}\) dao động trên mặt phẳng nằm ngang. Hệ số ma sát trượt giữa vật và mặt phẳng nằm ngang là \(\mu = 0,01\). Từ vị trí lò xo không bị biến dạng, truyền cho vật vận tốc ban đầu có độ lớn \({v_0} = 1{\rm{\;m}}/{\rm{s}}\) dọc theo trục lò xo (lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\)). Tính độ lớn lực đàn hồi cực đại của lò xo trong quá trình dao động.
Xem đáp án
Độ lớn của lực đàn hồi sẽ đạt cực đại khi vật ra tới vị trí biên lần đầu tiên sau khi được truyền vận tốc \({v_0}\) (vì biên độ ở các lần sau sẽ không bằng được ở lần này). Công của lực ma sát trên đoạn biên độ A đầu tiên đó bằng độ giảm cơ năng khi vật đi từ vị trí ban đầu tới vị trí biên: \( - \mu {\rm{mgA}} = \frac{{k{A^2}}}{2} - \frac{{mv_0^2}}{2}\)
Thay số: \( - 0,01 \cdot 0,2 \cdot 10A = \frac{{20{A^2}}}{2} - \frac{{0,2 \cdot {1^2}}}{2} \Rightarrow 10{A^2} + 0,02A - 0,1 = 0\)
\( \Rightarrow A = 0,099m \Rightarrow {F_{{\rm{dhmax\;}}}} = kA = 20.0,099 = 1,98{\rm{\;N}}\).
Câu 8:
25/06/2024Một con lắc lò xo gồm vật nhỏ có khối lượng \({\rm{m}} = 0,03{\rm{\;kg}}\) và lò xo có độ cứng \({\rm{k}} = 1,5{\rm{\;N}}/{\rm{m}}\). Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục của lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là \(\mu = 0,2\). Ban đầu, giữ vật ở vị trí lò xo bị dãn một đoạn \({\rm{\Delta }}{l_0} = 15{\rm{\;cm}}\) rồi buông nhẹ để con lắc dao động tắt dần. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Tính tốc độ lớn nhất mà vật nhỏ đạt được trong quá trình dao động.
Xem đáp án
Vật đạt tốc độ lớn nhất tại vị trí O mà lực ma sát cân bằng với lực đàn hồi của lò xo, khi đó vật còn cách vị trí mà lò xo không biến dạng một đoạn \({\rm{\Delta }}l\) xác định bởi:
\(\mu {\rm{mg}} = {\rm{k}} \cdot {\rm{\Delta }}l \Rightarrow {\rm{\Delta }}l = \frac{{\mu {\rm{mg}}}}{{\rm{k}}} = \frac{{0,2 \cdot 0,03 \cdot 10}}{{1,5}} = 0,04{\rm{\;m}}{\rm{.\;}}\)
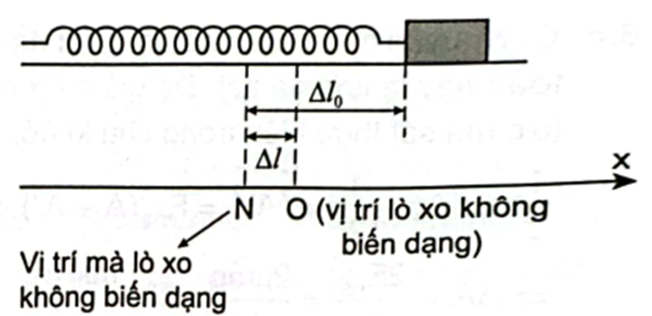
Công của lực ma sát trên đoạn \({\rm{\Delta }}{l_0} - {\rm{\Delta }}l\) đó bằng độ giảm cơ năng khi vật đi từ vị trí ban đầu tới vị trí cân bằng nói trên:
\[ - \mu {\rm{mg}}\left( {{\rm{\Delta }}{l_0} - {\rm{\Delta }}l} \right)\; = \frac{{{\rm{mv}}_{\max }^2}}{2} + \frac{{{\rm{k}} \cdot {\rm{\Delta }}{l^2}}}{2}\; - \frac{{{\rm{k}} \cdot {\rm{\Delta }}l_0^2}}{2}\]
Thay số: \( - 0,1 \cdot 0,03 \cdot 10\left( {0,15 - 0,04} \right) = \frac{{0,03v_{{\rm{max}}}^2}}{2} + \frac{{1,5 \cdot 0,{{04}^2}}}{2} - \frac{{1,5 \cdot 0,{{15}^2}}}{2}\)
Suy ra: \({v_{{\rm{max}}}} = 0,91{\rm{\;m}}/{\rm{s}} = 91{\rm{\;cm}}/{\rm{s}}\).
Câu 9:
20/07/2024Một con lắc lò xo gồm vật nhỏ khối lượng \({\rm{m}} = 0,02{\rm{\;kg}}\) và lò xo có độ cứng \({\rm{k}} = 1{\rm{\;N}}/{\rm{m}}\). Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là \(\mu = 0,1\). Ban đầu giữ vật ở vị trí lò xo bị nén \({\rm{\Delta }}{l_0} = 10{\rm{\;cm}}\) rồi buông nhẹ để con lắc dao động tắt dần. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Tính độ giảm thế năng của con lắc trong giai đoạn từ khi buông tới vị trí mà tốc độ dao động của con lắc cực đại lần đầu.
Xem đáp án
Vật đạt tốc độ lớn nhất \({v_{{\rm{max}}}}\) tại vị trí mà \({F_{ms}} = {F_{{\rm{oh\;}}}}\) (Hình 6.2G)
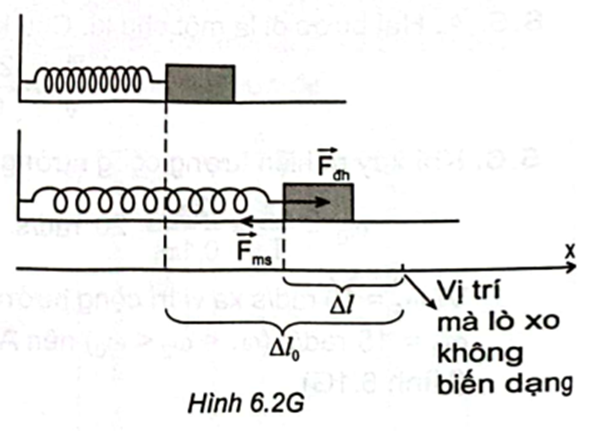
\( \Leftrightarrow \mu {\rm{mg}} = {\rm{k\Delta }}l\)
\( \Rightarrow {\rm{\Delta }}l = \frac{{\mu {\rm{mg}}}}{{\rm{k}}} = \frac{{0,1 \cdot 0,02 \cdot 10}}{1} = 0,02{\rm{\;m}}\).
\( \Rightarrow {\rm{\Delta }}{{\rm{W}}_{\rm{t}}} = \frac{{{\rm{k}} \cdot {\rm{\Delta }}l_0^2}}{2} - \frac{{{\rm{k}} \cdot {\rm{\Delta }}{l^2}}}{2} = \frac{{\rm{k}}}{2}\left( {{\rm{\Delta }}l_0^2 - {\rm{\Delta }}{l^2}} \right)\)\( = \frac{1}{2}\left( {0,{1^2} - 0,{{02}^2}} \right) = 4,8 \cdot {10^{ - 3}}{\rm{\;J}} = 4,8{\rm{\;mJ}}\)