a)  ${\log }_9\frac{1}{81}=lo{g}_9{\left(9\right)}^{-2} = -2$;                   

b) log 10 000 = log 10⁴ = 4;

c) log 0,001 = log(10)^{– 3} = – 3;               

d) log_0,7 1 = 0;

e) $lo{g}_5\sqrt[4]{5}={\log }_{{}_5}{\left(5\right)}^{\frac{1}{4}}=\frac{1}{4}$ ;                     

g) log_0,5 0,125 = log_0,5 0,5³ = 3.

a) $3^{{\log }_{3}5}=5$ ;                                       

b) e^{ln 3} = 3;                      

c) $7^{2{\log }_{7}8}={\left[7^{lo{g}_{7}8}\right]}^2=8^2=64$ ;                        

d) $2^{lo{g}_{2}3+{\log }_{2}5}=2^{lo{g}_{2}3}{.2}^{{\log }_{2}5}=3.5=15$ ;

e) $4^{lo{g}_2\left(\frac{1}{5}\right)}={\left(2^2\right)}^{lo{g}_2\left(\frac{1}{5}\right)}$

$={\left[2^{lo{g}_2\frac{1}{5}}\right]}^2={\left[\frac{1}{5}\right]}^2=\frac{1}{25}$

g) 0,001^{log 2} = ${\left({10}^{-3}\right)}^{log2}$   = ${\left({10}^{log2}\right)}^{-3}$ = $2^{-3}$  = $\frac{1}{8}$ .

a) ${\log }_8\frac{1}{32}=\frac{{\log }_2\frac{1}{32}}{{\log }_{2}8}=\frac{{\log }_2{2}^{-5}}{{\log }_2{2}^3}=-\frac{5}{3}$ ;

b) ${\log }_{5}3.{\log }_{3}5={\log }_{5}3\frac{1}{{\log }_{5}3}=1$ ;

c) $2^{\frac{1}{{\log }_{5}2}}=2^{lo{g}_{2}5}=5$ ;

d) ${\log }_{27}25.{\log }_{5}81=\frac{{\log }_{3}25}{{\log }_{3}27}\cdot \frac{{\log }_{3}81}{{\log }_{3}5}$

$=\frac{{\log }_3{5}^2}{{\log }_3{3}^3}\cdot \frac{{\log }_3{3}^4}{{\log }_{3}5}=\frac{2{\log }_{3}5}{3}\cdot \frac{4}{{\log }_{3}5}$$=\frac{8}{3}$

a) ${\log }_{3}5.{\log }_{5}7.{\log }_{7}9$  

$={\log }_{3}5.\frac{{\log }_{3}7}{{\log }_{3}5}.\frac{{\log }_{3}9}{{\log }_{3}7}$

b) ${\log }_2\frac{1}{25}.{\log }_3\frac{1}{32}.{\log }_5\frac{1}{27}={\log }_2{5}^{-2}.{\log }_3{2}^{-5}.{\log }_5{3}^{-3}$

<=> (–2) log₂ 5. (–5)log₃ 2. (–3) . (–3) log₅ 3

 <=> –30 log₂ 5 . log₂ 3 . log₅ 3 log₇ 21

$\iff -30{\log }_{2}5.\frac{{\log }_{2}2}{{\log }_{2}3}.\frac{{\log }_{2}3}{{\log }_{2}5}=-30$

a) log₇ 21 = 1,5646;

Ta nhập máy tính:            

Ta được kết quả:

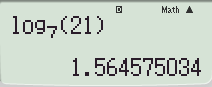
Làm tròn đến chữ số thập phân thứ tư 1,5646.

b) log 2,25 = 0,3522;     

Ta nhập máy tính:          

Ta được kết quả:

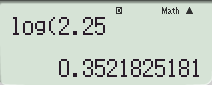
Làm tròn đến chữ số thập phân thứ tư 0,3522.

c) = 1,3195;

Ta nhập máy tính: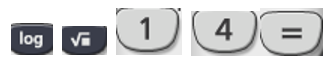      

Ta được kết quả:

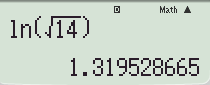
Làm tròn đến chữ số thập phân thứ tư 1,3195.

d) log_0,5 3 + log₅ 0,3 = –2,333.

Ta nhập máy tính:

Ta được kết quả:

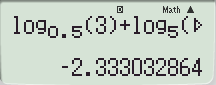
Làm tròn đến chữ số thập phân thứ tư – 2,333.

a) log_­2 45 = log₂ 3².5

= 2log₂ 3 + log₂ 5 = 2a + b;

b) ${\log }_2\frac{\sqrt{15}}{6}={\log }_2\sqrt{15}-{\log }_{2}6$$=\frac{1}{2}{\log }_{2}15-{\log }_2(2.3)$

$=\frac{1}{2}{\log }_2(3.5)-({\log }_{2}2+{\log }_{2}3)$$=\frac{1}{2}({\log }_{2}3+{\log }_{2}5)-(1+{\log }_{2}3)$

$=\frac{1}{2}(a+b)-(1+a)$$=-\frac{a}{2}+\frac{b}{2}-1$

c) ${\log }_{3}20=\frac{{\log }_{3}20}{{\log }_{2}3}$$=\frac{{\log }_2(2^2.5)}{{\log }_{3}3}$

$=\frac{2{\log }_{2}2+{\log }_{2}5}{{\log }_{2}3}$$=\frac{2+b}{a}$

a) log(xyz) = log x + log y + log z = a + b + c;

b) $\log \frac{x^3\sqrt[3]{y}}{100\sqrt{z}}=\log \left(x^3\sqrt[3]{y}\right)-\log \left(100\sqrt{z}\right)$

$=\log \left(x^3{y}^{\frac{1}{3}}\right)-\log \left({10}^2{z}^{\frac{1}{2}}\right)$$=3\log x+\frac{1}{3}\log y-2-\frac{1}{2}\log z$

$=3a+\frac{1}{3}b-\frac{1}{2}c-2$

c) ${\log }_z\left(x{y}^2\right)=\frac{\log \left(x{y}^2\right)}{\log z}$

$=\frac{\log xy+2\log }{\log z}=\frac{a+2b}{c}$