Giải SBT Toán 11 CTST Bài tập cuối chương 4
-
42 lượt thi
-
19 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm.
Xem đáp án
Đáp án đúng là: C
Yếu tố xác định một mặt phẳng duy nhất là hai đường thẳng cắt nhau.
Xét phương án A: Trường hợp ba điểm thẳng hàng không xác định được một mặt phẳng.
Xét phương án B: Trường hợp điểm nằm trên đường thẳng không xác định được một mặt phẳng.
Xét phương án D: Trường hợp bốn điểm không đồng phẳng không xác định được một mặt phẳng.
Câu 2:
11/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB và E là trung điểm của đoạn thẳng AB. Hình vẽ nào sau đây là hình biểu diễn của hình chóp S.ABCD ?
Xem đáp án
Đáp án đúng là: A
Câu 3:
23/07/2024Cho hình chóp S.ABCD có AC cắt BD tại M, AB cắt CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là giao tuyến của (SAC) và (SBD) ?
A. SM.
B. SN.
C. SB.
D. SC.
Xem đáp án
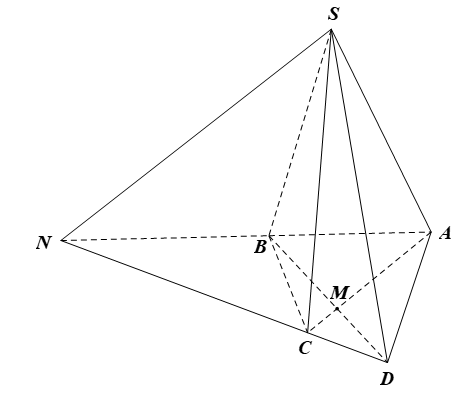
M ∈ AC mà AC ⊂ (SAC) nên M ∈ (SAC);
M ∈ BD mà BD ⊂ (SBD) nên M ∈ (SBD).
Do đó M ∈ (SAC) ∩ (SBD).
Lại có S ∈ (SAC) ∩ (SBD) nên (SAC) ∩ (SBD) = SM.
Câu 4:
06/07/2024Cho hình chóp S.ABCD, đáy là hình bình hành có O là giao điểm của AC và BD. Gọi M, N lần lượt là các điểm nằm trên cạnh SC và SD. Đường thẳng SO cắt đường thẳng AM và BN lần lượt tại P và Q. Giao điểm của đường thẳng AM với mặt phẳng (SBD) là điểm nào sau đây?
A. Điểm P.
B. Điểm Q.
C. Điểm O.
D. Điểm M.
Xem đáp án
Ta có AM ∩ SO = P, mà SO ⊂ (SBD) nên AM ∩ (SBD) = P.
Câu 5:
06/07/2024Trong không gian, hai đường thẳng không có điểm chung thì
A. cắt nhau.
B. chéo nhau hoặc song song.
C. chéo nhau.
D. song song.
Xem đáp án
Đáp án đúng là: B
Trong không gian, hai đường thẳng không có điểm chung và
⦁ và cùng nằm trong một mặt phẳng thì chúng song song với nhau;
⦁ và không cùng nằm trong một mặt phẳng thì chúng chéo nhau.
Câu 6:
17/07/2024Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?
A. Nếu a // (P) thì b // (P).
B. Nếu a cắt (P) thì b cắt (P).
C. Nếu a nằm trên (P) thì b // (P).
D. Nếu a nằm trên (P) thì b nằm trên (P).
Xem đáp án
Đáp án đúng là: B
⦁ a // b, a // (P) thì b // (P) hoặc b ⊂ (P);
⦁ a // b, a cắt (P) thì b cắt (P);
⦁ a // b, a ⊂ (P) thì b // (P) hoặc b ⊂ (P).
Vậy ta chọn phương án B.Câu 7:
10/07/2024Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP) là đường thẳng d. Khẳng định nào dưới đây đúng?
A. d đi qua trung điểm hai cạnh AB và CD.
B. d đi qua trung điểm hai cạnh AB và AD.
C. d là đường thẳng PQ.
D. d là đường thẳng QA.
Xem đáp án
Đáp án đúng là: A
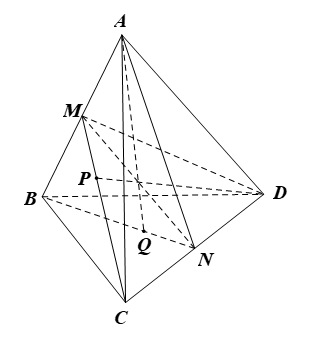
Gọi M, N lần lượt là trung điểm của AB, CD.
Ta có M ∈ AB mà AB ⊂ (ABQ), nên M ∈ (ABQ) (1)
Khi đó đường trung tuyến CM đi qua trọng tâm P của của ∆ABC.
Do đó mặt phẳng (DCP) chính là mặt phẳng (DCM), nên M ∈ (DCP) (2)
Từ (1) và (2) suy ra M ∈ (ABQ) ∩ (DCP).
Tương tự ta cũng có N ∈ (ABQ) ∩ (DCP).
Suy ra (ABQ) ∩ (DCP) = MN.
Câu 8:
16/07/2024Cho hình chóp tứ giác S.ABCD. Gọi M và N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
A. MN // (ABCD).
B. MN // (SAB).
C. MN // (SAD).
D. MN // (SCD).
Xem đáp án
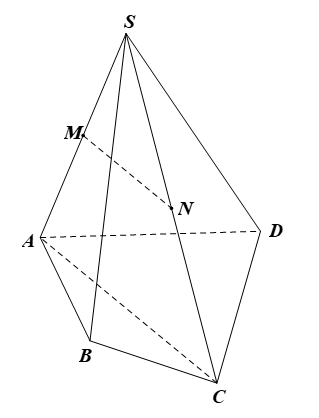
Xét ∆SAC có M và N lần lượt là trung điểm của SA và SC nên MN là đường trung bình của tam giác
Do đó MN // AC
Mà AC ⊂ (ABCD) nên MN // (ABCD).
Câu 9:
16/07/2024Cho đường thẳng a nằm trong mặt phẳng (α) và đường thẳng b nằm trong mặt phẳng (β). Biết (α) // (β). Trong các khẳng định sau, khẳng định nào sai?
A. a // (β).
B. b // (α).
C. a // b.
D. Nếu có một mặt phẳng (γ) chứa a và b thì a // b.
Xem đáp án
Đáp án đúng là: C
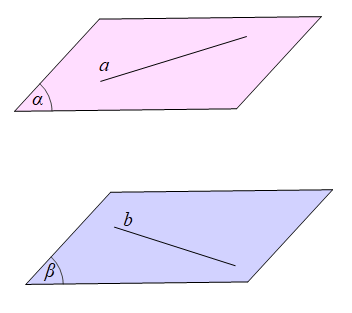
a ⊂ (α); b ⊂ (β) và (α) // (β) nên a // b.
Câu 10:
22/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây?
A. BD.
B. SC.
C. AC.
D. AB.
Xem đáp án
Đáp án đúng là: D
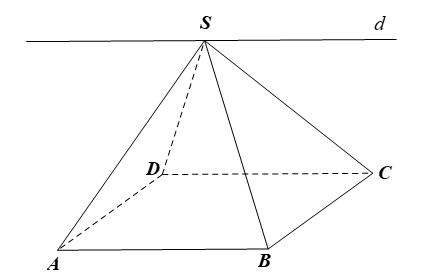
Do ABCD là hình bình hành nên AB // CD.
Lại có AB ⊂ (SAB), CD ⊂ (SCD) và S ∈ (SAB) ∩ (SCD)
Do đó (SAB) ∩ (SCD) = d với d là đường thẳng đi qua S và d // AB // CD.
Câu 11:
22/07/2024Cho hình bình hành ABCD. Từ các đỉnh A, B, C và D lần lượt kẻ các tia Ax, By, Cz và Dt song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt).
Xem đáp án
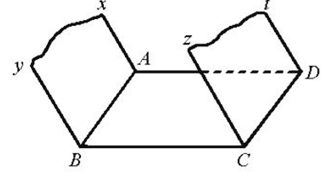
Ta có Cz // By nên Cz // (Ax, By).
Do tứ giác ABCD là hình bình hành nên CD // AB do đó CD // (Ax, By).
Khi đó Cz // (Ax, By);
CD // (Ax, By);
Cz ⊂ (Cz, Dt), CD ⊂ (Cz, Dt) và Cz ∩ CD = C.
Do đó (Cz, Dt) // (Ax, By).
Câu 12:
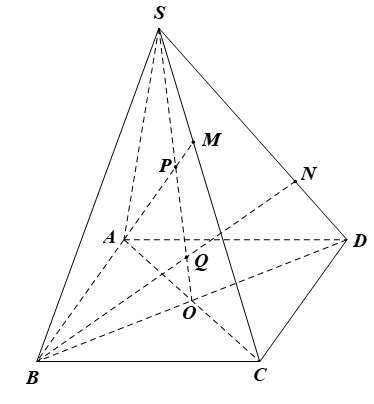
17/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của AC và BD. Gọi M, N, P lần lượt là ba điểm nằm trên các cạnh AB, BC, SO. Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp S.ABCD (nếu có).
Xem đáp án
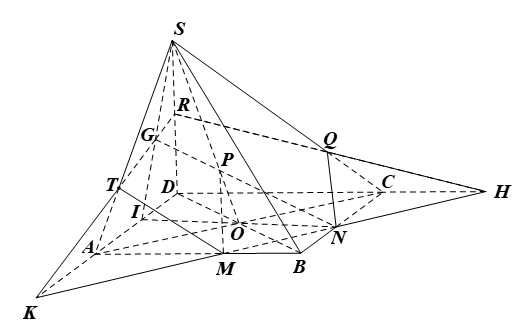
• Do M ∈ AB, N ∈ BC và AB ⊂ (ABCD), BC ⊂ (ABCD) nên MN ⊂ (ABCD)
Mà MN ⊂ (MNP)
Suy ra (MNP) ∩ (ABCD) = MN.
• Trong mặt phẳng (ABCD), gọi H là giao điểm của MN và DC; K là giao điểm của MN và AD; I là giao điểm của NO và AD.
Trong mặt phẳng (SIO), gọi G là giao điểm của NP và SI.
Trong mặt phẳng (SAD), gọi T là giao điểm của KG và SA và R là giao điểm của KG và SD.
Trong mặt phẳng (SDC), gọi Q là giao điểm của RH và SC.
Khi đó, (MNP) ∩ (SAB) = TM.
(MNP) ∩ (SBC) = NQ;
(MNP) ∩ (SDC) = QR;
(MNP) ∩ (SAD) = RT.
Câu 13:
06/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của SA. Tìm giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD, biết rằng (P) đi qua M, song song với SC và AD.
Xem đáp án
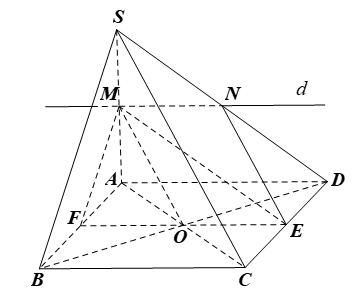
Gọi O là giao điểm của AC và BD, E là trung điểm của CD.
Xét ∆SAC có: M, O lần lượt là trung điểm của SA, AC nên MO là đường trung bình của ∆SAC, suy ra SC // MO.
Mà MO ⊂ (MOE), suy ra SC // (MOE).
Xét ∆ADC có: O, E lần lượt là trung điểm của AC, CD nên OE là đường trung bình của ∆ADC, suy ra AD // OE.
Mà OE ⊂ (MOE), suy ra AD // (MOE).
Khi đó, mặt phẳng (P) đã cho là (MOE).
Trong mặt phẳng (ABCD), gọi F là giao điểm của OE và AB.
Mà OE ⊂ (MOE), AB ⊂ (ABCD)
Suy ra (MOE) ∩ (ABCD) = EF, (MOE) ∩ (SAB) = FM.
Vì M ∈ (MOE) ∩ (SAD) và OE // AD
Nên (MOE) ∩ (SAD) = d, với d là đường thẳng đi qua M và d // AD // OE.
Trong mặt phẳng (SAD), d cắt SD tại N.
Do đó, (MOE) ∩ (SAD) = MN và (MOE) ∩ (SDC) = NE.
Vậy (MOE) ∩ (ABCD) = EF;
(MOE) ∩ (SAB) = FM;
(MOE) ∩ (SAD) = MN;
(MOE) ∩ (SDC) = NE.
Câu 14:
14/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và tam giác SAB đều. Gọi M là điểm thuộc cạnh BC sao cho BM = x (0 < x < a), mặt phẳng (α) đi qua M, song song với hai đường thẳng SA và AB.
a) Xác định giao tuyến của mặt phẳng (α) với các mặt của hình chóp.
Xem đáp án
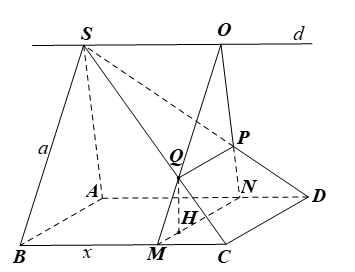
a) Trong mặt phẳng (ABCD), kẻ MN // AB // CD, N ∈ AD.
Trong mặt phẳng (SAD), kẻ đường thẳng d đi qua S và d // AD. Qua N vẽ đường thẳng song song với SA và cắt d tại O.
Nối NO cắt SD tại P và nối MO cắt SC tại Q.
Khi đó (α) chính là mặt phẳng (OMN).
Suy ra (α) ∩ (ABCD) = MN;
(α) ∩ (SBC) = MQ;
(α) ∩ (SCD) = QP;
(α) ∩ (SAD) = NP.
Câu 16:
19/07/2024Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 2a, BD = 2b; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < a), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD).
a) Xác định giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD.
Xem đáp án
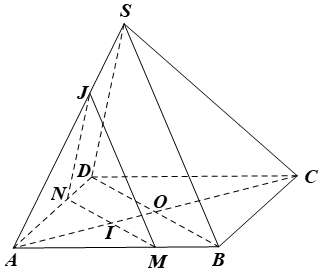
a) Trong mặt phẳng (ABCD), kẻ MN đi qua I và MN // BD (M ∈ AB, N ∈ AD).
Trong mặt phẳng (SAD), kẻ NJ // SD (J ∈ SA).
Trong mặt phẳng (SAB), nối JM.
Ta có MN // BD và BD ⊂ (SBD) nên MN // (SBD). Do đó mặt phẳng (P) chính là mặt phẳng (MNJ)
Khi đó, (P) ∩ (SAB) = JM; (P) ∩ (SAD) = JN; (P) ∩ (ABCD) = MN.
Câu 17:
06/07/2024b) Tính diện tích của hình tạo bởi các đoạn giao tuyến ở câu a theo a, b và x.
Xem đáp án
b) Các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD tạo thành tam giác MNJ.
Ta có ∆JMN ∽ ∆SBD nên ∆JMN là tam giác đều.
Ta có MN // BD, suy ra:
Câu 18:
21/07/2024Cho hình chóp S.ABCD, đáy ABCD là hình thang có đáy lớn AB và AD = a. Mặt bên SAB là tam giác cân tại S, SA = a; mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q.
a) Chứng minh MNPQ là hình thang cân.
Xem đáp án
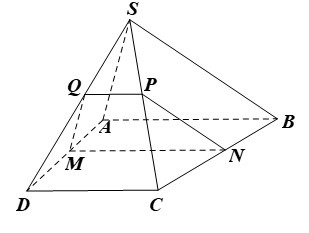
a) Ta có (ABCD) ∩ (R) = MN, (ABCD) ∩ (SAB) = AB
Mà (R) // (SAB) nên MN // AB.
Tương tự, các mặt phẳng (SAD), (SCB), (SDC) cắt hai mặt phẳng song song (R) và (SAB) theo các cặp giao tuyến song song.
Suy ra MQ // SA, NP // SB, QP // CD // AB.
Do đó QP // MN nên MNPQ là hình thang.
Ta có (hệ quả định lí Thalès) và SA = SB, suy ra MQ = NP.
Vậy MNPQ là hình thang cân.